Lesson 5
Bases and Heights of Parallelograms
Lesson Narrative
Students begin this lesson by comparing two strategies for finding the area of a parallelogram. This comparison sets the stage both for formally defining the terms base and height and for writing a general formula for the area of a parallelogram. Being able to correctly identify a base-height pair for a parallelogram requires looking for and making use of structure (MP7).
The terms base and height are potentially confusing because they are sometimes used to refer to particular line segments, and sometimes to the length of a line segment or the distance between parallel lines. Furthermore, there are always two base-height pairs for any parallelogram, so asking for the base and the height is not, technically, a well-posed question. Instead, asking for a base and its corresponding height is more appropriate. As students clarify their intended meaning when using these terms, they are attending to precision of language (MP6). In these materials, the words “base” and “height” mean the numbers unless it is clear from the context that it means a segment and that there is no potential confusion.
By the end of the lesson, students both look for a pattern they can generalize to the formula for the area of a rectangle (MP8) and make arguments that explain why this works for all parallelograms (MP3).
Learning Goals
Teacher Facing
- Comprehend the terms “base” and “height” to refer to one side of a parallelogram and the perpendicular distance between that side and the opposite side.
- Generalize (orally) a process for finding the area of a parallelogram, using the length of a base and the corresponding height.
- Identify a base and the corresponding height for a parallelogram, and understand that there are two different base-height pairs for any parallelogram.
Student Facing
Let’s investigate the area of parallelograms some more.
Required Materials
Learning Targets
Student Facing
- I can identify pairs of base and height of a parallelogram.
- I can write and explain the formula for the area of a parallelogram.
- I know what the terms "base" and "height" refer to in a parallelogram.
CCSS Standards
Addressing
Glossary Entries
-
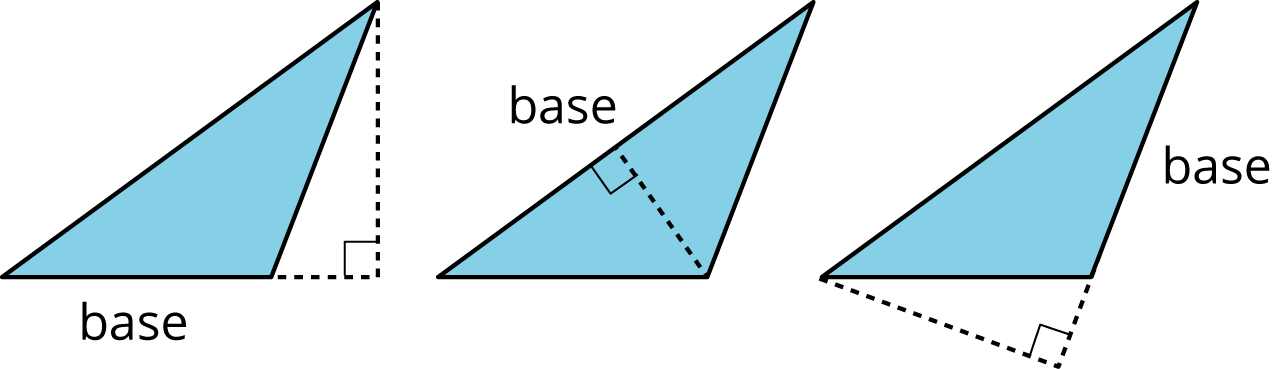
base (of a parallelogram or triangle)
We can choose any side of a parallelogram or triangle to be the shape’s base. Sometimes we use the word base to refer to the length of this side.
-
height (of a parallelogram or triangle)
The height is the shortest distance from the base of the shape to the opposite side (for a parallelogram) or opposite vertex (for a triangle).
We can show the height in more than one place, but it will always be perpendicular to the chosen base.

Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |