Lesson 5
Bases and Heights of Parallelograms
5.1: A Parallelogram and Its Rectangles (10 minutes)
Warm-up
In this warm-up, students compare and contrast two ways of decomposing and rearranging a parallelogram on a grid such that its area can be found. It serves a few purposes: to reinforce the work done in the previous lesson; to allow students to practice communicating their observations; and to shed light on the features of a parallelogram that are useful for finding area—a base and a corresponding height.
The flow of key ideas—to be uncovered during discussion and gradually throughout the lesson—is as follows:
- There are multiple ways to decompose a parallelogram (with one cut) and rearrange it into a rectangle whose area we can determine.
- The cut can be made in different places, but to compose a rectangle, the cut has to be at a right angle to two opposite sides of the parallelogram.
- The length of one side of this newly composed rectangle is the same as the length of one side of the parallelogram. We use the term base to refer to this side.
- The length of the other side of the rectangle is the length of the cut we made to the parallelogram. We call this segment a height that corresponds to the chosen base.
- We use these two lengths to determine the area of the rectangle, and thus also the area of the parallelogram.
As students work and discuss, identify those who make comparisons in terms of the first two points so they could share later. Be sure to leave enough time to discuss the first four points as a class.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet think time and access to geometry toolkits. Ask them to share their responses with a partner afterwards.
If using the digital activity, have students explore the applet for 3 minutes individually, and then discuss with a partner. Students will be able to see the cuts by dragging the point on the segment under the parallelogram.
Student Facing
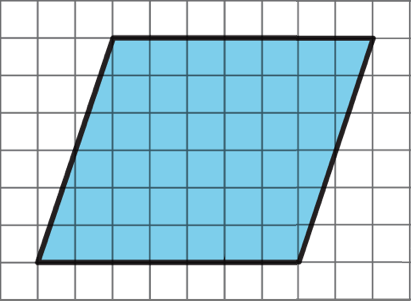
Elena and Tyler were finding the area of this parallelogram:

Move the slider to see how Tyler did it:
Move the slider to see how Elena did it:
How are the two strategies for finding the area of a parallelogram the same? How they are different?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet think time and access to geometry toolkits. Ask them to share their responses with a partner afterwards.
If using the digital activity, have students explore the applet for 3 minutes individually, and then discuss with a partner. Students will be able to see the cuts by dragging the point on the segment under the parallelogram.
Student Facing
Elena and Tyler were finding the area of this parallelogram:
Here is how Elena did it:
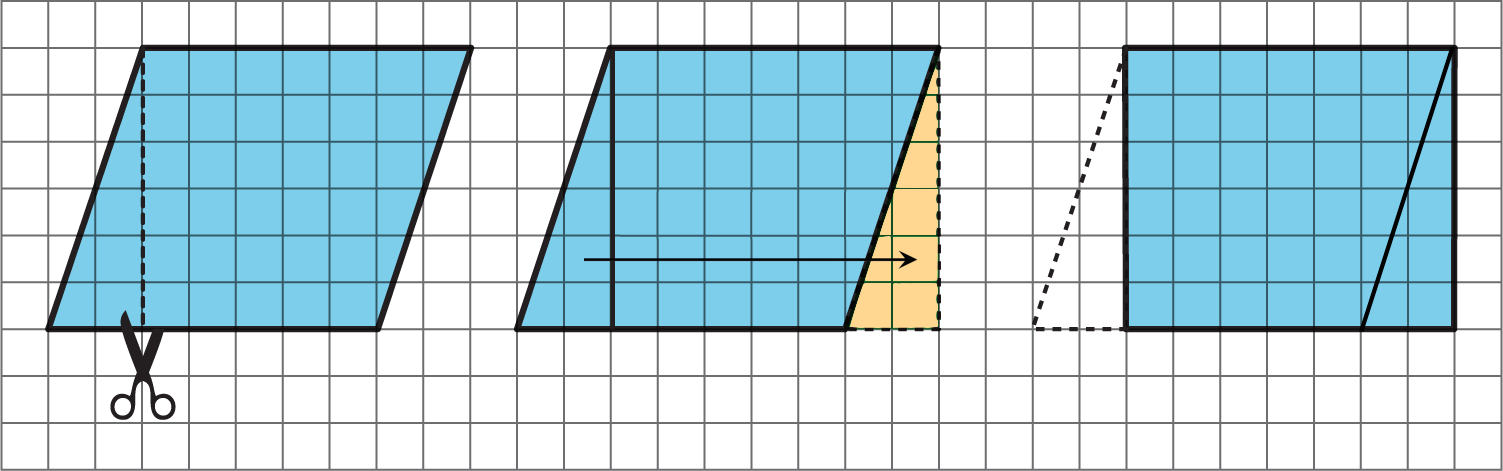
Here is how Tyler did it:
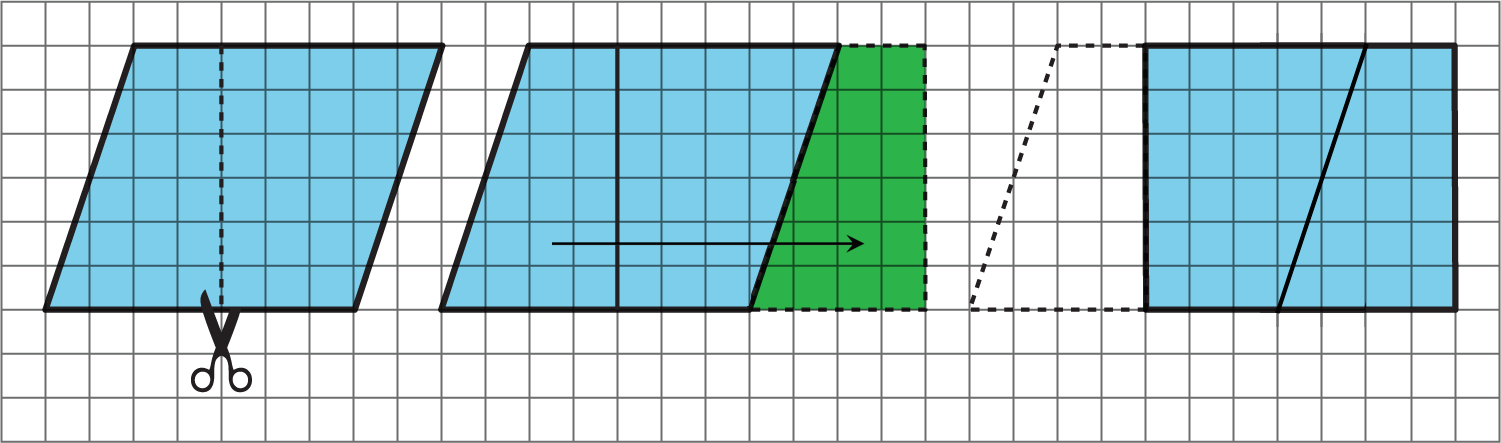
How are the two strategies for finding the area of a parallelogram the same? How they are different?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask a few students to share what was the same and what was different about the methods they observed.
Highlight the following points on how Elena and Tyler's approaches are the same, though do not expect students to use the language. Instead, rely on pointing and gesturing to make clear what is meant. If any of these are not mentioned by the students, share them.
- The rectangles are identical; they have the same side lengths. (Label the side lengths of the rectangles.)
- The cuts were made in different places, but the length of the cuts was the same. (Label the lengths along the vertical cuts.)
- The horizontal sides of the parallelogram have the same length as the horizontal sides of the rectangle. (Point out how both segments have the same length.)
- The length of each cut is also the distance between the two horizontal sides of the parallelogram. It is also the vertical side length of the rectangle. (Point out how that distance stays the same across the horizontal length of the parallelogram.)
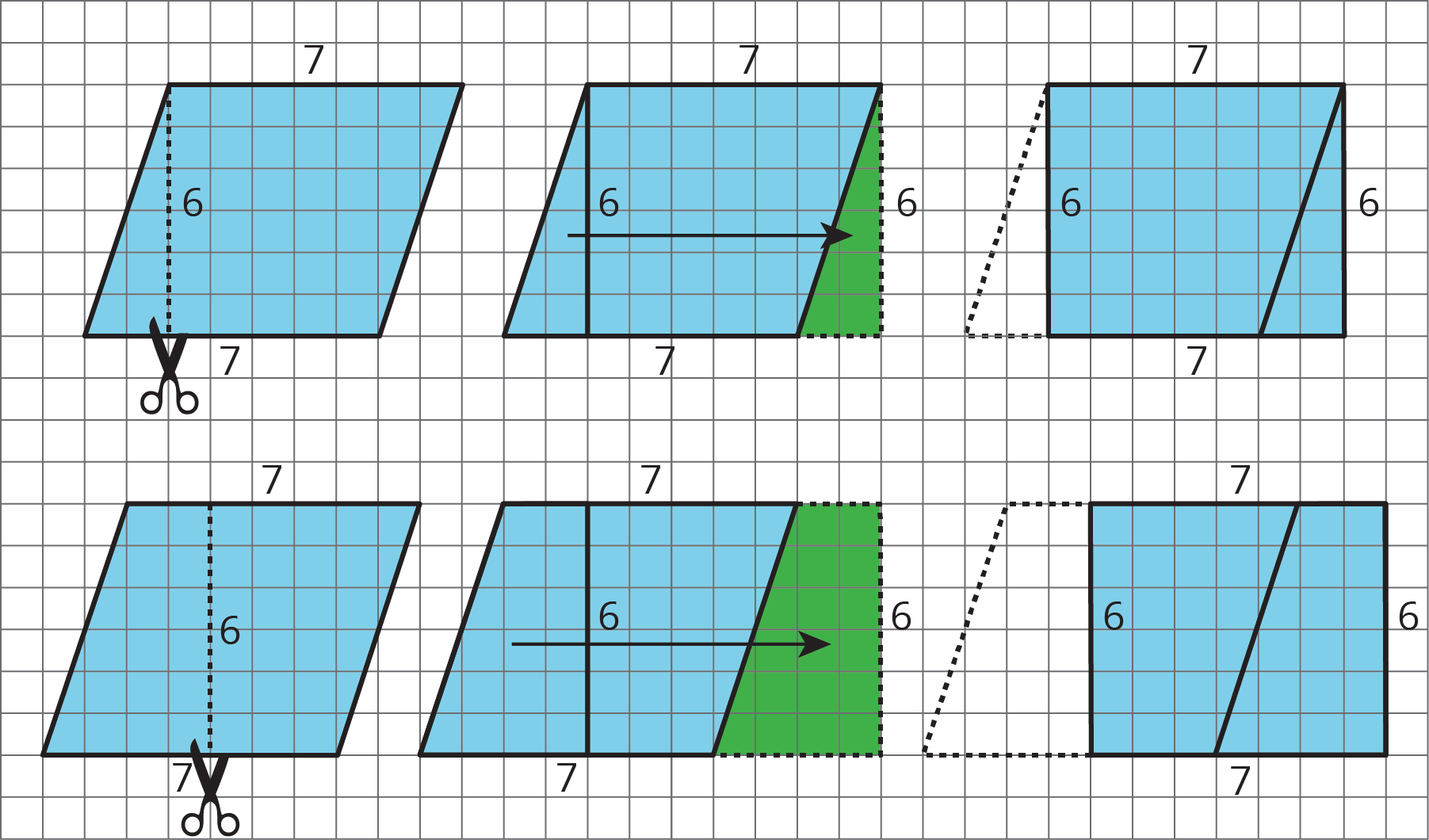
Begin to connect the observations to the terms base and height. For example, explain:
- “The two measurements that we see here have special names. The length of one side of the parallelogram—which is also the length of one side of the rectangle—is called a base. The length of the vertical cut segment—which is also the length of the vertical side of the rectangle—is called a height that corresponds to that base.”
- “Here, the side of the parallelogram that is 7 units long is also called a base. In other words, the word base is used for both the segment and the measurement.”
Tell students that we will explore bases and heights of a parallelogram in this lesson.
5.2: The Right Height? (20 minutes)
Activity
Previously, students saw numerical examples of a base and a height of a parallelogram. This activity further develops the idea of base and height through examples and non-examples and error analysis.
Some important ideas to be uncovered here:
- In a parallelogram, the term "base" refers to the length of one side and "height" to the length of a perpendicular segment between that side and the opposite side.
- Any side of a parallelogram can be a base.
- There are always two base-height pairs for a given parallelogram.
Launch
Display the image of examples and non-examples of bases and heights for all to see. Read aloud the description for examples and non-examples. Give students a minute to observe it and to prepare to share at least one thing they notice and one thing they wonder about. When the minute is up, invite students to share their responses with the class, and record these for all to see. It isn't necessary to address their questions at this time.
Students may notice:
- Both sets of diagrams show the same 2 pairs of parallelograms and the same sides labeled “base.”
- All the examples show a right-angle mark, a dashed segment, and a side labeled “base.”
- Only one of the non-examples show a right-angle mark, but all of them show a dashed segment.
- In both examples and non-examples, there is one parallelogram with a dashed segment and a right angle shown outside of it.
- If the dashed segments are used to cut the first three parallelograms in the examples, the cut-out pieces could be rearranged to form a rectangle. The same cannot be done for the dashed segments in the non-examples.
They may wonder:
- why some dashed segments are inside the parallelogram and some are outside.
- what the rule might be for a dashed segment to be considered a height.
- what the bases and heights have to do with area.
Arrange students in groups of 2. Give students 4–5 minutes to complete the first question with their partner. Ask them to pause for a class discussion after the first question. Select a student or a group to make a case for whether each statement is true or false. If one or more students disagree, ask them to explain their reasoning and discuss to reach a consensus. Before moving on to the next question, be sure students record the verified true statements so that they can be used as a reference later.
Give students 3–4 minutes of quiet time to answer the second question and another 2–3 minutes to share their responses with a partner. Ask them to focus partner conversations on the following questions, displayed for all to see:
- How do you know the parallelogram is labeled correctly or incorrectly?
- Is there another way a base and height could be labeled on this parallelogram?
After answering the questions, students using the digital activity can explore the applet https://ggbm.at/UnfbrN96 and use it to verify their responses and further their understanding of bases and heights. The applet is a dynamic parallelogram with a height displayed. It allows students to see placements of height in a variety of parallelograms and when any side is chosen as a base.
Design Principle(s): Support sense-making
Student Facing
Study the examples and non-examples of bases and heights of parallelograms.
- Examples: The dashed segments in these drawings represent the corresponding height for the given base.

- Non-examples: The dashed segments in these drawings do not represent the corresponding height for the given base.
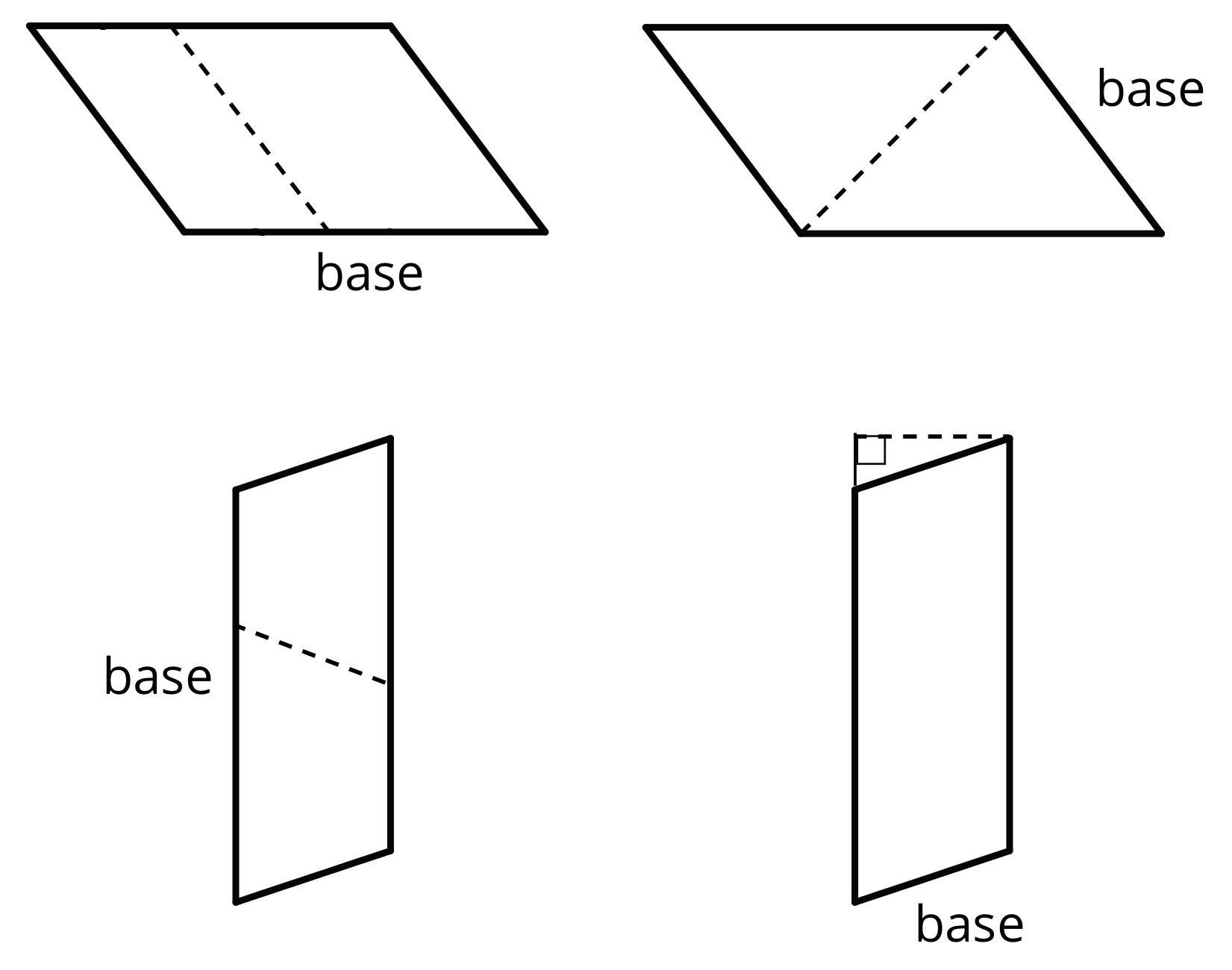
-
Select all the statements that are true about bases and heights in a parallelogram.
- Only a horizontal side of a parallelogram can be a base.
- Any side of a parallelogram can be a base.
- A height can be drawn at any angle to the side chosen as the base.
- A base and its corresponding height must be perpendicular to each other.
- A height can only be drawn inside a parallelogram.
- A height can be drawn outside of the parallelogram, as long as it is drawn at a 90-degree angle to the base.
- A base cannot be extended to meet a height.
- Five students labeled a base \(b\) and a corresponding height \(h\) for each of these parallelograms. Are all drawings correctly labeled? Explain how you know.
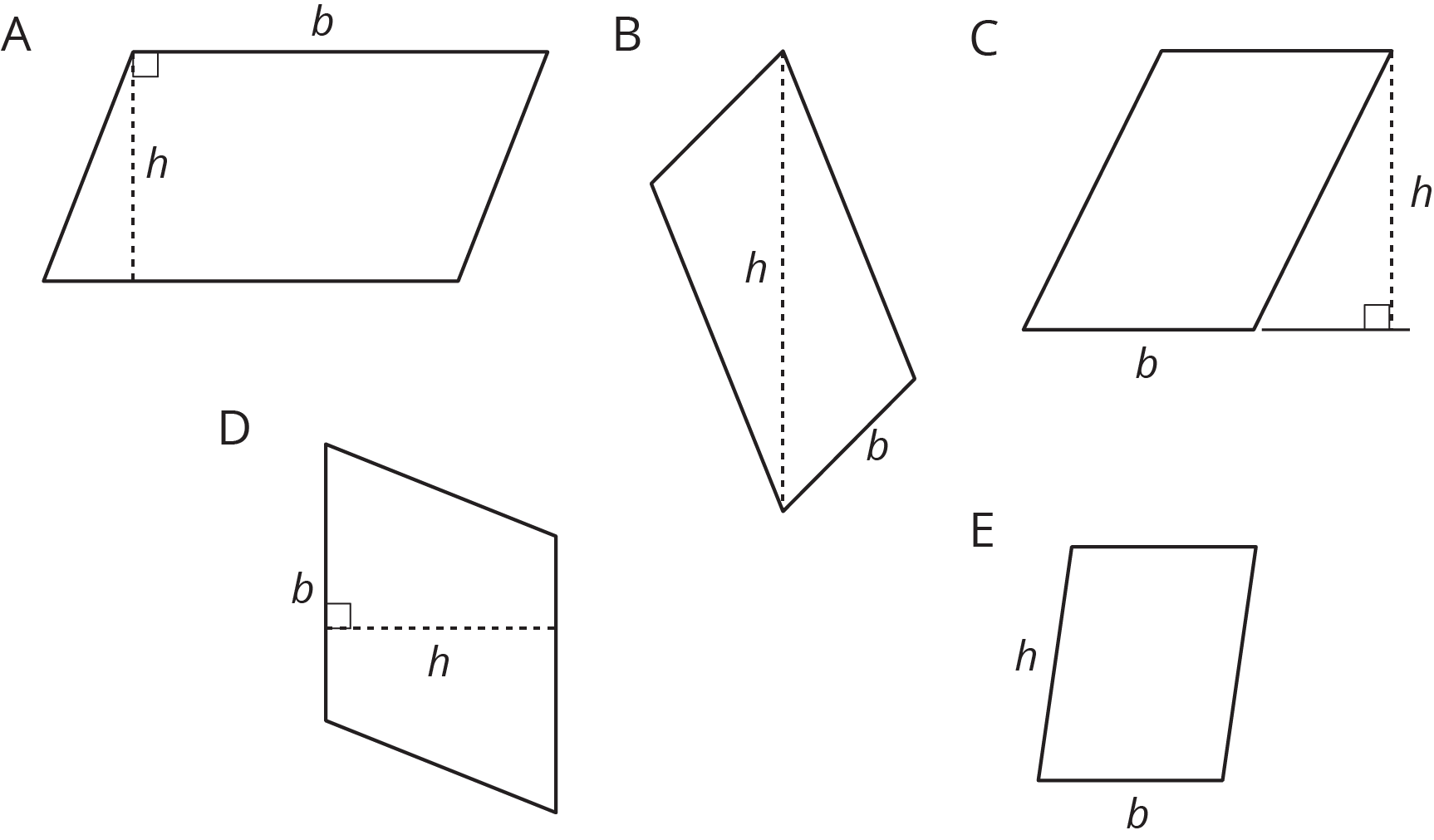
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
In the applet, the parallelogram is made of solid line segments, and the height and supporting lines are made of dashed line segments. A base b and corresponding height h are labeled.
Experiment with dragging all of the movable points around the screen. Can you change the parallelogram so that . . .
its height is in a different location?
it has horizontal sides?
it is tall and skinny?
it is also a rectangle?
it is not a rectangle, and has b=5 and h=3?
Launch
Display the image of examples and non-examples of bases and heights for all to see. Read aloud the description for examples and non-examples. Give students a minute to observe it and to prepare to share at least one thing they notice and one thing they wonder about. When the minute is up, invite students to share their responses with the class, and record these for all to see. It isn't necessary to address their questions at this time.
Students may notice:
- Both sets of diagrams show the same 2 pairs of parallelograms and the same sides labeled “base.”
- All the examples show a right-angle mark, a dashed segment, and a side labeled “base.”
- Only one of the non-examples show a right-angle mark, but all of them show a dashed segment.
- In both examples and non-examples, there is one parallelogram with a dashed segment and a right angle shown outside of it.
- If the dashed segments are used to cut the first three parallelograms in the examples, the cut-out pieces could be rearranged to form a rectangle. The same cannot be done for the dashed segments in the non-examples.
They may wonder:
- why some dashed segments are inside the parallelogram and some are outside.
- what the rule might be for a dashed segment to be considered a height.
- what the bases and heights have to do with area.
Arrange students in groups of 2. Give students 4–5 minutes to complete the first question with their partner. Ask them to pause for a class discussion after the first question. Select a student or a group to make a case for whether each statement is true or false. If one or more students disagree, ask them to explain their reasoning and discuss to reach a consensus. Before moving on to the next question, be sure students record the verified true statements so that they can be used as a reference later.
Give students 3–4 minutes of quiet time to answer the second question and another 2–3 minutes to share their responses with a partner. Ask them to focus partner conversations on the following questions, displayed for all to see:
- How do you know the parallelogram is labeled correctly or incorrectly?
- Is there another way a base and height could be labeled on this parallelogram?
After answering the questions, students using the digital activity can explore the applet ggbm.at/UnfbrN96 and use it to verify their responses and further their understanding of bases and heights. The applet is a dynamic parallelogram with a height displayed. It allows students to see placements of height in a variety of parallelograms and when any side is chosen as a base.
Design Principle(s): Support sense-making
Student Facing
Study the examples and non-examples of bases and heights of parallelograms.
-
Examples: The dashed segments in these drawings represent the corresponding height for the given base.

-
Non-examples: The dashed segments in these drawings do not represent the corresponding height for the given base.

-
Select all the statements that are true about bases and heights in a parallelogram.
- Only a horizontal side of a parallelogram can be a base.
- Any side of a parallelogram can be a base.
- A height can be drawn at any angle to the side chosen as the base.
- A base and its corresponding height must be perpendicular to each other.
- A height can only be drawn inside a parallelogram.
- A height can be drawn outside of the parallelogram, as long as it is drawn at a 90-degree angle to the base.
- A base cannot be extended to meet a height.
- Five students labeled a base \(b\) and a corresponding height \(h\) for each of these parallelograms. Are all drawings correctly labeled? Explain how you know.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not yet internalize that any side of parallelogram can be a base (they may think that a base must be the bottom, horizontal side), or that the height needs to be perpendicular to the base. Point out where the right angle symbols are located and how they relate to the height. Students may think a segment showing the height cannot be drawn outside of the parallelogram (as in Parallelogram C).
Students may relate how they think about the side lengths of a rectangle and inaccurately apply it to Parallelogram E.
Activity Synthesis
Poll the class—with a quick agree-or-disagree signal—on whether each figure in the last question is labeled correctly with \(b\) and \(h\). After each polling, ask a student to explain how they know it is correct or incorrect.
If a parallelogram is incorrectly labeled, ask where a correct height could be. If it is correctly labeled, ask students if there is another base and height that could be labeled on this parallelogram. Be sure students understand which parallelograms are labeled correctly before moving forward in this lesson.
An important point to emphasize: “We can choose any side of a parallelogram as a base. To find the height that corresponds to that base, draw a segment that joins the base and its opposite side; that segment has to be perpendicular to both.”
Consider using the applet ggbm.at/UnfbrN96 to further illustrate possible base-height pairs and reinforce students' understanding of them.
5.3: Finding the Formula for Area of Parallelograms (15 minutes)
Activity
In previous lessons, students reasoned about the area of parallelograms by decomposing, rearranging, and enclosing them and by using what they know about the area of rectangles. They also identified base-height pairs in parallelograms. Here, they use what they learned to find the area of new parallelograms, generalize the process, and write an expression for finding the area of any parallelogram.
As students discuss their work, monitor conversations for any disagreements between partners. Support them by asking clarifying questions:
- “How did you choose a base? How can you be sure that is the height?”
- “How did you find the area? Why did you choose that strategy for this parallelogram?”
- “Is there another way to find the area and to check our answer?”
Launch
Keep students in groups of 2. Give students access to their geometry toolkits and 5–7 minutes of quiet think time to complete the first four rows of the table. Ask them to be prepared to share their reasoning. If time is limited, consider splitting up the work: have one partner work independently on parallelograms A and C, and the other partner on B and D. Encourage students to use their work from earlier activities (on bases and heights) as a reference.
Ask students to pause after completing the first four rows and to share their responses with their partner. Then, they should discuss how to write the expression for the area of any parallelogram. Students should notice that the area of every parallelogram is the product of a base and its corresponding height.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
For each parallelogram:
- Identify a base and a corresponding height, and record their lengths in the table.
- Find the area of the parallelogram and record it in the last column of the table.
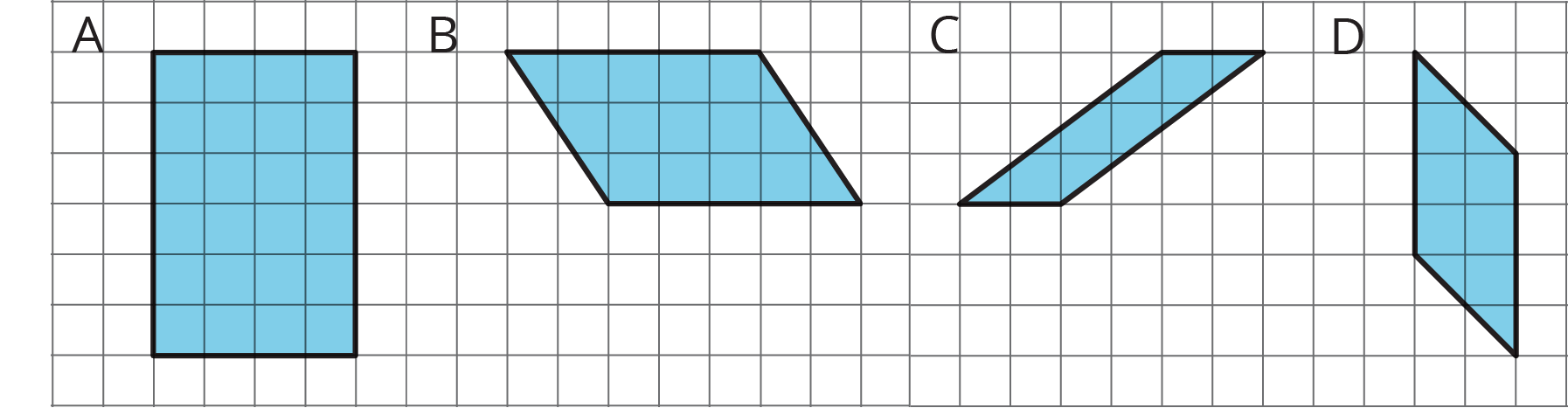
| parallelogram | base (units) | height (units) | area (sq units) |
| A | |||
| B | |||
| C | |||
| D | |||
| any parallelogram | \(b\) | \(h\) |
In the last row, write an expression for the area of any parallelogram, using \(b\) and \(h\) .
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- What happens to the area of a parallelogram if the height doubles but the base is unchanged? If the height triples? If the height is 100 times the original?
- What happens to the area if both the base and the height double? Both triple? Both are 100 times their original lengths?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Finding a height segment outside of the parallelogram may still be a rather unfamiliar idea to students. Have examples from the “The Right Height?” section visible so they can serve as a reference in finding heights.
Students may say that the base of Parallelogram D cannot be determined because, as displayed, it does not have a horizontal side. Remind students that in an earlier activity we learned that any side of a parallelogram could be a base. Ask students to see if there is a side whose length can be determined.
Activity Synthesis
Display the parallelograms and the table for all to see. Select a few students to share the correct answers for each parallelogram. As students share, highlight the base-height pairs on each parallelogram and record the responses in the table. Although only one base-height pair is named for each parallelogram, reiterate that there is another pair. Show the second pair on the diagram or ask students to point it out.
After all answers for the first four rows are shared, discuss the following questions, displayed for all to see:
- “How did you determine the expression for the area for any parallelogram?” (The areas of parallelograms A–D are each the product of base and height.)
- “Suppose you decompose a parallelogram with a cut and rearrange it into a rectangle. Does this expression for finding area still work? Why or why not?” (Yes. One side of the rectangle will be the same as the base of the parallelogram. The height of the parallelogram is also the height of the rectangle—both are perpendicular to the base.)
- “Do you think this expression will always work?”
Be sure everyone has the correct expression for finding the area of a parallelogram by the end of the discussion. The second discussion question is meant to elicit connections to the parallelogram’s related rectangle as they decomposed and rearranged to find the area. The third question (about whether the expression will always work) is not meant to be proven here, so speculation on students’ part is expected at this point. It is intended to prompt students to think of other differently-shaped parallelograms beyond the four shown here.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
In this lesson, we identified a base and a corresponding height in a parallelogram, and then wrote an algebraic expression for finding the area of any parallelogram.
- “How do you decide the base of a parallelogram?” (Any side can be a base. Sometimes one side is preferable over another because its length is known or easy to know.)
- “Once we have chosen a base, how can we identify a height that corresponds to it?” (Identify a perpendicular segment that connects that base and the opposite side; find the length of that segment.)
- “In how many ways can we identify a base and a height for a given parallelogram?” (There are two possible bases. For each base, many possible segments can represent the corresponding height.)
- “What is the relationship between the base and height of a parallelogram and its area?” (The area is the product of base and height.)
5.4: Cool-down - Parallelograms S and T (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
- We can choose any of the four sides of a parallelogram as the base. Both the side (the segment) and its length (the measurement) are called the base.
-
If we draw any perpendicular segment from a point on the base to the opposite side of the parallelogram, that segment will always have the same length. We call that value the height. There are infinitely many segments that can represent the height!
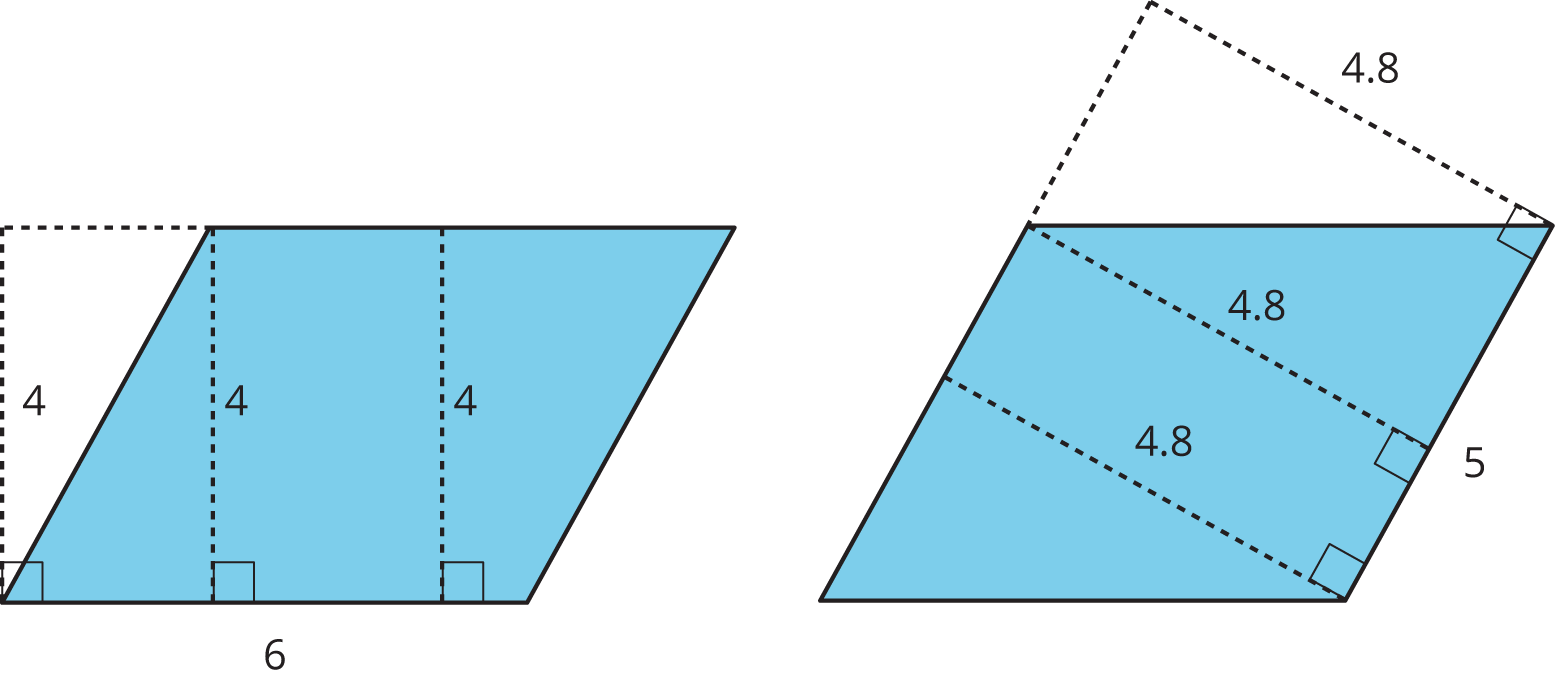
Here are two copies of the same parallelogram. On the left, the side that is the base is 6 units long. Its corresponding height is 4 units. On the right, the side that is the base is 5 units long. Its corresponding height is 4.8 units. For both, three different segments are shown to represent the height. We could draw in many more!
No matter which side is chosen as the base, the area of the parallelogram is the product of that base and its corresponding height. We can check this:
\(4 \times 6 = 24\)
and
\(4.8 \times 5 = 24\)
We can see why this is true by decomposing and rearranging the parallelograms into rectangles.

Notice that the side lengths of each rectangle are the base and height of the parallelogram. Even though the two rectangles have different side lengths, the products of the side lengths are equal, so they have the same area! And both rectangles have the same area as the parallelogram.
We often use letters to stand for numbers. If \(b\) is base of a parallelogram (in units), and \(h\) is the corresponding height (in units), then the area of the parallelogram (in square units) is the product of these two numbers. \(\displaystyle b \boldcdot h\)
Notice that we write the multiplication symbol with a small dot instead of a \(\times\) symbol. This is so that we don’t get confused about whether \(\times\) means multiply, or whether the letter \(x\) is standing in for a number.
In high school, you will be able to prove that a perpendicular segment from a point on one side of a parallelogram to the opposite side will always have the same length.
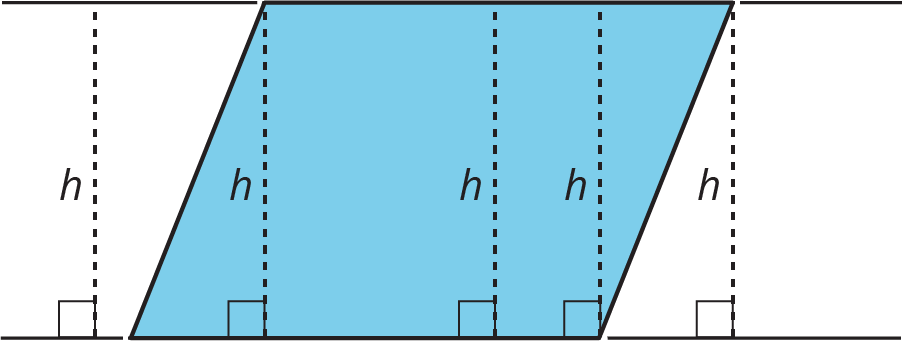
You can see this most easily when you draw a parallelogram on graph paper. For now, we will just use this as a fact.