Lesson 5
Bases and Heights of Parallelograms
Let’s investigate the area of parallelograms some more.
5.1: A Parallelogram and Its Rectangles
Elena and Tyler were finding the area of this parallelogram:
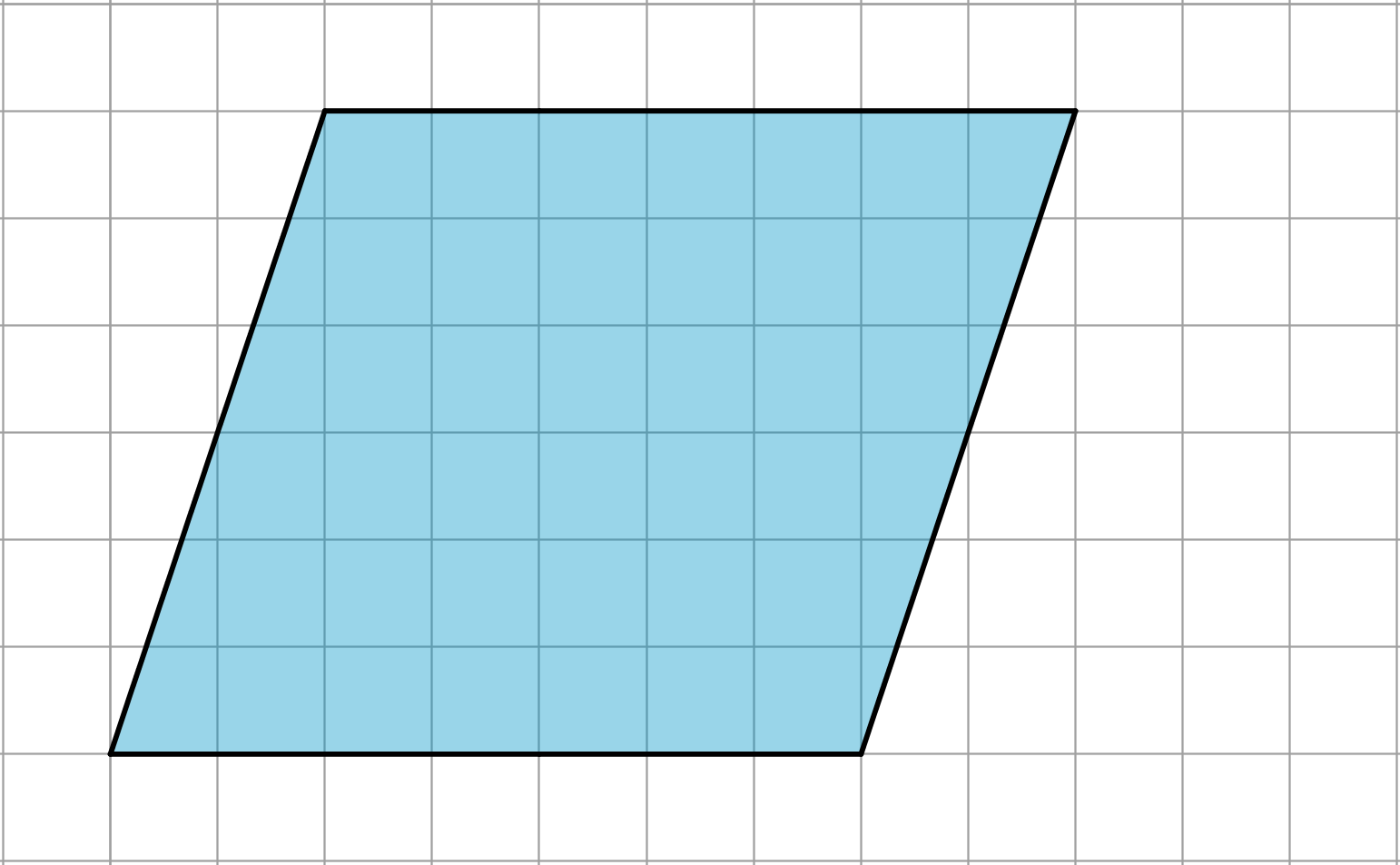
Move the slider to see how Tyler did it:
Move the slider to see how Elena did it:
How are the two strategies for finding the area of a parallelogram the same? How they are different?
5.2: The Right Height?
Study the examples and non-examples of bases and heights of parallelograms.
- Examples: The dashed segments in these drawings represent the corresponding height for the given base.

- Non-examples: The dashed segments in these drawings do not represent the corresponding height for the given base.
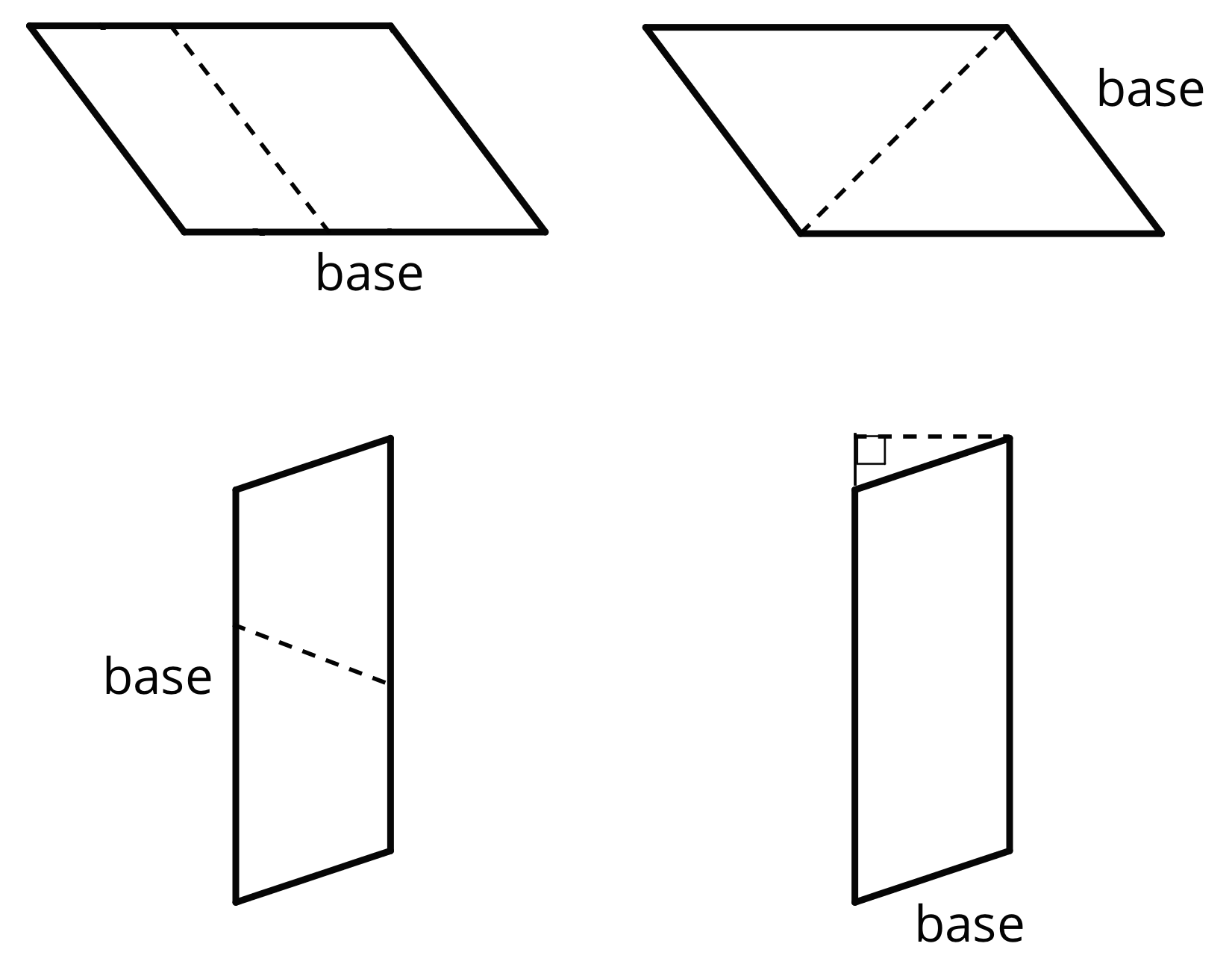
-
Select all the statements that are true about bases and heights in a parallelogram.
- Only a horizontal side of a parallelogram can be a base.
- Any side of a parallelogram can be a base.
- A height can be drawn at any angle to the side chosen as the base.
- A base and its corresponding height must be perpendicular to each other.
- A height can only be drawn inside a parallelogram.
- A height can be drawn outside of the parallelogram, as long as it is drawn at a 90-degree angle to the base.
- A base cannot be extended to meet a height.
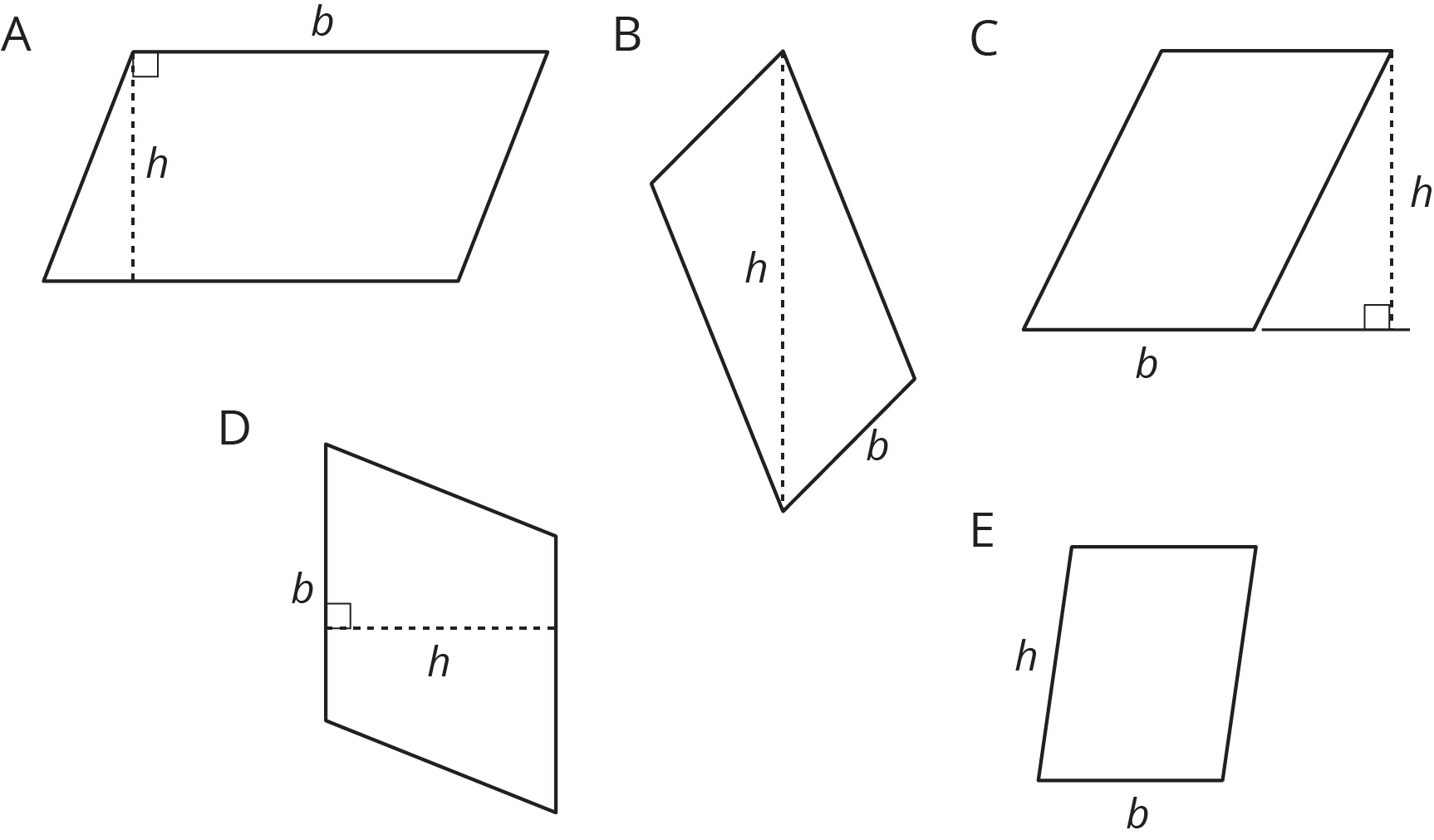
- Five students labeled a base \(b\) and a corresponding height \(h\) for each of these parallelograms. Are all drawings correctly labeled? Explain how you know.
In the applet, the parallelogram is made of solid line segments, and the height and supporting lines are made of dashed line segments. A base b and corresponding height h are labeled.
Experiment with dragging all of the movable points around the screen. Can you change the parallelogram so that . . .
its height is in a different location?
it has horizontal sides?
it is tall and skinny?
it is also a rectangle?
it is not a rectangle, and has b=5 and h=3?
5.3: Finding the Formula for Area of Parallelograms
For each parallelogram:
- Identify a base and a corresponding height, and record their lengths in the table.
- Find the area of the parallelogram and record it in the last column of the table.
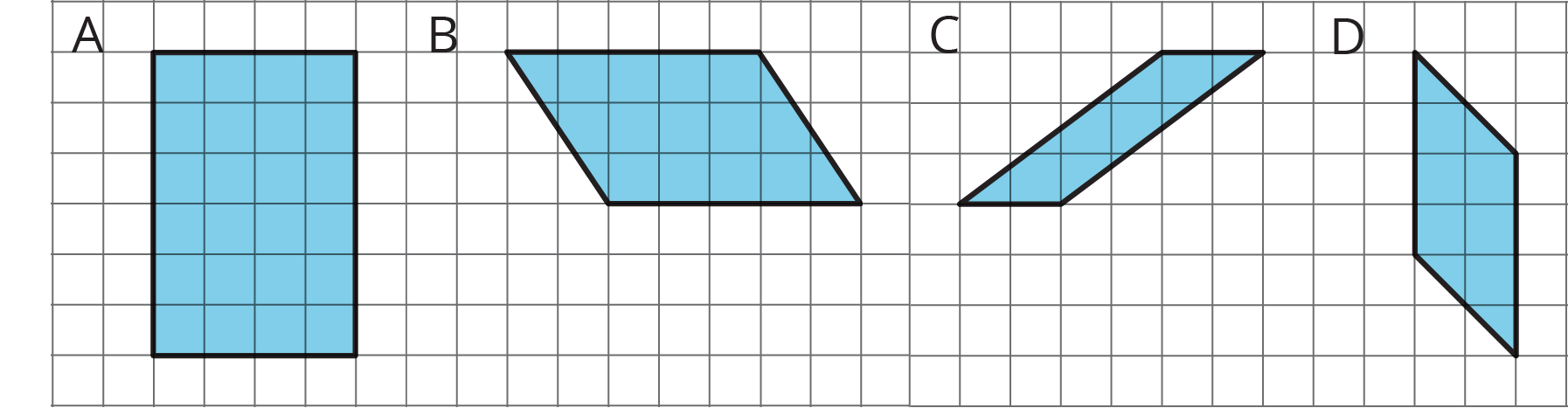
| parallelogram | base (units) | height (units) | area (sq units) |
| A | |||
| B | |||
| C | |||
| D | |||
| any parallelogram | \(b\) | \(h\) |
In the last row, write an expression for the area of any parallelogram, using \(b\) and \(h\) .
- What happens to the area of a parallelogram if the height doubles but the base is unchanged? If the height triples? If the height is 100 times the original?
- What happens to the area if both the base and the height double? Both triple? Both are 100 times their original lengths?
Summary
- We can choose any of the four sides of a parallelogram as the base. Both the side (the segment) and its length (the measurement) are called the base.
-
If we draw any perpendicular segment from a point on the base to the opposite side of the parallelogram, that segment will always have the same length. We call that value the height. There are infinitely many segments that can represent the height!
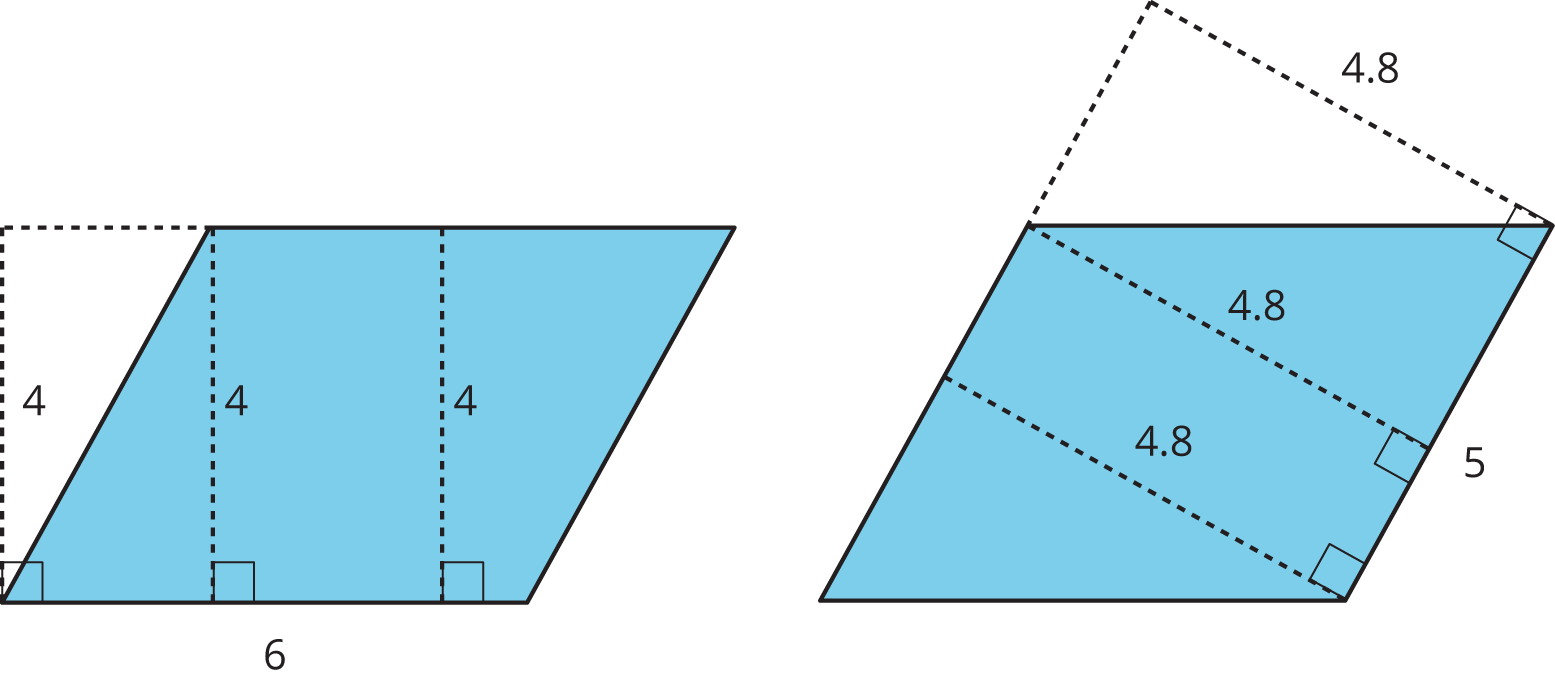
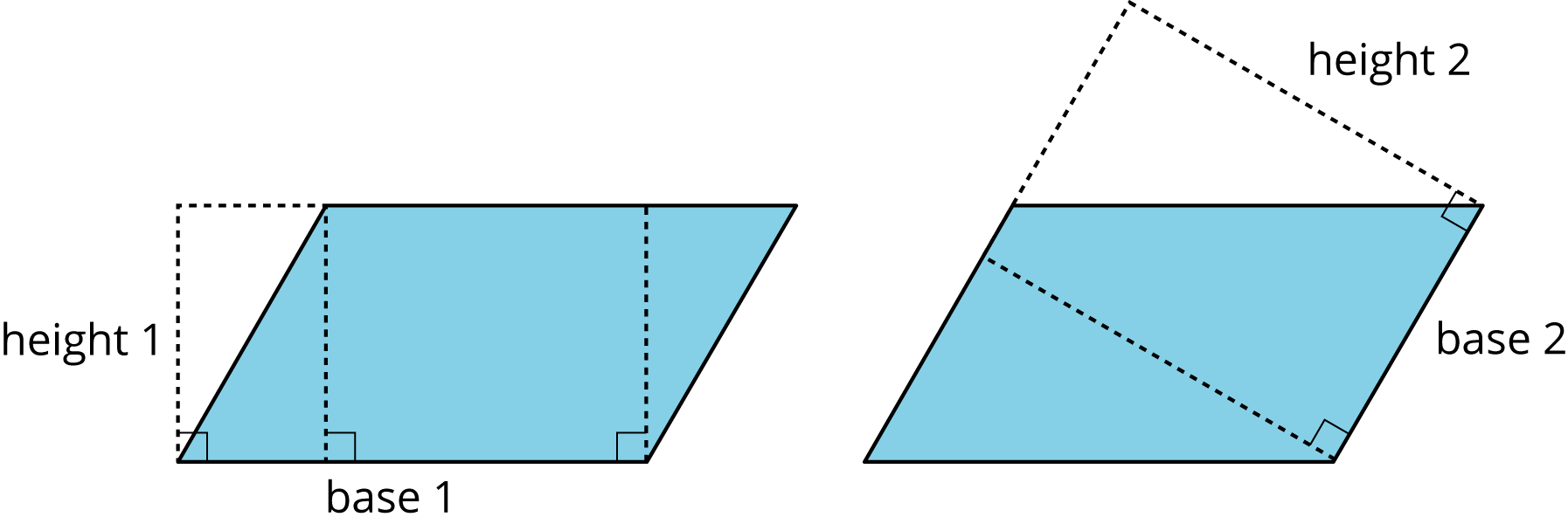
Here are two copies of the same parallelogram. On the left, the side that is the base is 6 units long. Its corresponding height is 4 units. On the right, the side that is the base is 5 units long. Its corresponding height is 4.8 units. For both, three different segments are shown to represent the height. We could draw in many more!
No matter which side is chosen as the base, the area of the parallelogram is the product of that base and its corresponding height. We can check this:
\(4 \times 6 = 24\)
and
\(4.8 \times 5 = 24\)
We can see why this is true by decomposing and rearranging the parallelograms into rectangles.
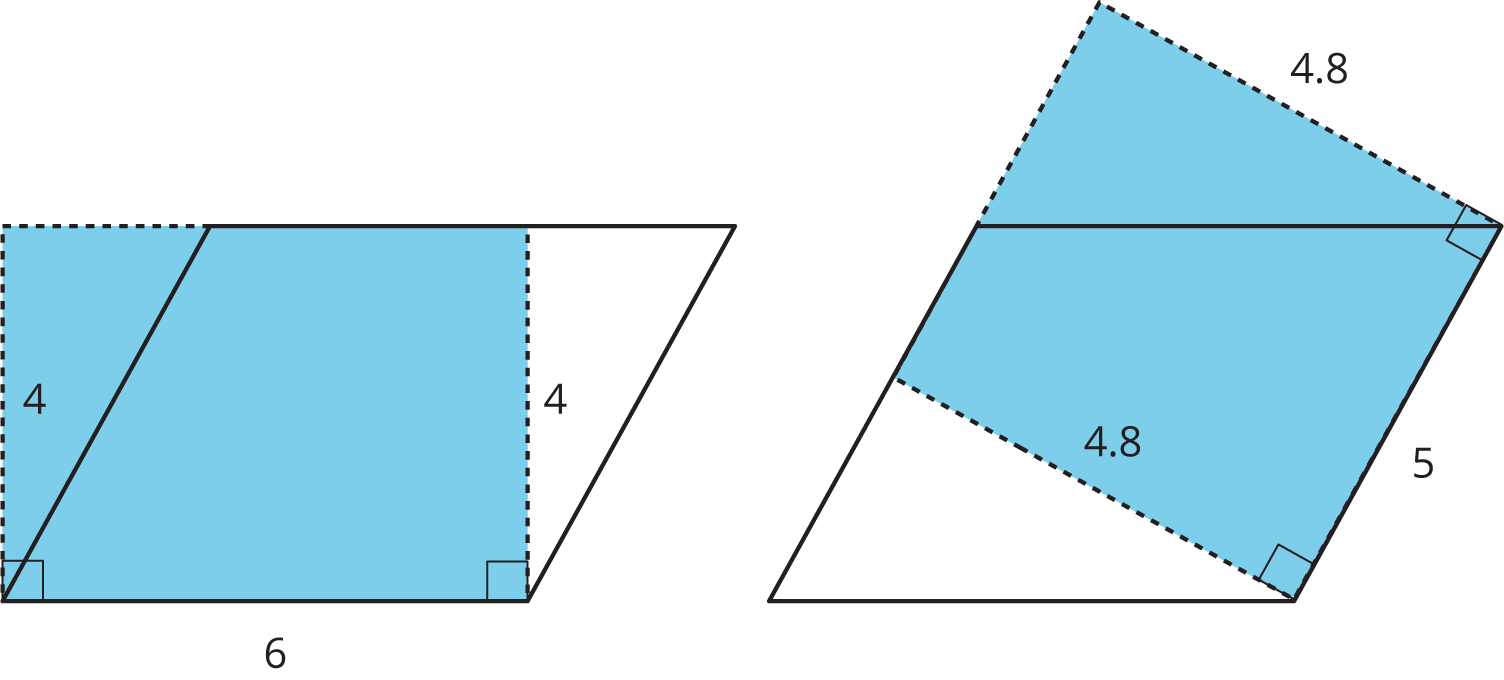
Notice that the side lengths of each rectangle are the base and height of the parallelogram. Even though the two rectangles have different side lengths, the products of the side lengths are equal, so they have the same area! And both rectangles have the same area as the parallelogram.
We often use letters to stand for numbers. If \(b\) is base of a parallelogram (in units), and \(h\) is the corresponding height (in units), then the area of the parallelogram (in square units) is the product of these two numbers. \(\displaystyle b \boldcdot h\)
Notice that we write the multiplication symbol with a small dot instead of a \(\times\) symbol. This is so that we don’t get confused about whether \(\times\) means multiply, or whether the letter \(x\) is standing in for a number.
In high school, you will be able to prove that a perpendicular segment from a point on one side of a parallelogram to the opposite side will always have the same length.
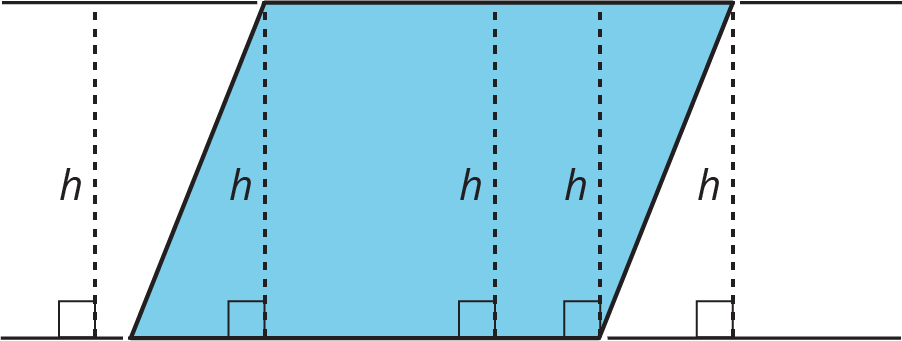
You can see this most easily when you draw a parallelogram on graph paper. For now, we will just use this as a fact.
Glossary Entries
- base (of a parallelogram or triangle)
We can choose any side of a parallelogram or triangle to be the shape’s base. Sometimes we use the word base to refer to the length of this side.
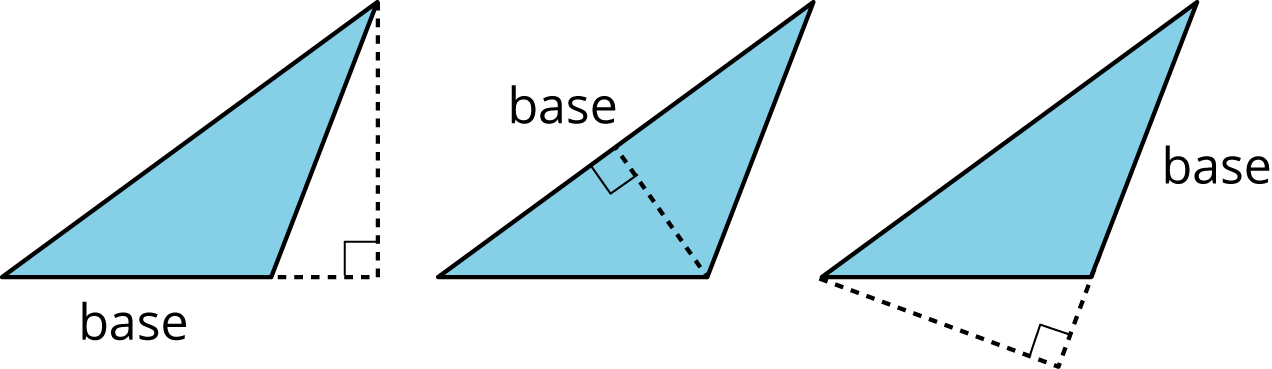
- height (of a parallelogram or triangle)
The height is the shortest distance from the base of the shape to the opposite side (for a parallelogram) or opposite vertex (for a triangle).
We can show the height in more than one place, but it will always be perpendicular to the chosen base.
- parallelogram
A parallelogram is a type of quadrilateral that has two pairs of parallel sides.
Here are two examples of parallelograms.

- quadrilateral
A quadrilateral is a type of polygon that has 4 sides. A rectangle is an example of a quadrilateral. A pentagon is not a quadrilateral, because it has 5 sides.