Lesson 3
Reasoning to Find Area
3.1: Comparing Regions (5 minutes)
Warm-up
This activity prompts students to use reasoning strategies from earlier lessons to compare the areas of two figures. It is also an opportunity to use (or introduce) tracing paper as a way to illustrate decomposing and rearranging a figure.
As students work, look for students who are able to explain or show how they know that the areas are equal. Some students may simply look at the figures and say, with no justification, that they have the same area. Urge them to think of a way to show that their conclusion is true.
Launch
Give students access to their geometry toolkits, and allow for 2 minutes of quiet think time. Ask them to be ready to support their answer, and remind them to use the tools at their disposal. Have copies of the blackline master ready for students who propose cutting the figures out for comparison or as a way to differentiate the activity.
Student Facing
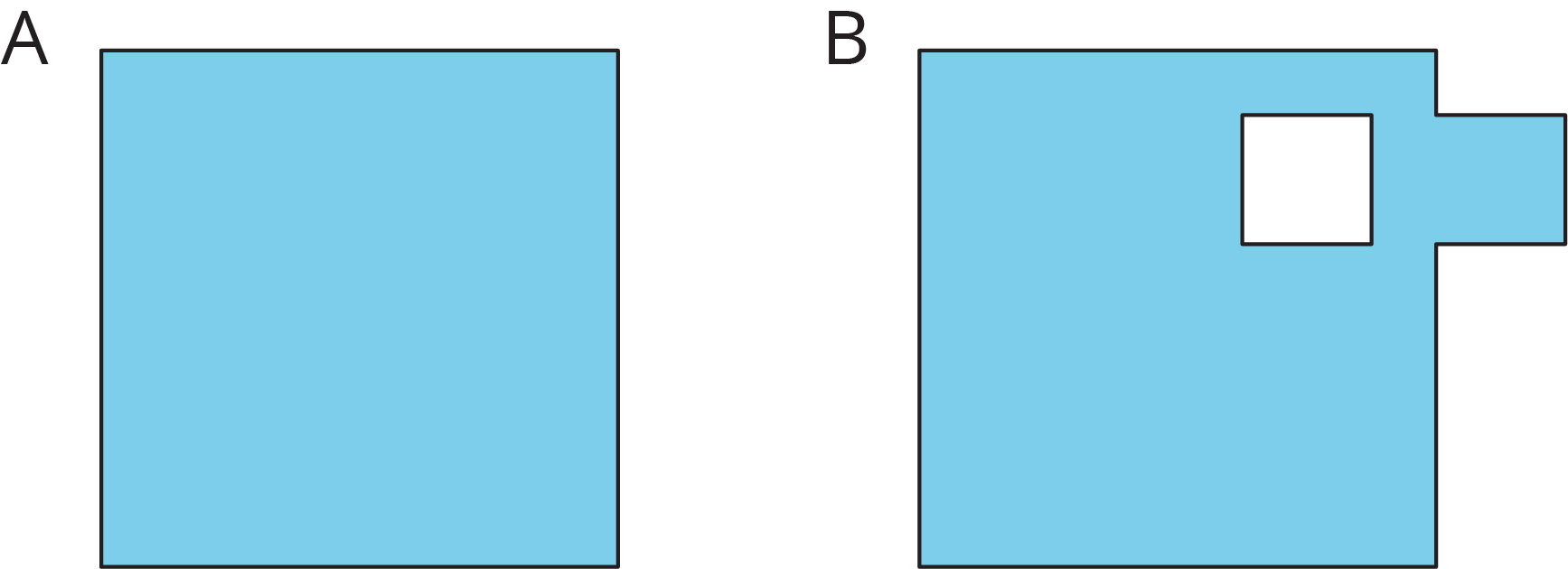
Is the area of Figure A greater than, less than, or equal to the area of the shaded region in Figure B? Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may interpret the area of Figure B as the entire region inside the outer boundary including the unfilled square. Clarify that we want to compare the areas of only the shaded parts of Figure B and Figure A.
Activity Synthesis
Start the discussion by asking the students to indicate which of the three possible responses—area of Figure A is greater, area of Figure B is greater, or the areas are equal—they choose.
Select previously identified students to share their explanations. If no student mentioned using tracing paper, demonstrate the following.
- Decomposing and rearranging Figure B: Place a piece of tracing paper over Figure B. Draw the boundary of the small square, making a dotted auxiliary line to show its separation from the large square. Move the tracing paper so that the boundary of the small square matches up exactly with the boundary of the square-shaped hole in Figure B. Draw the boundary of the large square. Explain that the small square matches up exactly with the hole, so we know the small, shaded square and the hole have equal area.
- Matching the two figures: Move the tracing paper over Figure A so that the boundary of the rearranged Figure B matches up exactly with that of Figure A. Say, “When two figures that are overlaid one on top of another match up exactly, their areas are equal.”
Highlight the strategies and principles that are central to this unit. Tell students, “We just decomposed and rearranged Figure B so that it matches up exactly with Figure A. When two figures that are overlaid one on top of another match up exactly, we can say that their areas are equal.”
3.2: On the Grid (20 minutes)
Activity
This activity gives students opportunities to find areas of regions using a variety of strategies. When working with a grid, students may start by counting squares, as they had done in earlier grades. However, the figures have been chosen to elicit the strategies listed in the Lesson Narrative.
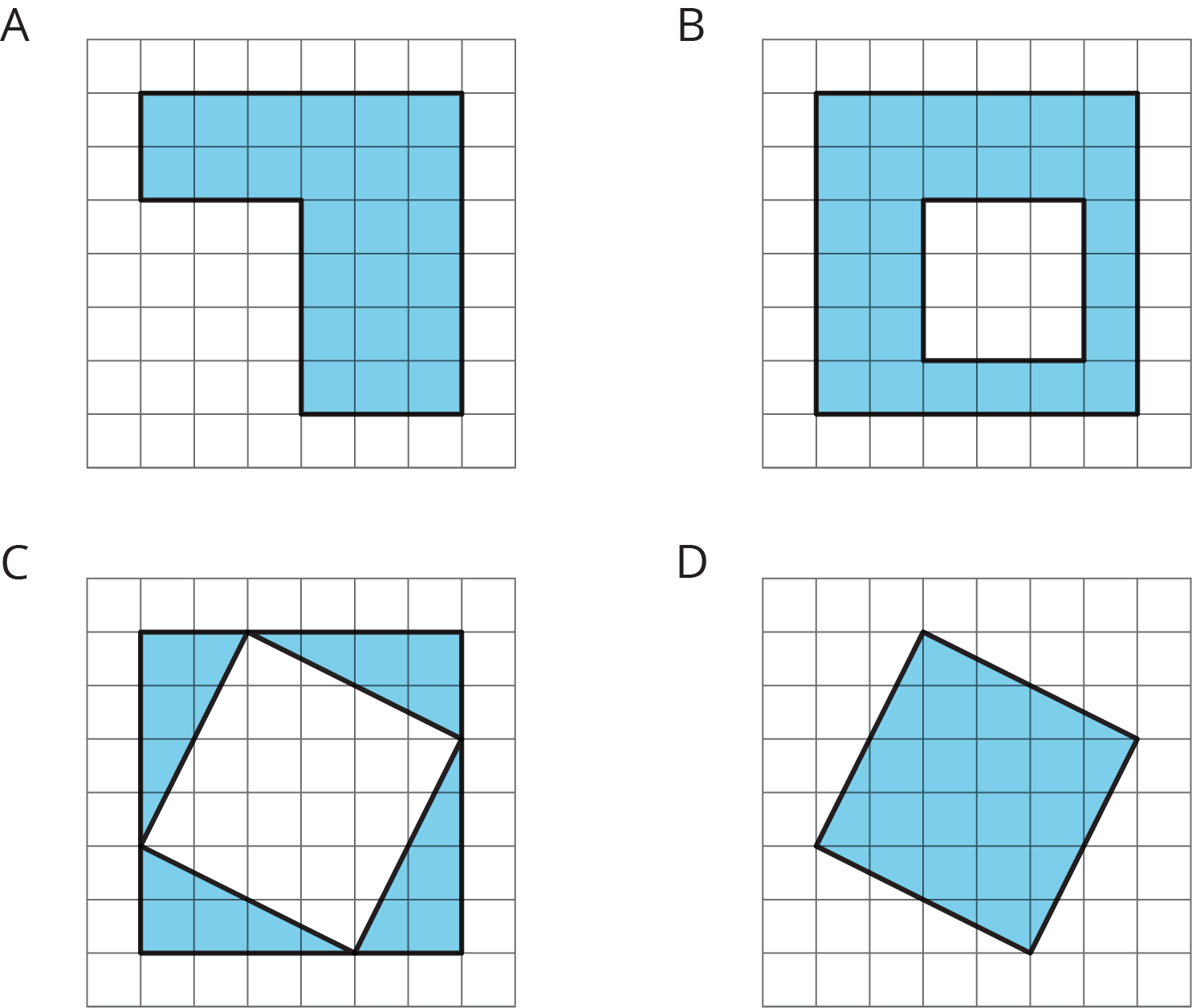
- Figure A can be easily decomposed into rectangles.
- Figure B can be decomposed into rectangles. Or, more efficiently, it can be seen as a square with a missing piece, and the area of the inner unshaded square can be subtracted from the area of the larger square.
- Figure C can also be seen as having a missing piece, but subtracting the area of the unshaded shape does not work because the side lengths of the inner square are unknown. Instead, the shaded triangles can be decomposed and rearranged into rectangles.
- Figure D can be decomposed and rearranged into rectangles. It can also be viewed as the inner square of Figure C.
As students work, identify students who use these strategies and can illustrate or explain them clearly. Ask them to share later. Look for at least two strategies being used for each figure (one strategy as shown in the Student Response and at least one other).
Launch
Tell students that they will find the areas of various figures on a grid. To encourage students to use a more grade-appropriate strategy for finding areas, show them a strategy from earlier grades. As a class, find the area of Figure A by counting the squares one by one aloud. Confirm that there are 24 square units, and then ask students to think about other ways to find the area of Figure A and other figures besides counting each square.
Arrange students in groups of 2. Ask one partner to start with Figures A and C, and the other with B and D. Give students 4–5 minutes of quiet think time, and provide access to their geometry toolkits. Then, give them a few minutes to share their responses with their partner. Emphasize that as one partner explains, the other should listen carefully and see if they agree or disagree with the answer and explanations.
Student Facing
Each grid square is 1 square unit. Find the area, in square units, of each shaded region without counting every square. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Rearrange the triangles from Figure C so they fit inside Figure D. Draw and color a diagram of your work.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may count both complete and partial grid squares instead of looking for ways to decompose and rearrange larger shapes. Ask them if they can find a way to to find the area by decomposing and rearranging larger pieces. The discussion at the end, during which everyone sees a variety of strategies, is especially important for these students.
Activity Synthesis
Discussion should center around how different strategies—decomposing, rearranging, subtracting, and enclosing—are used to find area. For each figure, select two students with different strategies to share their work, if possible. Sequence students’ presentations so that, for each figure, a subtracting strategy comes last, as that is typically the most challenging.
Before sharing begins, explain to students that they should notice similarities and differences in the strategies shared and be ready to explain them. As students share their strategies, consider recording the moves on each figure for all to see. After each person shares, name the strategy, and poll the class to see if anyone else reasoned the same way. If one of these strategies does not appear in students’ work, illustrate it for the class.
- Decomposing (A and B)
- Decomposing and rearranging (C and D)
- Subtracting (B)
- Enclosing, then subtracting (D)
If time permits, give partners a minute to talk to their partner about the similarities and differences they saw in the strategies used to find the areas of the four figures. Consider displaying sentence starters such as:
- The strategies used to find the areas of figures ____ and ____ are alike in that. . .
- The strategies used to find the areas of figures ____ and ____ are different in that. . .
Supports accessibility for: Visual-spatial processing; Conceptual processing
Speaking: Math Language Routine 3 Clarify, Critique, Correct. This is the first time Math Language Routine 3 is suggested as a support in this course. In this routine, students are given an incorrect or incomplete piece of mathematical work. This may be in the form of a written statement, drawing, problem-solving steps, or another mathematical representation. Pairs of students analyze, reflect on, and improve the written work by correcting errors and clarifying meaning. Typical prompts are “Is anything unclear?” or “Are there any reasoning errors?” The purpose of this routine is to engage students in analyzing mathematical thinking that is not their own, and to solidify their knowledge through communicating about conceptual errors and ambiguities in language.
Design Principle(s): Maximize meta-awareness
How It Happens:
- In the class discussion for Figure C of this activity, provide the following “draft” explanation:
“I cut a square in the middle, then I saw that it was a bunch of triangles, so then I figured those out to get my answer.”
Prompt students to identify the ambiguity of this response. Ask students, “What do you think this person is trying to say? What is unclear? Did the author use any of the strategies we’ve been using to find area?”
- Give students 1 minute of individual time to respond to the questions in writing, and then 3 minutes to discuss with a partner.
As pairs discuss, provide these sentence frames for scaffolding: “I think the author is trying to use the strategy _ because.…”, “I think what the author meant by ‘figured it out’ was….”, and “The part that is most unclear to me is … because.…”. Encourage the listener to press for detail by asking follow-up questions to clarify the intended meaning of the statement. Allow each partner to take a turn as the speaker and listener.
- Invite students to improve the “draft” response using the target vocabulary and structures.
The targeted vocabulary includes the names of the strategies (decomposing, rearranging, subtracting, enclosing, or any combination of them), and other terms from this lesson such as “alike,” “different,” “area,” and “polygon.”
The targeted structures of the response should include an explanation of each step, order/time transition words (first, next, then, etc.), and/or reasons for decisions made during steps.
Here is one example of an improved response:
“First, I cut out the square in the middle of the shaded regions. Next, I noticed that all the shaded regions were a bunch of right triangles. Then, I rearranged the triangles into rectangles. Lastly, I figured out the area of each rectangle and added them together to get my answer.”
- Ask each pair of students to contribute their improved response to a poster, the whiteboard, or digital projection. Call on 2–3 pairs of students to present their response to the whole class, and invite the class to make comparisons among the responses shared and their own responses.
Listen for responses that include the strategy of decomposing and then rearranging the triangles. Emphasize that this is one way of figuring out the area of the shaded region.
- Share one more improved response, discuss to reach a general understanding, and then move on to Figure D.
3.3: Off the Grid (15 minutes)
Activity
In this activity, students apply the strategies they learned to find the areas of figures that are not on a grid.
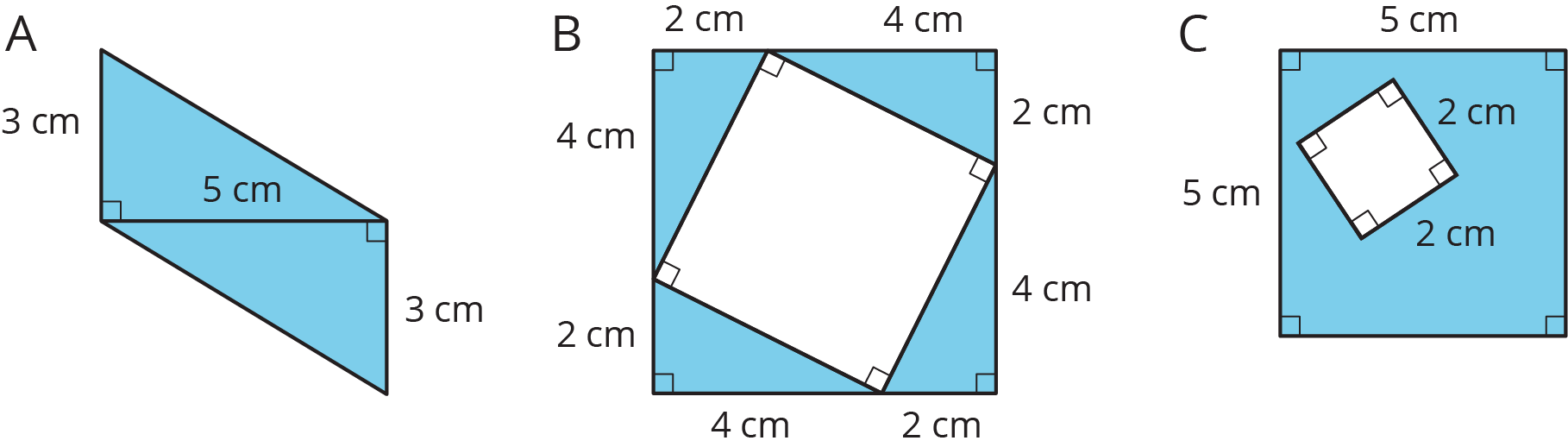
- Figure A can easily be decomposed and rearranged.
- Figure B can be decomposed and rearranged into rectangles as for Figure C of the previous task. Students cannot use the strategy of subtracting the area of the inner square from that of the outer square because the side lengths of the inner square are unknown.
- For Figure C, students must subtract the area of the inner square from that of the outer square because there is not enough information to decompose and rearrange the shaded regions into rectangles.
As students discuss their approaches in groups, support them in naming the strategies and by asking clarifying questions. Notice any groups that may be stuck in a disagreement on the area of a particular figure. Identify students who observed that the same area-reasoning strategies can be applied both on and off the grid.
Students may not remember from earlier grades that if the measurements of side lengths of a rectangle are given in a particular unit, then the area is given in square units. Look for students who have trouble giving the appropriate area units (square centimeters) for these figures.
Launch
Tell students that they will now find areas of figures that are not on a grid. Give students access to their geometry toolkits. Allow for 6–7 minutes of quiet time to find all three areas.
Then, arrange students into groups of 4, and ask each group to discuss their answers and strategies, using these guiding questions:
- What units did you use for each area?
-
Compare your answers and strategies for finding the area of each figure.
- How are your strategies the same? How are they different?
- Which strategies are similar to the ones you used in the previous activity?
Supports accessibility for: Organization; Attention
Student Facing
Find the area of the shaded region(s) of each figure. Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
In Figure B, students may estimate the side lengths of the inner square so that its area could be subtracted from that of the outer square. They may struggle to see how the triangles could be rearranged. Suggest that they use tracing paper to help them in their thinking.
In Figures B and C, students may confuse finding area with finding perimeter. Remind them that area refers to the number of square units it takes to cover a region without gaps or overlaps.
Students might not be familiar with the symbols that indicate right angles and might think these symbols indicate square units. Remind them that those symbols indicate 90 degree angles.
Activity Synthesis
Reconvene briefly as a class to discuss the question, “Which strategies are similar to the ones you used in the previous activity?”
Select 1–2 previously identified students to share (those who noticed that they decomposed, rearranged, enclosed, and subtracted in both activities). Emphasize that the same strategies for finding area can be used whether we use the measurements indicated by a grid, or whether the measurements are given directly (without a grid).
Speaking: Math Language Routine 7 Compare and Connect. This is the first time Math Language Routine 7 is suggested as a support in this course. In this routine, students are given a problem that can be approached using multiple strategies or representations, and are asked to prepare a visual display of their method. Students then engage in investigating the strategies (by means of a teacher-led gallery walk, partner exchange, group presentation, etc.), compare approaches, and identify correspondences between different representations. A typical discussion prompt is, “What is the same and what is different?” regarding their own strategy and that of the others. The purpose of this routine is to allow students to make sense of mathematical strategies by identifying, comparing, contrasting, and connecting other approaches to their own, and to develop students’ awareness of the language used through constructive conversations.
Design Principle(s): Maximize meta-awareness
How It Happens:
- Identify which Figure (A, B, or C) generated the most variety among students’ strategies. Invite students to create a visual display showing how they made sense of this figure. Students should include these features on their display:
Students should include these features on their display:- the drawing of the figure
- appropriate units
- a representation of how the area was calculated
- the name of the strategy used to find the area (decomposing, rearranging, subtracting, enclosing, or any combination of them)
- Arrange students in groups of 4, and invite them to investigate each other’s work. Allow 1 minute for each display and signal when it is time to switch. Next, give each student the opportunity to add detail to their own display for 1-2 minutes.
- Circulate around the room and invite 2–3 students to present their display to the whole class. Be sure to select a variety of strategies.
- After the pre-selected students have finished finished presenting their displays, lead a discussion comparing, contrasting, and connecting the different approaches.
Consider using these prompts to amplify student language while comparing and contrasting the different approaches:- “Why did different approaches for Figure _ lead to the same outcome?”
- “What worked well in this approach for Figure _? What did not work well?”
- “What would make this strategy for Figure _ more complete or easy to understand?”
- “Can you find any connections between the representations?”
- “Where are units used in each strategy?”
- “Is it possible to use the strategy of decomposing for this figure?”
- “What mathematical features do you see present in all of the representations?”
-
Close the discussion by inviting 3 students to revoice the strategies used in the presentations, and then transition back to the Lesson Synthesis and Cool-Down.
Lesson Synthesis
Lesson Synthesis
This lesson was all about identifying strategies for finding area and applying them to various figures. We reasoned about the area of a figure on and off a grid by:
- decomposing it into familiar shapes;
- decomposing it and rearranging the pieces into familiar shapes; or
- considering it as a shape with missing pieces, then subtracting the areas of the missing pieces from the area of the shape.
Ask students to go back through the activities and find problems in which these strategies were used—one strategy at a time. Tell students we will have lots of opportunity to use these strategies in upcoming lessons.
3.4: Cool-down - Maritime Flag (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
There are different strategies we can use to find the area of a region. We can:
- Decompose it into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.
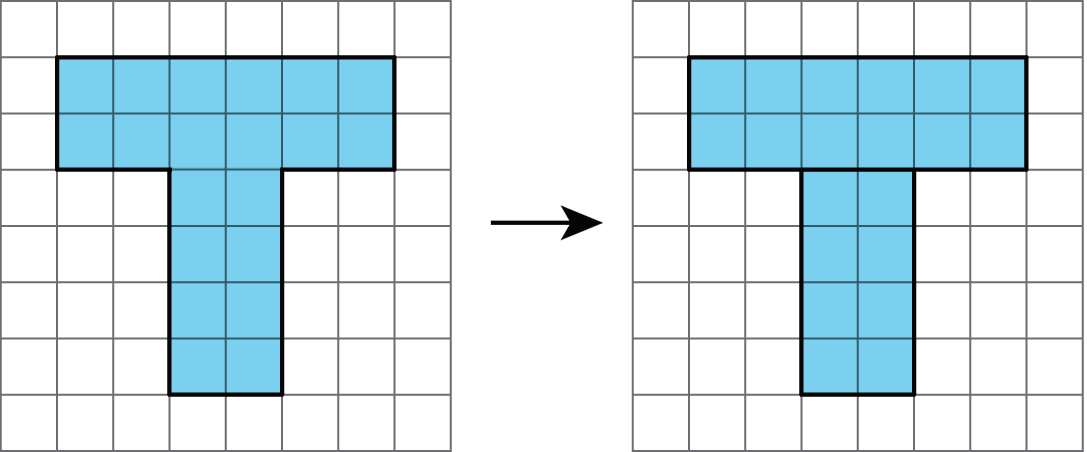
- Decompose it and rearrange the pieces into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.
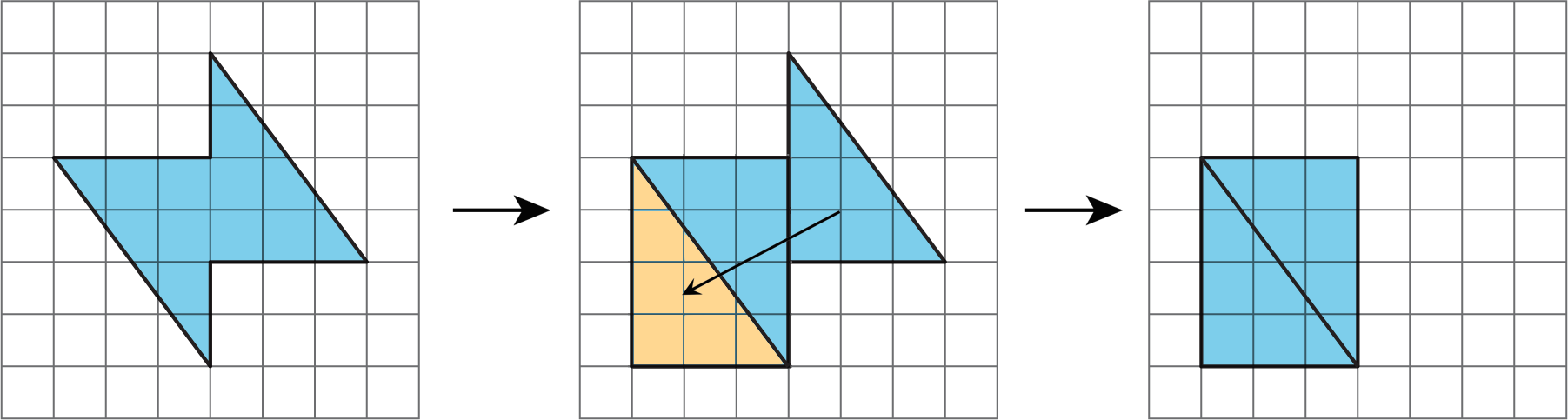
- Consider it as a shape with a missing piece; calculate the area of the shape and the missing piece, and then subtract the area of the piece from the area of the shape.

The area of a figure is always measured in square units. When both side lengths of a rectangle are given in centimeters, then the area is given in square centimeters. For example, the area of this rectangle is 32 square centimeters.
