Lesson 1
Tiling the Plane
1.1: Which One Doesn’t Belong: Tilings (10 minutes)
Warm-up
This warm-up prompts students to compare four geometric patterns, explain their reasoning, and hold mathematical conversations. It allows you to hear how students use terminology in describing geometric characteristics.
Observing patterns gives every student an entry point. Each figure has at least one reason it does not belong. The patterns also urge students to think about shapes that cover the plane without gaps and overlaps, which supports future conversations about the meaning of area.
Before students begin, consider establishing a small, discreet hand signal that students can display to indicate they have an answer they can support with reasoning. This signal could be a thumbs-up, a certain number of fingers that tells the number of responses they have, or another subtle signal. This is a quick way to see if students have had enough time to think about the problem. It also keeps students from being distracted or rushed by hands being raised around the class.
Anticipate students to describe the patterns in terms of:
- Colors (blue, green, yellow, white, or no color)
- Size of shapes or other measurements
- Geometric shapes (polygons, squares, pentagons, hexagons, etc.)
- Relationships of shapes (whether each side of the polygons meets the side of another polygon, what polygon is attached to each side, whether there is a gap between polygons, etc.)
Launch
Arrange students in groups of 2–4. Display the four patterns for all to see. Give students 1 minute of quiet think time and ask them to indicate when they have noticed one pattern that does not belong and can explain why. Encourage them to think of more than one possibility. When the minute is up, give students 2 minutes to share their response with their group, and then together find at least one reason, if possible, that each pattern doesn't belong.
Student Facing
Which pattern doesn’t belong?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students shared their observations in groups, invite each group to share one reason why a particular figure might not belong. Record and display the responses for all to see. After each response, poll the rest of the class to see if others made the same observation.
Since there is no single correct answer to the question of which pattern does not belong, attend to students’ explanations, and make sure the reasons given are correct. Prompt students to explain the meaning of any terminology they use (names of polygons or angles, parts of polygons, area, etc.) and to substantiate their claims. For example, a student may claim that Pattern D does not belong because its polygons all have the same side length. Ask how they know that is the case, and whether that is true for the white (or non-filled) polygon.
Explain to students that covering a two-dimensional region with copies of the same shape or shapes such that there are no gaps or overlaps is called "tiling" the plane. Patterns A, B, and C are examples of tiling. Tell students that we explore more tilings in upcoming activities.
1.2: More Red, Green, or Blue? (25 minutes)
Activity
This activity asks students to compare the amounts of the plane covered by two tiling patterns, with the aim of supporting two big ideas of the unit:
- If two figures can be placed one on top of the other so that they match up exactly, then they have the same area.
- A region can be decomposed and rearranged without changing its area.
Students are likely to notice that in each pattern:
- The same three polygons (triangles, rhombuses, and trapezoids) are used as tiles.
- The entire tiling pattern is composed of these hexagons.
- The shapes are arranged without gaps and overlaps, but their arrangements are different.
- A certain set of smaller tiles form a larger hexagon. Each hexagon has 3 trapezoids, 4 rhombuses, and 7 triangles.
Expect some students to begin their comparison by counting each shape, either within a hexagon or the entire pattern. To effectively compare how much of the plane is covered by each shape, however, they need to be aware of the relationships between the shapes. For example, two green triangles can be placed on top of a blue rhombus so that they match up exactly, which tells us that two green triangles cover the same amount of the plane as one blue rhombus. Monitor for such an awareness. (It is not necessary for students to use the word “area” in their explanations. At this point, phrases such as “they match up” or “two triangles make one rhombus” suffice.)
If students are not sure how to approach the questions, encourage them to think about whether any tools in their geometry toolkits could help. (For example, they could use tracing paper to trace entire patterns or certain shapes to make comparison, or use a straightedge to extend lines within the pattern. Some students may be inclined to cut out and compare the shapes.) Pattern tiles, if available, can be offered as well.
During the partner discussion, monitor for groups who discuss the following ideas so that they can share later, in this sequence:
- Relationships between two shapes: E.g., 2 triangles make a rhombus, and 3 triangles make a trapezoid.
- Relative overall quantities: E.g., there are 56 green triangles, 32 blue rhombuses (which have the same area as 64 triangles), and 24 red trapezoids (which have the same area as 72 triangles), so there is more red.
- Relative quantities in a hexagon: E.g., in each hexagon there are 7 green triangles, 4 rhombuses (which have the same area as 8 triangles), and 3 trapezoids (which have the same area as 9 triangles).
Classrooms using the digital activity have the option for students to use an applet that allows for the pattern to be isolated and also framed. This might assist students in focusing on how many of each shape comprise the pattern.
Launch
Arrange students in groups of 2. Ask one partner to analyze Pattern A and the other to analyze Pattern B. Tell students that their job is to compare the amount of the plane covered by each shape in the pattern.
Before students begin, introduce students to the geometry toolkits, and explain that they can use the toolkits for help, if needed. Give students 7–8 minutes of quiet think time. Then, ask students to share their responses with their partners and follow with a whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Conversing, Speaking, Listening: Math Language Routine 2 Collect and Display.
This is the first time Math Language Routine 2 is suggested as a support in this course. In this routine, the teacher circulates and listens to students talk while writing down the words, phrases, or drawings students produce. The language collected is displayed visually for the whole class to use throughout the lesson and unit. Generally, the display contains different examples of students using features of the disciplinary language functions, such as interpreting, justifying, or comparing. The purpose of this routine is to capture a variety of students’ words and phrases in a display that students can refer to, build on, or make connections with during future discussions, and to increase students’ awareness of language used in mathematics conversations.
Design Principle(s): Support sense-making
How It Happens:
- After assigning students to work on Pattern A or B, circulate around the room and collect examples of language students are using to compare areas of polygons. Focus on capturing a variety of language describing the relationship between the size of two shapes, comparing overall quantities of shapes to equivalent areas of other shapes, and comparing relevant quantities in a hexagon. Aim to capture a range of student language that includes formal, precise, complete ideas and informal, ambiguous, and partial ideas. Plan to publicly update and revise this display throughout the lesson and unit.
If pairs are stuck, consider using these questions to elicit conversation: “How many green triangles, blue rhombuses, and red trapezoids are in each pattern?”, “Three triangles is equivalent to how many trapezoids?”, and “Which shapes make up a hexagon?”
If using the applet, have pairs use the applet together. Check that students focus on how many of each shape comprise the pattern by hiding, moving, and turning the shapes.
- Create a display that includes visual representations of the words and phrases collected. Group language about Pattern A on one side of the display and language about Pattern B on the other side.
- Close this conversation by posting the display in the front of the classroom for students to reference for the remainder of the lesson, and then have students move on to discussing other aspects of the activity. Continue to publicly update and revise the display throughout the lesson and unit.
Student Facing
Your teacher will assign you to look at Pattern A or Pattern B.
In your pattern, which shapes cover more of the plane: blue rhombuses, red trapezoids, or green triangles? Explain how you know.
You may use the sliders and the shapes in this applet to help. Explore what you can see or hide, and what you can move or turn.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Ask one partner to analyze Pattern A and the other to analyze Pattern B. Tell students that their job is to compare the amount of the plane covered by each shape in the pattern.
Before students begin, introduce students to the geometry toolkits, and explain that they can use the toolkits for help, if needed. Give students 7–8 minutes of quiet think time. Then, ask students to share their responses with their partners and follow with a whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Conversing, Speaking, Listening: Math Language Routine 2 Collect and Display.
This is the first time Math Language Routine 2 is suggested as a support in this course. In this routine, the teacher circulates and listens to students talk while writing down the words, phrases, or drawings students produce. The language collected is displayed visually for the whole class to use throughout the lesson and unit. Generally, the display contains different examples of students using features of the disciplinary language functions, such as interpreting, justifying, or comparing. The purpose of this routine is to capture a variety of students’ words and phrases in a display that students can refer to, build on, or make connections with during future discussions, and to increase students’ awareness of language used in mathematics conversations.
Design Principle(s): Support sense-making
How It Happens:
- After assigning students to work on Pattern A or B, circulate around the room and collect examples of language students are using to compare areas of polygons. Focus on capturing a variety of language describing the relationship between the size of two shapes, comparing overall quantities of shapes to equivalent areas of other shapes, and comparing relevant quantities in a hexagon. Aim to capture a range of student language that includes formal, precise, complete ideas and informal, ambiguous, and partial ideas. Plan to publicly update and revise this display throughout the lesson and unit.
If pairs are stuck, consider using these questions to elicit conversation: “How many green triangles, blue rhombuses, and red trapezoids are in each pattern?”, “Three triangles is equivalent to how many trapezoids?”, and “Which shapes make up a hexagon?”
If using the applet, have pairs use the applet together. Check that students focus on how many of each shape comprise the pattern by hiding, moving, and turning the shapes.
- Create a display that includes visual representations of the words and phrases collected. Group language about Pattern A on one side of the display and language about Pattern B on the other side.
- Close this conversation by posting the display in the front of the classroom for students to reference for the remainder of the lesson, and then have students move on to discussing other aspects of the activity. Continue to publicly update and revise the display throughout the lesson and unit.
Student Facing
Your teacher will assign you to look at Pattern A or Pattern B.
In your pattern, which shape covers more of the plane: blue rhombuses, red trapezoids, or green triangles? Explain how you know.
Pattern A
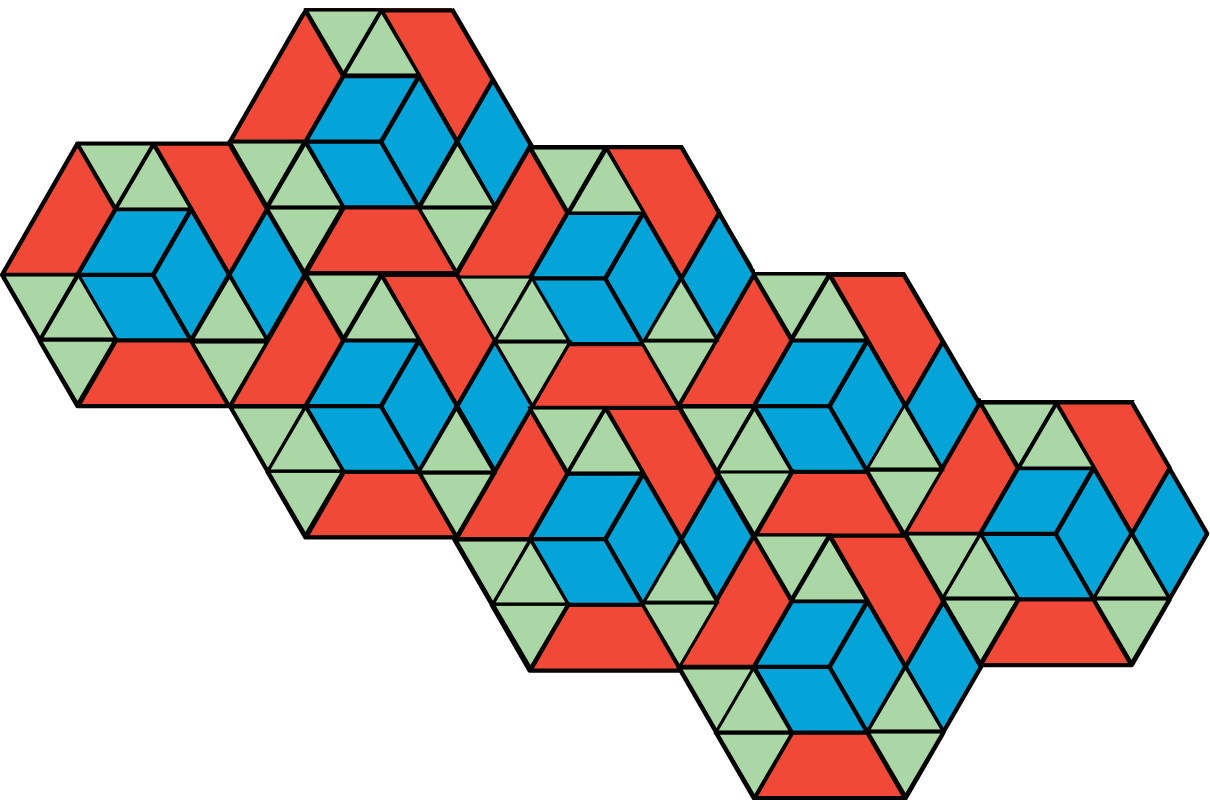
Pattern B
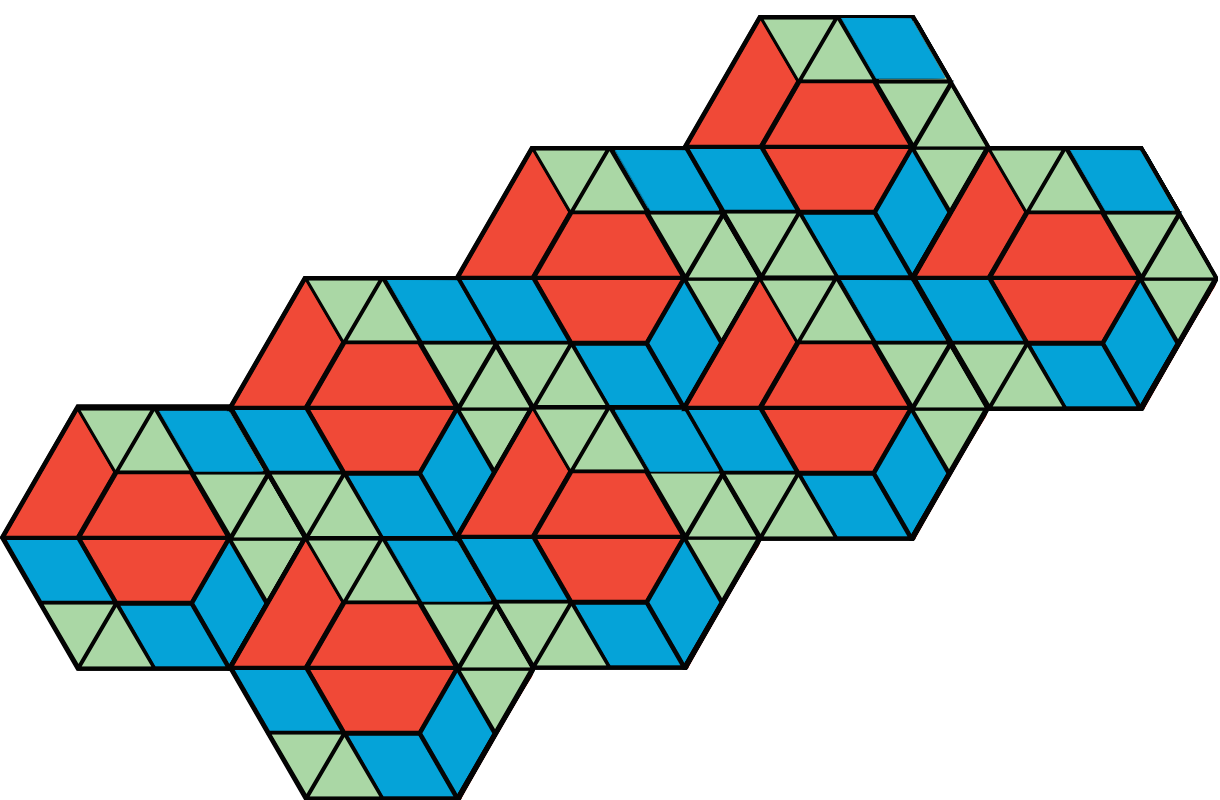
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
On graph paper, create a tiling pattern so that:
- The pattern has at least two different shapes.
- The same amount of the plane is covered by each type of shape.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may say more of the area is covered by the color they see the most in each image, saying, for example, “It just looks like there is more red.” Ask these students if there is a way to prove their observations.
Students may only count the number of green triangles, red trapezoids, and blue rhombuses but not account for the area covered by each shape. If they suggest that the shape with the largest number of pieces covers the most amount of the plane, ask them to test their hypothesis. For example, ask, "Do 2 triangles cover more of the plane than 1 trapezoid?"
Students may not recall the terms trapezoid, rhombus, and triangle. Consider reviewing the terms, although they do not need to know the formal definitions to work on the task.
Activity Synthesis
Select previously identified students or groups to share their answers and explanations. Sequence the explanations in the order listed in the Activity Narrative. To clarify the idea of comparing shapes by placing them on top of one another and seeing if or how they match, consider demonstrating using the digital applet.
Then, make it explicit that when we ask, “Which type of shape covers more of the plane?” we are asking them to compare the areas covered by the different types of shapes. To recast the comparisons of the shapes in terms of area, ask questions such as:
- “How does the area of the trapezoid compare to the area of the triangle?” (The area of the trapezoid is three times the area of the triangle.)
- “How does the area of the rhombus compare to the area of the triangle?” (The area of the rhombus is twice the area of the triangle.)
- “Is it possible to compare the area of the rhombuses in Pattern A and the area of the triangles in Pattern B? How?” (Yes, we can count the number of rhombuses in A and the number of triangles in B. Because 2 triangles have the same area as 1 rhombus, we divide the number of triangles by 2 to compare them.)
Lesson Synthesis
Lesson Synthesis
In this lesson, we have started to reason about what it means for two shapes to have the same area. We started doing mathematics and thinking about tools that can help us. Ask students:
- “What are some of the tools in the geometry toolkit and what are they used for?”
- “Draw two shapes that you know do not have the same area. How can you tell?”
Tell students that we will continue to think about area, to do and talk about mathematics, and to learn to use tools strategically.
1.3: Cool-down - What is Area? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
In this lesson, we learned about tiling the plane, which means covering a two-dimensional region with copies of the same shape or shapes such that there are no gaps or overlaps.
Then, we compared tiling patterns and the shapes in them. In thinking about which patterns and shapes cover more of the plane, we have started to reason about area.
We will continue this work, and to learn how to use mathematical tools strategically to help us do mathematics.