Lesson 4
Parallelograms
4.1: Features of a Parallelogram (10 minutes)
Warm-up
Prior to grade 6, students learned that lines are parallel if they never intersect. In this activity, students look at the defining attributes of parallelograms—a quadrilateral whose opposite sides are parallel. They observe other properties that follow from that definition—that opposite sides of a parallelogram have the same length and opposite angles have the same measure.
Students’ initial investigation of parallelograms should involve lots of examples and non-examples, giving them opportunities to look for and express regularity in repeated reasoning (MP8) and seek and make use of structure (MP7). This activity assumes that students have had some exposure to parallelograms, but is also accessible to students who have not.
Launch
Display the image of figures A–F for all to see. Give students a minute to observe it and to prepare to share at least one thing they notice and one thing they wonder. When the minute is up, invite students to share their responses with the class.
Students may notice that:
- all except one figure (E) are quadrilaterals.
- figures C and E have sides that are all equal in length.
- figures A and B have two pairs of equal sides.
- figures B and C are rectangles.
- none of the sides in D are parallel.
- two of the sides in F are parallel.
They may wonder:
- why a hexagon is in the set.
- if the sides of figure A are all equal.
- if figure C is a parallelogram.
One or more students are likely to mention “parallelogram” in their observations or questions. Tell students that they will look closely at parallelograms in this lesson. Read aloud the opening sentences in the task statement. Clarify that A, B, and C are examples of parallelograms, and that D, E, and F are non-examples (i.e., they are not parallelograms).
Arrange students into groups of 2 and give them geometry toolkits. Give students 3 minutes of quiet think time to complete the task. Afterwards, give them a minute to discuss their answers and observations with their partner.
Student Facing
Figures A, B, and C are parallelograms. Figures D, E, and F are not parallelograms.
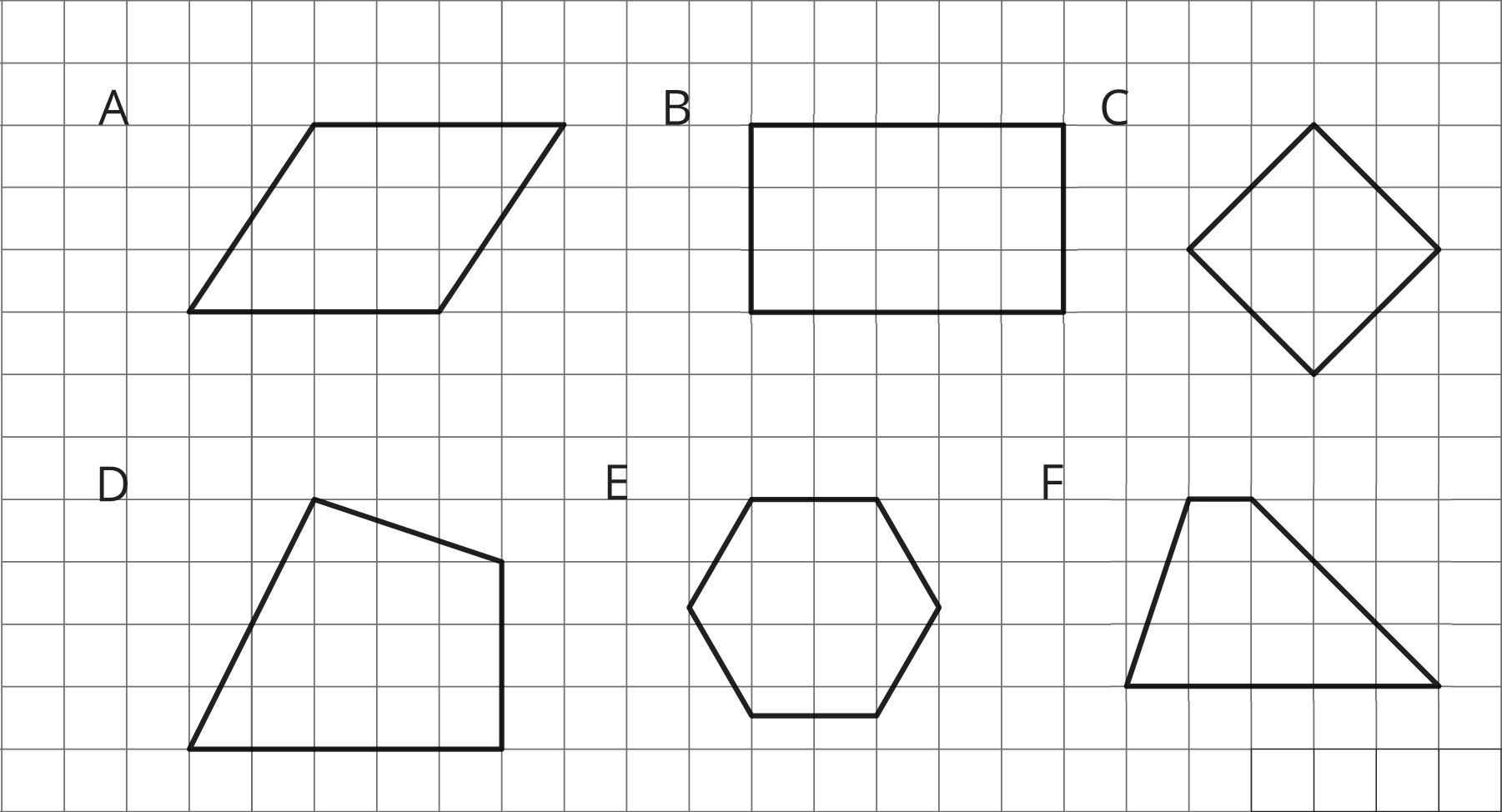
Study the examples and non-examples. What do you notice about:
- the number of sides that a parallelogram has?
- opposite sides of a parallelogram?
- opposite angles of a parallelogram?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may have trouble seeing C as a square because of its orientation. They may also think that squares and rectangles are not parallelograms. Explain that the definition we are using for parallelograms is: a quadrilateral where both pairs of opposite sides are parallel. By that definition, rectangles and squares are special kinds of parallelograms.
If students wonder how they would know if two sides are parallel, explain that a consequence of “never intersecting” is that the length of a perpendicular line segment between them always has the same length. Students can use an index card to check this in figures A and C.
Activity Synthesis
Ask a few students to share their responses to the questions. After each response, ask students to indicate whether they agree. If a student disagrees, discuss the disagreement. Record the agreed-upon responses for all to see and highlight that:
- A parallelogram is a polygon with four sides, and both pairs of opposite sides are parallel.
- Opposite sides have equal length.
- Opposite angles have equal measure.
Tell students that for now we will just take properties about parallelograms as facts, and that later on in their schooling they will learn some ways to prove that they are always true.
If time permits, revisit figures D, E, and F. Ask students to explain why these are non-examples and see if students connect their explanations to the properties of parallelogram.
- “Why is figure D not a parallelogram?”
- “Why is figure E not a parallelogram? What about F?”
4.2: Area of a Parallelogram (15 minutes)
Activity
In this activity, students explore different methods of decomposing a parallelogram and rearranging the pieces to find its area. Presenting the parallelograms on a grid makes it easier for students to see that the area does not change as they decompose and rearrange the pieces.
This investigation lays a foundation for upcoming work with area of triangles and other polygons. Here are the two key approaches for finding the area of parallelograms:
- Decompose the parallelogram, rearrange the parts into a rectangle, and multiply the side lengths of the rectangle to find the area.
- Enclose the parallelogram in a rectangle and subtract the combined area of the extra regions.
As students work and discuss, monitor for these approaches. Identify students whose reasoning can highlight the usefulness of a related rectangle for finding the area of a parallelogram.
Some students may begin by counting squares because it is a strategy used in earlier grades. This strategy is not reinforced here. Instead, encourage students to listen for and try more sophisticated, grade-appropriate methods shared during the class discussion.
In the digital version of the activity, students are given rectangles and right triangles as tools to visualize their reasoning (decomposition, rearrangement, and enclosure).
Launch
Arrange students in groups of 2–4. Ask students to find the area of the parallelogram using recently learned strategies and tools. Prepare extra copies of the task in case students wish to cut the parallelogram out.
Give students 5 minutes of quiet think time and access to their toolkits. Ask them to share their strategies with their group afterwards.
To encourage students to be mindful of their strategies and to plant the seed for the whole-class discussion, display and read aloud the following reflection questions before students begin working.
- Why did you decompose the parallelogram the way you did?
- Why did you rearrange the pieces the way you did?
For digital classrooms, project the applet to introduce it. Ask students to experiment with the given polygons to find the area of the parallelograms. For the second question, students are given the same starting parallelogram as in the first question. They will need to move the vertices to change it into a different parallelogram before finding its area.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
-
Find the area of the parallelogram and explain your reasoning.
-
Change the parallelogram by dragging the green points at its vertices. Find its area and explain your reasoning.
- If you used the polygons on the side, how were they helpful? If you did not, could you use one or more of the polygons to show another way to find the area of the parallelogram?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2–4. Ask students to find the area of the parallelogram using recently learned strategies and tools. Prepare extra copies of the task in case students wish to cut the parallelogram out.
Give students 5 minutes of quiet think time and access to their toolkits. Ask them to share their strategies with their group afterwards.
To encourage students to be mindful of their strategies and to plant the seed for the whole-class discussion, display and read aloud the following reflection questions before students begin working.
- Why did you decompose the parallelogram the way you did?
- Why did you rearrange the pieces the way you did?
For digital classrooms, project the applet to introduce it. Ask students to experiment with the given polygons to find the area of the parallelograms. For the second question, students are given the same starting parallelogram as in the first question. They will need to move the vertices to change it into a different parallelogram before finding its area.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Find the area of each parallelogram. Show your reasoning.
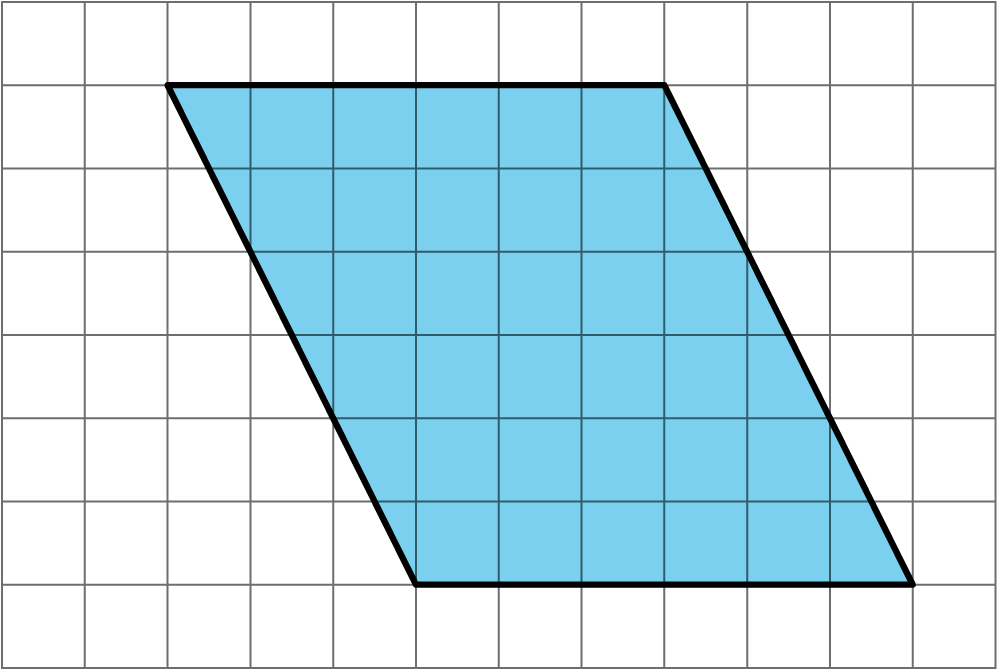
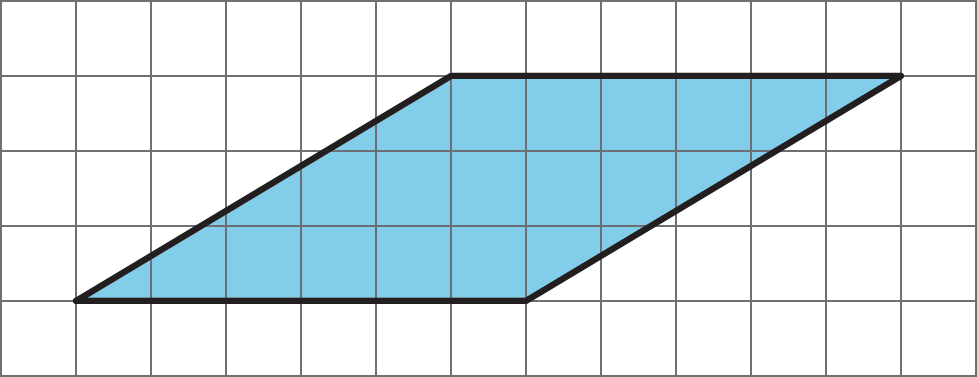
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to share how they found the area of the first parallelogram. Begin with students who decomposed the parallelogram in different ways. Follow with students who enclosed the parallelogram and rearranged the extra right triangles.
As students share, display and list the strategies for all to see. (Restate them in terms of decomposing, rearranging, and enclosing, as needed.) The list will serve as a reference for upcoming work. If one of the key strategies is not mentioned, illustrate it and add it to the list.
Use the reflection questions in the Launch to help highlight the usefulness of rectangles in finding the area of parallelograms. Consider using the applet to illustrate this point, https://ggbm.at/kj5DcRvn.
Supports accessibility for: Visual-spatial processing; Conceptual processing
4.3: Lots of Parallelograms (15 minutes)
Activity
In this activity, students continue to reason about areas of parallelograms, both on and off the grid.
While there is not one correct way to find the area of a parallelogram, each parallelogram here is designed to elicit a particular strategy. parallelograms A and C encourage decomposing and rearranging the parallelograms into a rectangle. Parallelogram B is not as easy to decompose and rearrange (though some students are likely to first try that approach), and may prompt students to enclose the parallelograms and subtract the areas of the extra pieces. The grid and its absence allow students to reason concretely and abstractly, respectively, about the measurements that they need to find the area.
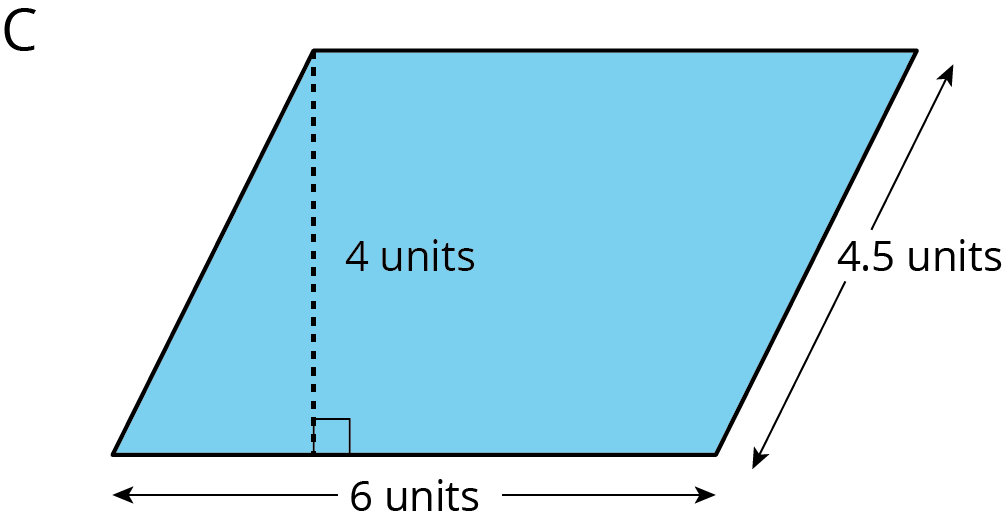
As students work, monitor for uses of the two main strategies—decompose-and-rearrange and enclose-and-subtract. The three measurements in Parallelogram C may give students pause. Notice students who are able to reason about why the side that is 4.5 inches long is not needed for finding the area of the parallelogram.
With repeated reasoning, students may begin to see the segments and measurements that tend to be useful in finding area (MP8). There are no references to bases or heights in this lesson, but highlighting the segments and measurements that helped students reason about area here can help to support students’ future work. In the next lesson, awareness of the measurements that affect the area of a parallelogram will be formalized.
Launch
Keep students in groups of 2–4 and ask them to find the areas of several more parallelograms. Give them 7–8 minutes of quiet think time, followed by a couple of minutes to share their strategies with their groups. Ask students to attempt at least the first two questions individually before discussing with their group. Provide access to their geometry toolkits.
To prepare for the whole-class discussion, consider asking students to think, as they work through the problems, about what measurements of the parallelogram seem to be helpful for finding its area.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
Find the area of each parallelogram. Show your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may think that it is not possible to decompose and rearrange Parallelogram A because it has a pair of vertical sides instead of a pair of horizontal sides. Rotating their paper 90 degrees and back might help them see that they could still use the same reasoning strategy. Or they may find it helpful to first reason about area with the parallelogram rotated 90 degrees and then rotating it back to its original orientation.
Activity Synthesis
For each parallelogram, select 1–2 students with differing strategies to share their work with the class, starting with the less-efficient strategy. If an important strategy is not mentioned, bring it up and illustrate it. Briefly poll the class to see how others approached the problem. After hearing from students on each problem, consider asking questions such as the following. Focus the discussion on parallelograms B and C.
- “Is Parallelogram A different than others you have seen so far? How so?” (Students may answer yes or no, but some may see it as different because it has a pair of vertical sides.) “Can it still be decomposed and rearranged into a shape whose area we know how to calculate?” (Yes.)
- “Which strategy—decomposing and rearranging, or enclosing and subtracting—seems more practical for finding a parallelogram such as B? Why?” (Enclosing and subtracting, because it can be done in fewer steps. Decomposing the figure into small pieces could get confusing and lead to errors.)
- “If you decomposed C into a right triangle and another shape, how do you know that the cut-out piece actually fits on the other side, given that there's no grid to verify?” (The two opposite sides are of a parallelogram are parallel, so the longest (slanted) side of the right triangle that is rearranged would match up perfectly with the segment on the other side. Make available tracing paper or a copy of the drawing for cutting and rearranging physically so students can verify.)
- “Three measurements are shown for Parallelogram C. Which ones did you use? Which ones did you not use? Why and why not?” (The 4 units and 6 units are side lengths of a rectangle that has the same area of the parallelogram. If we decompose the parallelogram with a vertical cut and move the piece on the left to the right to make a rectangle, the 4.5-unit length is no longer relevant.)
- “Why did your strategy make the most sense to you for this parallelogram?”
To help students make connections and generalize their observations, ask questions such as:
- “When you decomposed and rearranged the parallelogram into another shape, did the area change?” (No.)
- “Why use a rectangle?”(We know how to find the area of a rectangle; we can multiply the two side lengths.)
- “For those of you who enclosed the parallelogram with a rectangle, how did the two right triangles help you?” (They can be combined into a rectangle, whose area we can find and subtract from the area of a large rectangle.)
- “Which measurements or lengths were useful for finding the area of the parallelogram?" (One side length of the parallelogram and the length of a perpendicular segment between that side and the opposite side.) Which lengths did you not use?” (The other side length.)
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
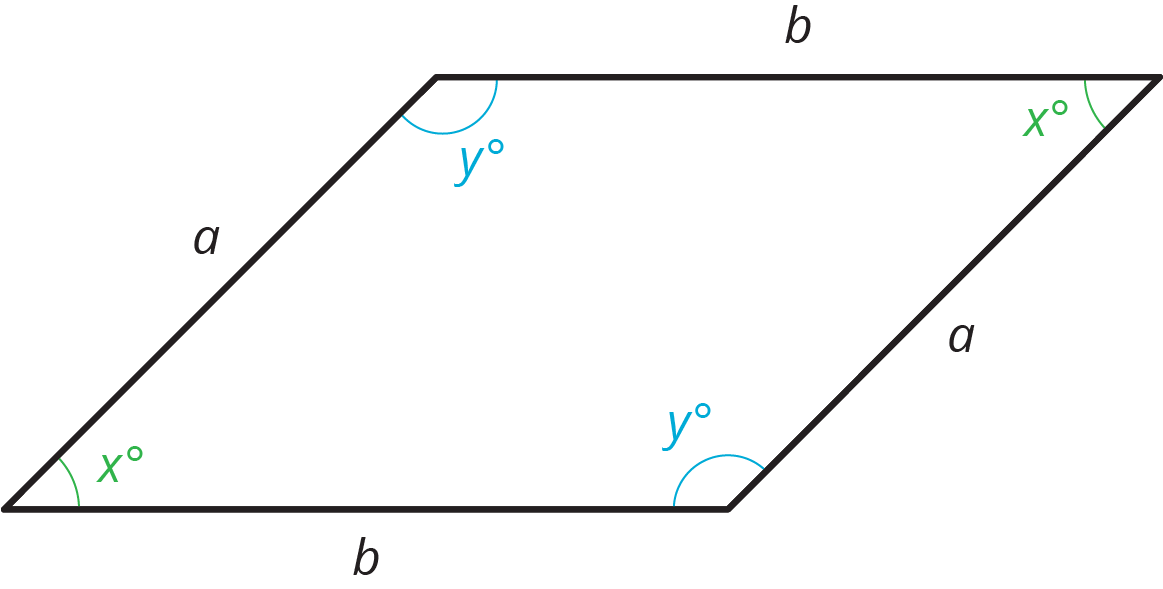
Revisit the definition of a parallelogram with students: A parallelogram has four sides. The opposite sides of a parallelogram are parallel. Remind them that, as a result of the sides being parallel, it is also true that:
- The opposite sides of a parallelogram have equal length.
- The opposite angles of a parallelogram have equal measure.
Tell students that, while we are just taking these properties as facts for now, in later grades they will be able to prove these for themselves.
Briefly revisit the last task, displaying for all to see the multiple area strategies students used. Point out that in some cases, students chose to decompose and rearrange parts, and in others they chose to enclose the parallelogram with a rectangle and subtract the area of the extra pieces from the area of the rectangle. Ask about a couple of the parallelograms: “What was it about that parallelogram that prompted that particular choice?”
4.4: Cool-down - How Would You Find the Area? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A parallelogram is a quadrilateral (it has four sides). The opposite sides of a parallelogram are parallel. It is also true that the opposite sides of a parallelogram have equal length, and the opposite angles of a parallelogram have equal measure.

There are several strategies for finding the area of a parallelogram.
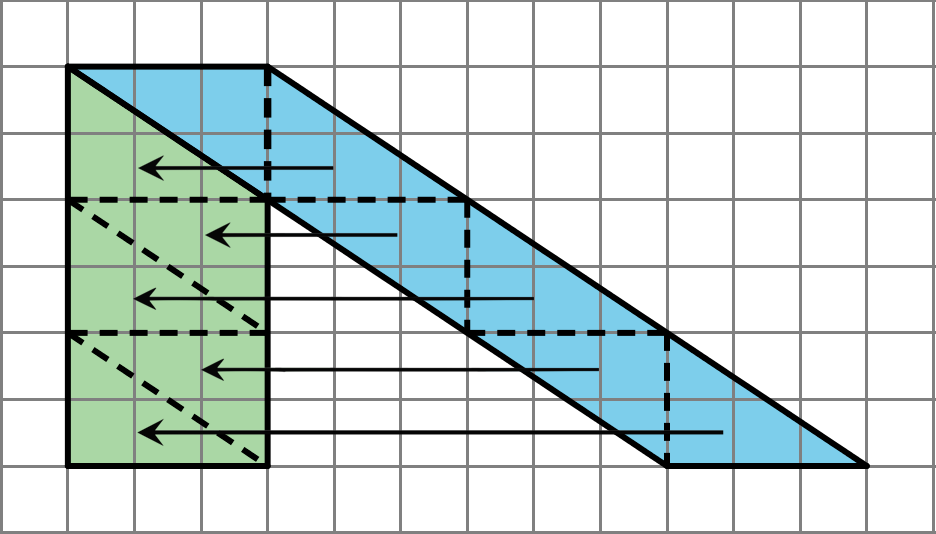
- We can decompose and rearrange a parallelogram to form a rectangle. Here are three ways:

- We can enclose the parallelogram and then subtract the area of the two triangles in the corner.

Both of these ways will work for any parallelogram. However, for some parallelograms the process of decomposing and rearranging requires a lot more steps than if we enclose the parallelogram with a rectangle and subtract the combined area of the two triangles in the corners.