Lesson 17
Squares and Cubes
17.1: Perfect Squares (5 minutes)
Warm-up
This activity introduces the concept of perfect squares. It also includes opportunities to practice using units of measurement, which offers insights on students’ knowledge from preceding lessons.
Provide access to square tiles, if available. Some students may benefit from using physical tiles to reason about perfect squares.
As students work, notice whether they use appropriate units for the second and third questions.
Launch
Tell students, “Some numbers are called perfect squares. For example, 9 is a perfect square. Nine copies of a small square can be arranged into a large square.” Display a square like this for all to see:

Explain that 10, however, is not a perfect square. Display images such as these below, emphasizing that 10 small squares can not be arranged into a large square (the way 9 small squares can).

Tell students that in this warm-up they will find more numbers that are perfect squares. Give students 2 minutes of quiet think time to complete the activity.
Student Facing
- The number 9 is a perfect square. Find four numbers that are perfect squares and two numbers that are not perfect squares.
- A square has side length 7 in. What is its area?
- The area of a square is 64 sq cm. What is its side length?

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students do not recall what the abbreviations km, cm, and sq stand for, provide that information.
Students may divide 64 by 2 for the third question. If students are having trouble with this, ask them to check by working backwards, i.e. by multiplying the side lengths to see if the product yields the given area measure.
Activity Synthesis
Invite students to share the examples and non-examples they found for perfect squares. Solicit some ideas on how they decided if a number is or is not a perfect square.
If a student asks about 0 being a perfect square, wait until the end of the lesson, when the exponent notation is introduced. 0 is a perfect square because \(0^2 = 0\).
Briefly discuss students’ responses to the last two questions, the last one in particular. If not already uncovered in discussion, highlight that because the area of a square is found by multiplying side lengths to each other, finding the side lengths of a square with a known area means figuring out if that area measure is a product of two of the same number.
17.2: Building with 32 Cubes (15 minutes)
Optional activity
This activity gives students a concrete way to review the work on volume from grade 5. It prompts students to recall that the volume of a rectangular prism can be calculated in two different ways: by counting unit cubes that can be packed into the prism, and by multiplying the edge lengths of the prism. Students also become familiar with two perfect cubes, 27 and 64, before the next activity introduces this term.
As students work, monitor the different routes they take to find the volume of the built cube. They may count all of the snap cubes individually, count the number of snap cubes per layer and then multiply that by the number of layers, or simply multiply edge lengths. Select a student who uses each method to share later.
Launch
Arrange students in groups of 2. Give 32 snap cubes to each group. If centimeter cubes are available, have students work in centimeters instead of the generic units listed here. Give students 8–10 minutes to build the largest cube they can with 32 cubes and to answer the questions.
For groups who finish early, consider asking them to combine their cubes and build the largest single cube they can with 64 cubes. Then, ask them to answer the same four questions as shown in the problem statement.
Students in digital classrooms can use the applet to build the cube with 32 cubes. For students who finish early, another applet with 64 cubes can be found in Digital Extension.
Student Facing
Use the 32 snap cubes in the applet’s hidden stack to build the largest single cube you can. Each small cube has side length of 1 unit.
- How many snap cubes did you use?
- What is the side length of the cube you built?
- What is the area of each face of the built cube? Show your reasoning.
- What is the volume of the built cube? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
This applet has a total of 64 snap cubes. Build the largest single cube you can.
- How many snap cubes did you use?
- What is the edge length of the new cube you built?
- What is the area of each face of this built cube? Show your reasoning.
- What is the volume of this built cube? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Give 32 snap cubes to each group. If centimeter cubes are available, have students work in centimeters instead of the generic units listed here. Give students 8–10 minutes to build the largest cube they can with 32 cubes and to answer the questions.
For groups who finish early, consider asking them to combine their cubes and build the largest single cube they can with 64 cubes. Then, ask them to answer the same four questions as shown in the problem statement.
Students in digital classrooms can use the applet to build the cube with 32 cubes. For students who finish early, another applet with 64 cubes can be found in Digital Extension.
Student Facing
Your teacher will give you 32 snap cubes. Use them to build the largest single cube you can. Each small cube has an edge length of 1 unit.
- How many snap cubes did you use?
- What is the edge length of the cube you built?
- What is the area of each face of the built cube? Be prepared to explain your reasoning.
- What is the volume of the built cube? Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may neglect to write units for length or area and may need a reminder to do so.
When determining area, students may multiply a side by two instead of squaring it. When determining volume, they may multiply a side by three instead of cubing it. If this happens, ask them to count individual squares so that they can see that there is an error in their reasoning.
Activity Synthesis
Focus the whole-class discussion on the ways students calculated the volumes of the two cubes they built. Select previously identified students to share their approaches starting from the less efficient (counting individual cubes) to the most efficient (multiplying side lengths).
Highlight how the side length of a cube determines its volume, and specifically that the number 27 is \(3\boldcdot 3\boldcdot 3\). If any group built a cube with 64 snap cubes, point out that the number 64 is \(4\boldcdot 4\boldcdot 4\). These observations prepare students to think about perfect cubes in the next activity and about a general expression for the volume of a cube later in the lesson.
17.3: Perfect Cubes (10 minutes)
Activity
Earlier, students looked at examples and non-examples of perfect squares. In this activity, they think about examples and non-examples of perfect cubes and find the volumes of cubes given their edge lengths. Students see that the edge length of a cube determines its volume, notice the numerical expressions that can be written when calculating volumes, and write a general expression for finding the volume of a cube (MP8).
Some students may feel uncomfortable writing the answer to the last question symbolically because it involves a variable and may prefer writing a verbal explanation. This is fine; the exponential notation that follows will help greatly.
Launch
Tell students, “Some numbers are called perfect cubes. For example, 27 is a perfect cube.” Display a cube like this for all to see:
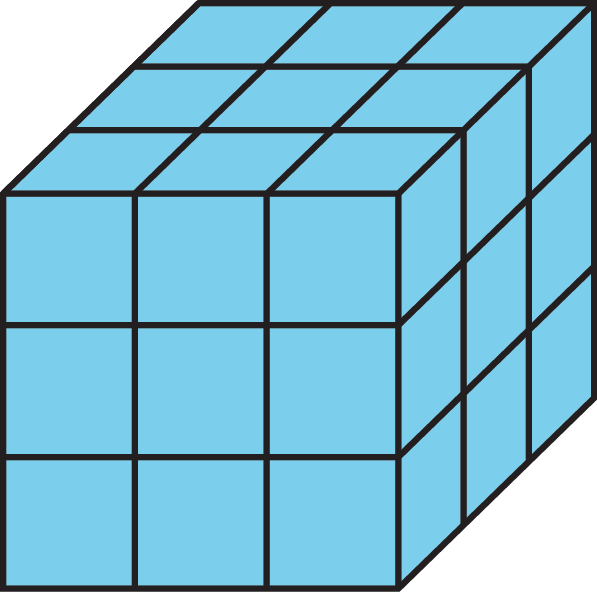
Arrange students in groups of 2. Give students a few minutes of quiet think time, and another minute to discuss their responses with their partner.
Supports accessibility for: Conceptual processing
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
- The number 27 is a perfect cube. Find four other numbers that are perfect cubes and two numbers that are not perfect cubes.
- A cube has side length 4 cm. What is its volume?
- A cube has side length 10 inches. What is its volume?
- A cube has side length \(s\) units. What is its volume?

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Watch for students using square units instead of cubic units. Remind them that volume is a measure of the space inside the cube and is measured in cubic units.
Students may multiply by 3 when finding the volume of a cube instead of multiplying three edge lengths (which happen to be the same number). Likewise, they may think a perfect cube is a number times 3. Suggest that they sketch or build a cube with that edge length and count the number of unit cubes. Or ask them to think about how to find the volume of a prism when the edge lengths are different (e.g., a prism that is 1 unit by 2 units by 3 units).
Activity Synthesis
After partner discussions, invite students to share how they thought about the first question and decided if a number is or is not a perfect cube. Highlight the idea that multiplying three edge lengths allows us to determine volume efficiently, and that determining if a number is a perfect cube involves thinking about whether it is a product of three of the same number.
If a student asks about 0 being a perfect cube, wait until the end of the lesson, when exponent notation is introduced. 0 is a perfect cube because \(0^3 = 0\).
Make sure students see the answers to the last three questions written as expressions: \(\displaystyle 4 \boldcdot 4 \boldcdot 4\) \(\displaystyle 10 \boldcdot 10 \boldcdot 10\) \(\displaystyle s \boldcdot s \boldcdot s\)
17.4: Introducing Exponents (15 minutes)
Activity
This activity introduces students to the exponents of 2 and 3 and the language we use to talk about them. Students use and interpret this notation in the context of geometric squares and their areas, and geometric cubes and their volumes. Students are likely to have seen exponent notation for \(10^3\) in their work on place values in grade 5. That experience would be helpful but is not necessary.
Note that the term “exponent” is deliberately not defined more generally at this time. Students will work with exponents in more depth in a later unit.
As students work, observe how they approach the last two questions. Identify a couple of students who approach the fourth question differently so they can share later. Also notice whether students include appropriate units, written using exponents, in their answers.
Launch
Ask students if they have seen an expression such as \(10^3\) before. Tell students that in this expression, the 3 is called an exponent. Explain the use of exponents of 2 and 3:
- “When we multiply two of the same number together, such as \(5 \boldcdot 5\), we say we are squaring the number. We can write the expression as: \(\displaystyle 5^2\) Because \(5\boldcdot 5\) is 25, we can write \(5^2 = 25\), and we say, ‘5 squared is 25.’ We can also say that 25 is a perfect square. The raised 2 in \(5^2\) is called an exponent.”
- “When we multiply three of the same number together like \(4 \boldcdot 4 \boldcdot 4\), we say we are cubing the number. We can write it like this: \(\displaystyle 4^3\) Because \(4 \boldcdot 4 \boldcdot 4\) is 64, we can write \(4^3 = 64\), and we say, ‘4 cubed is 64.’ We also say that 64 is a perfect cube. The raised 3 in \(4^3\) is called an exponent.”
Explain that we can also use exponents as a shorthand for the units used for area and volume:
- A square with side length 5 inches has area of 25 square inches, which we can write as 25 in2.
- A cube with edge length 4 centimeters has a volume of 64 cubic centimeters, which we can write as 64 cm3.
Ask students to read a few areas and volumes in different units (e.g. 100 ft2 is read “100 square feet” and 125 yd3 is read “125 cubic yards”).
Keep students in groups of 2. Give students 3–4 minutes of quiet time to complete the activity and a minute to discuss their response with their partner. Ask partners to note any disagreements so they can be discussed.
Student Facing
Make sure to include correct units of measure as part of each answer.
- A square has side length 10 cm. Use an exponent to express its area.
- The area of a square is \(7^2\) sq in. What is its side length?
- The area of a square is 81 m2. Use an exponent to express this area.
- A cube has edge length 5 in. Use an exponent to express its volume.
- The volume of a cube is \(6^3\) cm3. What is its edge length?
- A cube has edge length \(s\) units. Use an exponent to write an expression for its volume.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The number 15,625 is both a perfect square and a perfect cube. It is a perfect square because it equals \(125^2\). It is also a perfect cube because it equals \(25^3\). Find another number that is both a perfect square and a perfect cube. How many of these can you find?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Upon seeing \(6^3\) in the fifth question, some students may neglect to interpret the question, automatically calculate \(6\boldcdot 6\boldcdot 6\), and conclude that the edge length is 216 cm. Ask them to check their answer by finding the volume of a cube with edge length 216 cm.
Activity Synthesis
Ask partners to share disagreements in their responses, if any. Then, focus the whole-class discussion on the last two questions. Select a couple of previously identified students to share their interpretations of the fourth question.
Highlight that a cube with a volume of \(6^3\) cubic units has an edge length of 6 units, because we know there are \(6 \boldcdot 6 \boldcdot 6\) unit cubes in a cube with that edge length.
In other words, we can express the volume of a cube using a number (216), a product of three numbers (\(6 \boldcdot 6 \boldcdot 6\)), or an expression with exponent (\(6^3\)). This idea can be extended to all cubes. The volume of a cube with edge length \(s\) is: \(\displaystyle s \boldcdot s \boldcdot s\) \(\displaystyle s^3\) Students will have more opportunities to generalize the expressions for the volume of a cube in the next lesson.
Supports accessibility for: Conceptual processing; Language; Memory
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Review the language and notation for squaring and cubing a number. Remind students we use this notation for square and cubic units, too.
-
When we multiply two of the same number together like \(10\boldcdot 10\) we say we are squaring the number. We write, for example, \(10^2 = 100\) and say, “Ten squared is one hundred.”
-
When we multiply three of the same number together like \(10 \boldcdot 10 \boldcdot 10\), we say we are cubing the number. We write, for example, \(10^3 = 1,\!000\) and say, “Ten cubed is one thousand.”
-
Exponents are used to write square and cubic units. The area of a square with side length 7 km is \(7^2\) km2. The volume of a cube with side length 2 millimeters is \(2^3\) mm3.
17.5: Cool-down - Exponent Expressions (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When we multiply two of the same numbers together, such as \(5\boldcdot 5\), we say we are squaring the number. We can write it like this: \(\displaystyle 5^2\)
Because \(5\boldcdot 5 = 25\), we write \(5^2 = 25\) and we say, “5 squared is 25.”
When we multiply three of the same numbers together, such as \(4\boldcdot 4 \boldcdot 4\), we say we are cubing the number. We can write it like this: \(\displaystyle 4^3\)
Because \(4\boldcdot 4\boldcdot 4 = 64\), we write \(4^3 = 64\) and we say, “4 cubed is 64.”
We also use this notation for square and cubic units.
- A square with side length 5 inches has area 25 in2.
- A cube with edge length 4 cm has volume 64 cm3.
To read 25 in2, we say “25 square inches,” just like before.
The area of a square with side length 7 kilometers is \(7^2\) km2. The volume of a cube with edge length 2 millimeters is \(2^3\) mm3.
In general, the area of a square with side length \(s\) is \(s^2\), and the volume of a cube with edge length \(s\) is \(s^3\).