Lesson 14
Nets and Surface Area
14.1: Matching Nets (10 minutes)
Warm-up
This warm-up prompts students to match nets to polyhedra. It invites them to think about the polygons that make up a polyhedron and to mentally manipulate nets, which helps develop their visualization skills.
Launch
Give students 3 minutes of quiet think time to match nets to polyhedra and then another 2 minutes to discuss their response and reasoning with a partner. Encourage students to use the terminology they learned in prior lessons.
To support students who need more time or help in visualization, prepare physical models of the polyhedra and copies of the nets from the blackline master. Pre-cut the nets or have scissors available so that students can assemble the nets and test their ideas.
Student Facing
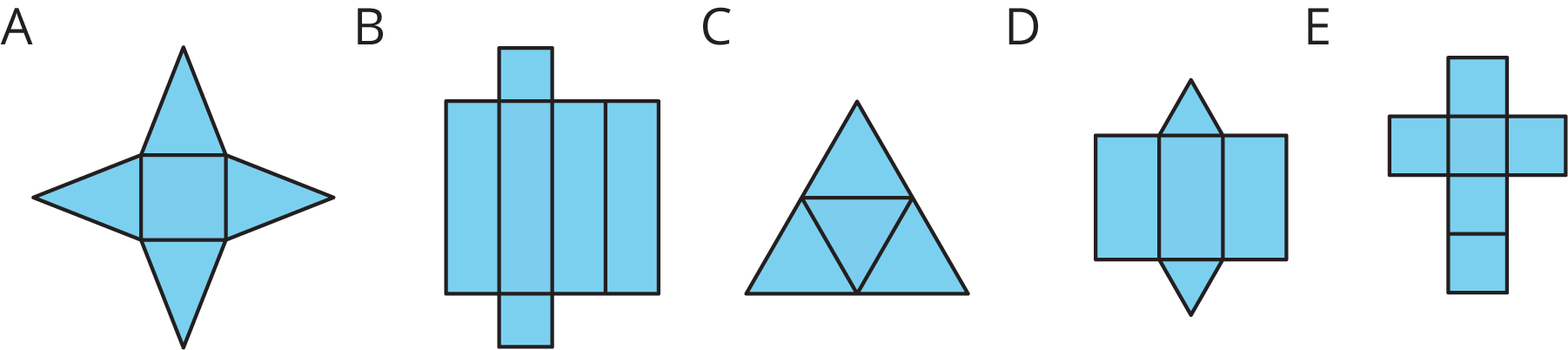
Each of the nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students have trouble distinguishing between figures A, C, and D, remind them that prisms and pyramids can both contain faces that are triangles. In a pyramid, all triangular faces that are not the base meet at a one vertex and have shared edges. In a prism, there can be a triangular base, but the other faces are quadrilaterals.
Activity Synthesis
Invite a few students to share their matching decisions and reasoning with the class. Ask students: “What clues did you use to help you match? How did you check if you were right?” If there is not unanimous agreement on any of the nets, ask students with differing opinions to explain their reasoning. Discuss to come to an agreement.
14.2: Using Nets to Find Surface Area (25 minutes)
Activity
In this activity, students cut and assemble nets into polyhedra and learn to use nets to find surface area. The presence of a grid supports students in their calculations. It also reinforces the idea of area as the number of unit squares in a region and the connection between area and surface area. Students apply what they learned earlier about areas of triangles and parallelograms to find surface area.
As students make calculations, monitor their processes. Note those who work systematically to find surface area (e.g., by organizing the measurements of each face, calculating the area of each face, and adding the areas together) and those who don't. Encourage students with disorganized or scattered work to take a more systematic approach. Demonstrate strategies such as labeling both the polygons on the net and portions of their work that pertain to those faces.
Also notice students who look for and use structure (MP7), for instance, by grouping certain polygons together and finding the area of the composite shape (e.g., a group of rectangles that have a common side length), or by identifying multiple copies of the same polygon and calculating the area once. Select them to share their work later.
Launch
Arrange students in groups of 3. Give each group one of each net (A, B, and C), tape, and access to their geometry toolkits (especially scissors). Explain to students that they will cut some nets, assemble them into polyhedra, and calculate their surface areas. Remind students that the surface area of a three-dimensional figure is the sum of the areas of all of its faces. Ask students to complete the first question before cutting anything.
Point out that the net has shaded and unshaded polygons. Explain that only the shaded polygons in the nets will show once the net is assembled. The unshaded polygons are “flaps” to make it easier to glue or tape the polygons together. They will get tucked behind the shaded polygons and are not really part of the polyhedron. Tell students that creasing along all of the lines first will make it easier to fold the net up and attach the various polygons together. A straightedge can be very helpful for making the creases.
Tell students that it is easy to miss or double-count the area of a face when finding surface area. Ask them to think carefully about how to record their calculations to ensure that all faces are accounted for, correct measurements are used, and errors are minimized.
When students have completed their calculations, ask them to compare and discuss their work with another student with the same polyhedron.
Supports accessibility for: Visual-spatial processing; Fine-motor skills
Student Facing
-
Name the polyhedron that each net would form when assembled.
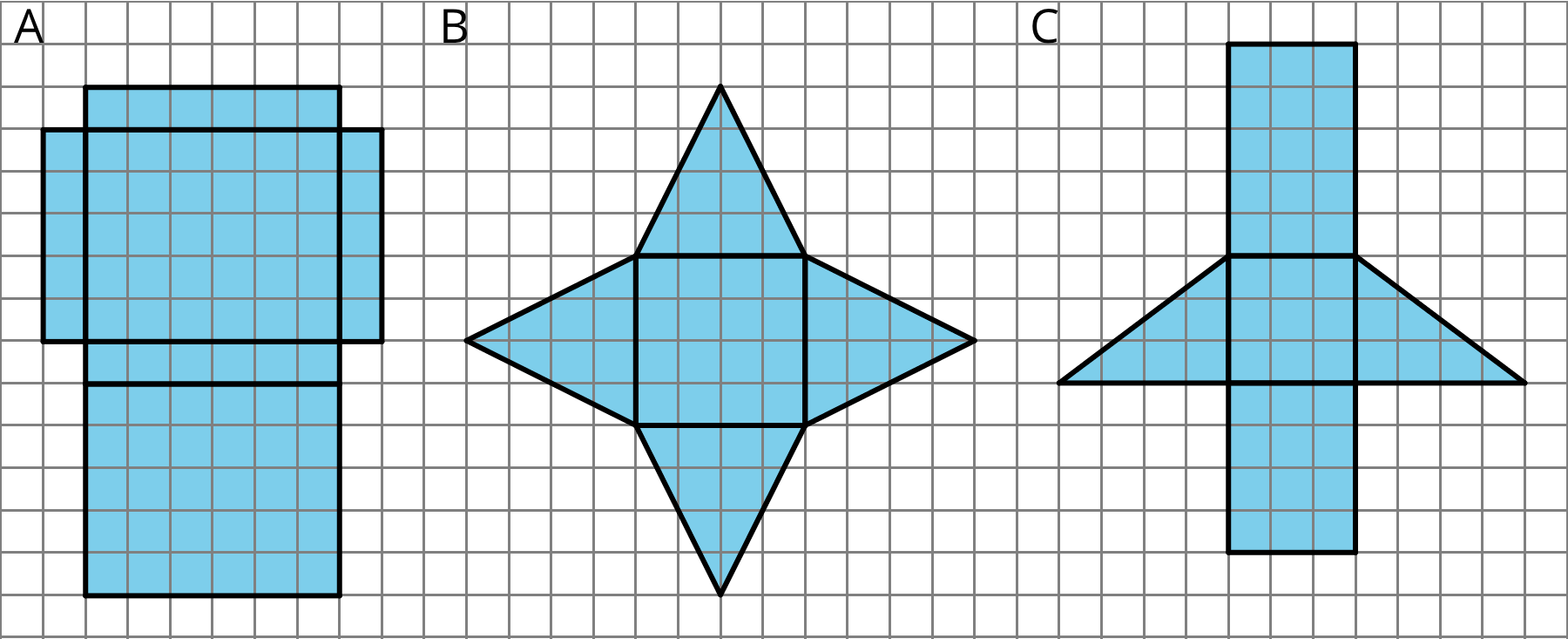
- Your teacher will give you the nets of three polyhedra. Cut out the nets and assemble the three-dimensional shapes.
- Find the surface area of each polyhedron. Explain your reasoning clearly.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
-
For each net, decide if it can be assembled into a rectangular prism.
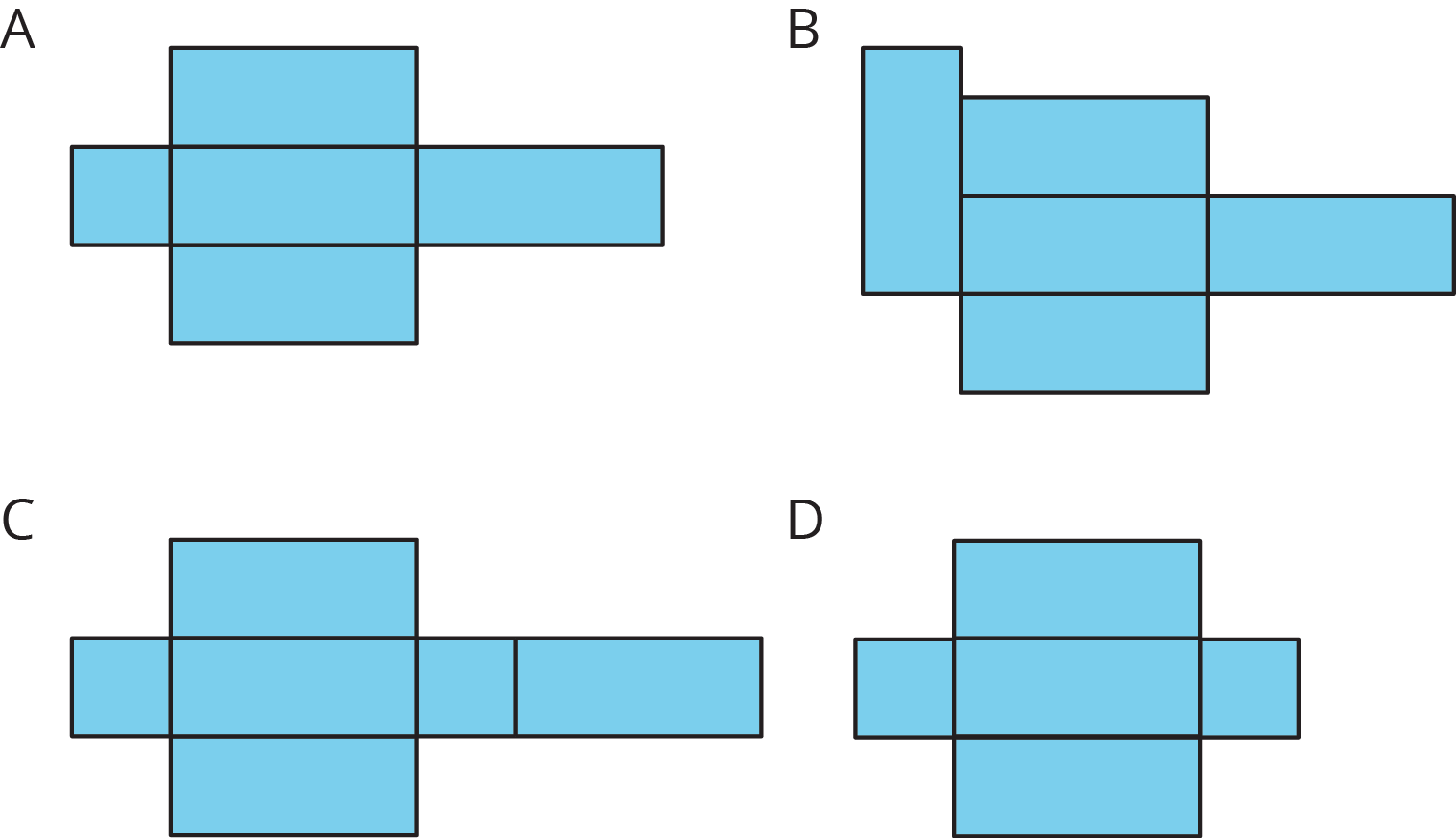
-
For each net, decide if it can be folded into a triangular prism.
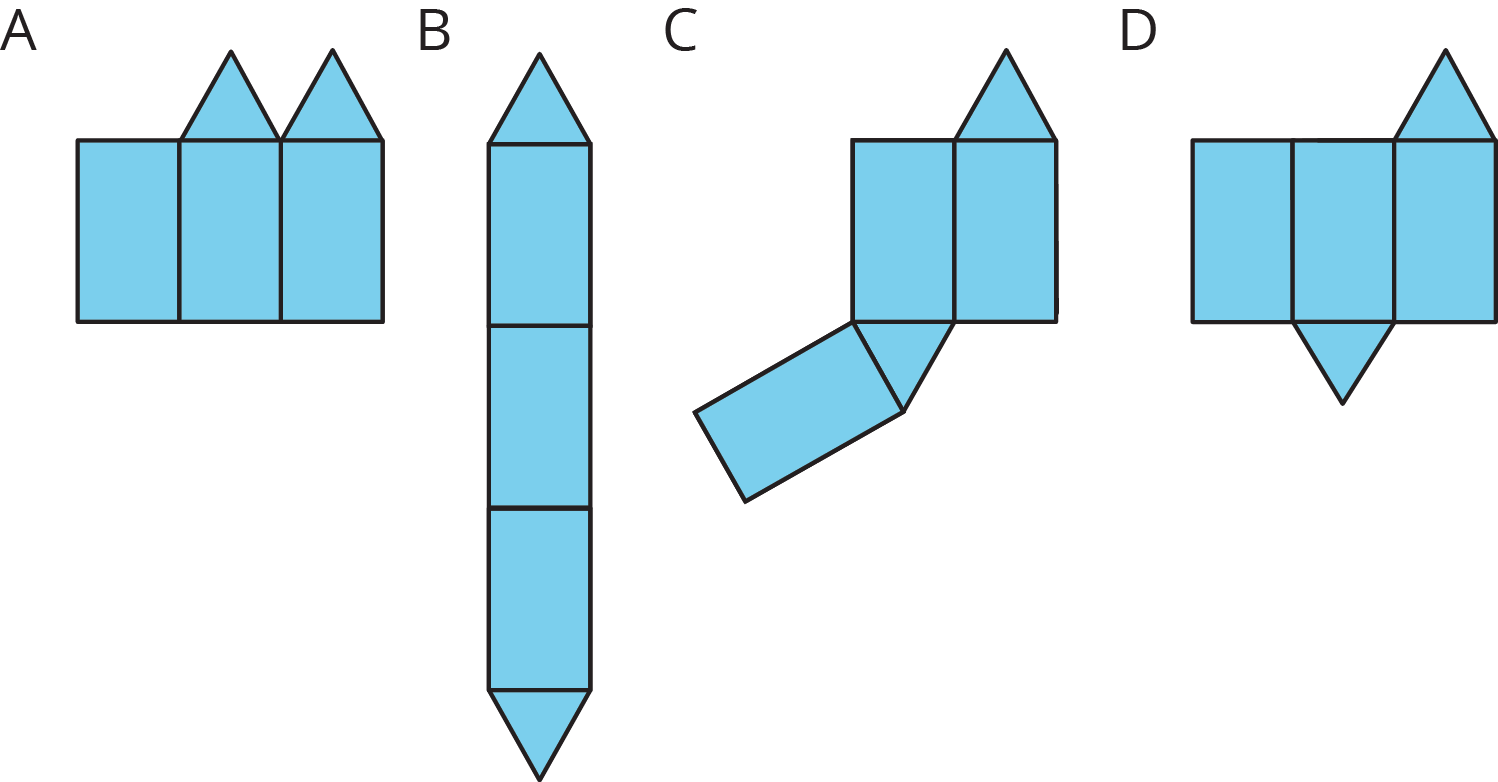
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students do not identity the specific type of prism or pyramid, remind them that they should also name each figure by the shape of their base.
Activity Synthesis
For each polyhedron, select at least 2 students with correct calculations but different approaches to share their work, if possible.
For Polyhedron A, select students who took the following approaches, in this sequence:
- Found the area of each rectangle separately
- Found the areas of pairs of identical rectangles (3 pairs total)
- Calculated the area of a group of connected rectangles with the same length or width (e.g., the four rectangles on the net with side length 6 units)
For Polyhedron B, select students who:
- Found the area of each of the 5 polygons separately
- Found the area of the square, rearranged the 4 triangles into 2 parallelograms, and calculated the area of each parallelogram
- Calculated the area of the square and the area of 1 triangle, and multiplying the area of the triangle by 4
For Polyhedron C, select students who:
- Found the area of each of the 5 polygons separately
- Rearranged the 2 right triangles into a rectangle, and then found the area of each rectangle separately
- Calculated the area of each right triangle and doubled it, and found the area of the group of connected rectangles with a width of 4 units
Point out that the reasoning strategies we used earlier in the unit still apply here. Even though we are working with three-dimensional figures, surface area is a two-dimensional measure.
Highlight the benefits of approaching the problems systematically, e.g., by labeling parts, listing measurements and computations in order, etc.
Design Principle(s): Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
In this lesson, we matched nets to the polyhedra, assembled polyhedra from nets, and used nets to find surface area. Discuss:
-
“How do we use a net to find surface area?” (We calculate the area of each polygon on the net and add all the areas.)
-
“How is finding surface area using a net different from finding surface area by looking at a picture of a polyhedron—as we had done with the filing cabinet, or by studying the actual object—as we had done with the snap cubes?” (A net allows us to see all the faces of a polyhedron at once. When working from a picture or drawing, we need to visualize the hidden faces. Working with an actual polyhedron could help, but again we are not looking at all the faces at once; we have to rotate the object and might miss or double-count a face.)
-
“When using a net, how do we keep track of your calculations or make sure all faces are accounted for?” (We can label all the polygons and the calculations.)
-
“Are there ways to simplify the calculations? Or is it best to find the area of each polygon one at a time?” (Sometimes we can simplify the process by combining polygons and finding the area of the combined region—e.g., a group of rectangles with the same side length. If there are several polygons that are identical, we can find the area of one polygon and multiply it by the number of identical polygons in the net.)
14.3: Cool-down - Unfolded (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
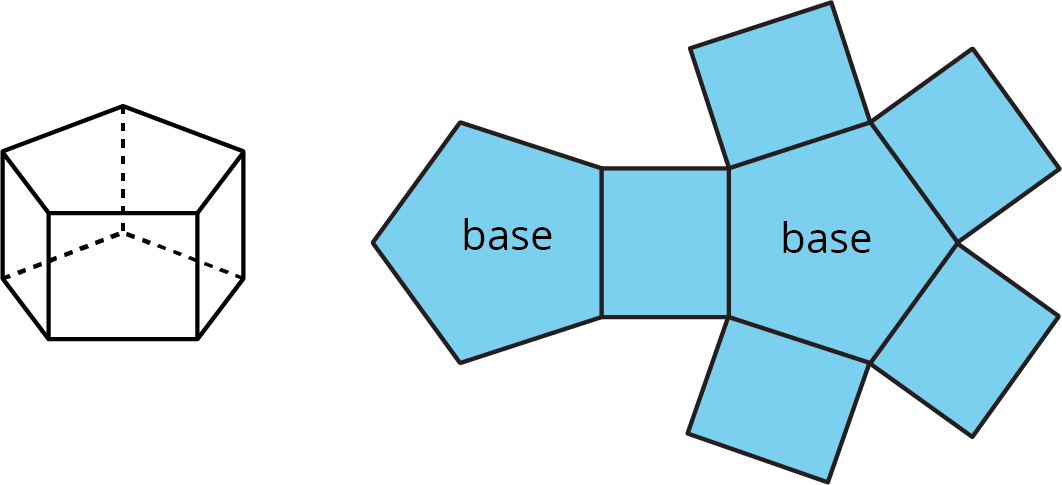
A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A pentagonal pyramid and its net are shown here.

A net of a prism has two copies of the polygon that is the base. The rest of the polygons are rectangles. A pentagonal prism and its net are shown here.
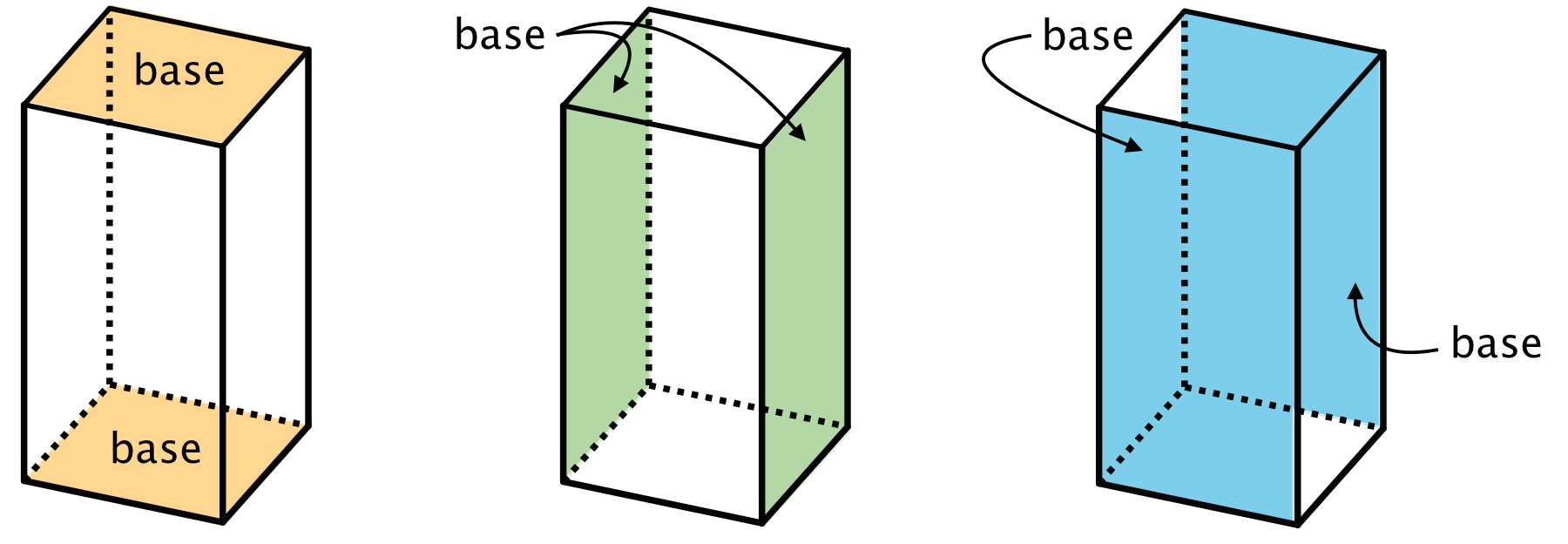
In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases.
Because a net shows all the faces of a polyhedron, we can use it to find its surface area. For instance, the net of a rectangular prism shows three pairs of rectangles: 4 units by 2 units, 3 units by 2 units, and 4 units by 3 units.
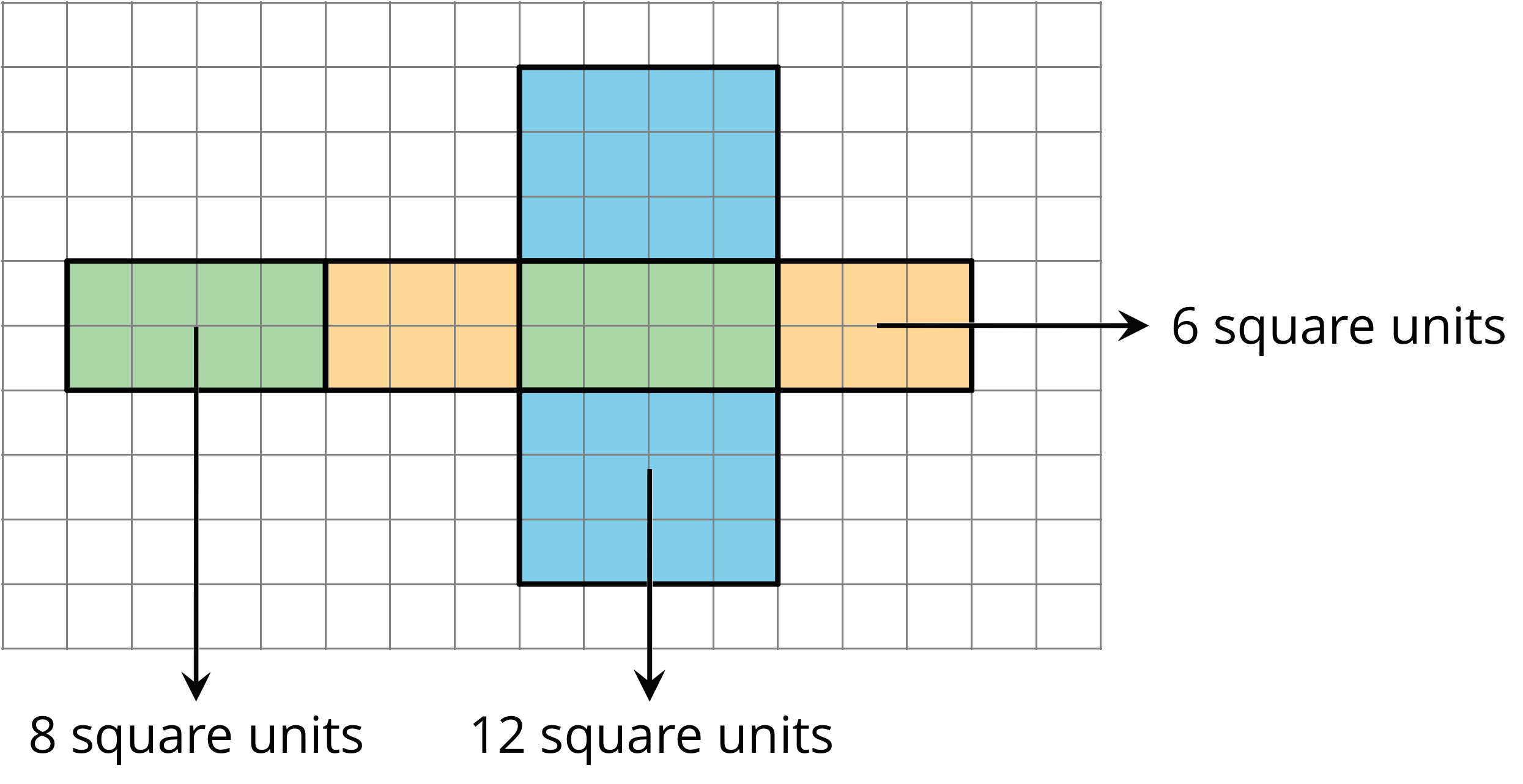
The surface area of the rectangular prism is 52 square units because \(8+8+6+6+12+12=52\).