Lesson 15
More Nets, More Surface Area
15.1: Notice and Wonder: Wrapping Paper (5 minutes)
Warm-up
This warm-up prompts students to think about a prism and its measurements in context and to consider potential questions that could be asked and answered.
Given their recent work, students are likely to notice and wonder about surface area, nets, and the missing height of the box. Students may also wonder about the volume of the box, given their geometric work in grade 5.
When prompted about how to find the surface area or the volume of the box, students will likely ask about the missing measurement. This is an opportunity for them to practice making a reasonable estimate.
Launch
Arrange students in groups of 2. Give students a minute of quiet time to observe the image. Ask students to be prepared to share at least one thing they notice and one thing they wonder about the picture. Ask them to give a signal when they have noticed or wondered about something.
Student Facing
Kiran is wrapping this box of sports cards as a present for a friend.
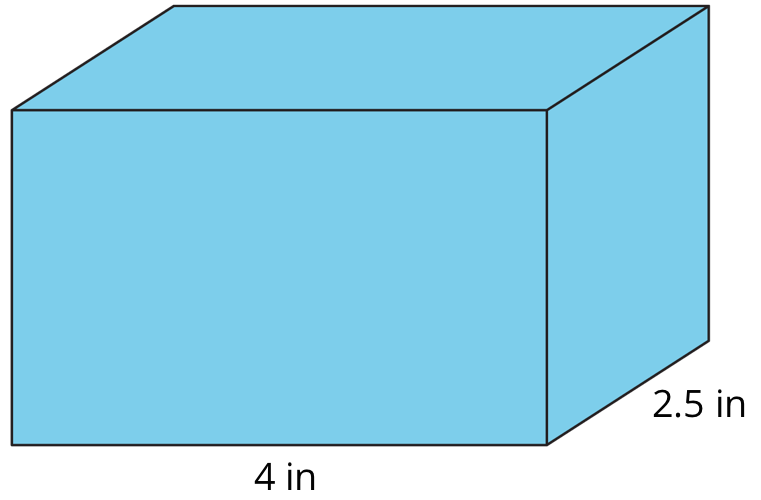
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share their observations and questions. Record the responses for all to see. If no students wonder about the surface area, the amount of wrapping paper needed, or the volume of the box, bring these questions up.
Tell students to choose either a question about surface area or one about volume and give them a minute to discuss with a partner how they would find the answer to the question. If students suggest that it cannot be done because of missing information, ask them to estimate the missing information.
Select a couple of students to share how they would find the surface area or the volume of the given box. After each response, poll the class on whether they agree or disagree.
15.2: Building Prisms and Pyramids (30 minutes)
Activity
Previously, students used a given net of a polyhedron to find its surface area. Here they use a given polyhedron to draw a net and then calculate its surface area.
Use the provided polyhedra to differentiate the work for students with varying degrees of visualization skills. Rectangular prisms (A and C), triangular prisms (B and D), and square pyramids (F and G) can be managed by most students. Triangular Prism E requires a little more interpretive work (i.e., the measurements of some sides may not be immediately apparent to students). Trapezoidal Prism H and Polyhedron I (a composite of a cube and a square pyramid) require additional interpretation and reasoning.
As students work, remind them of the organizational strategies discussed in previous lessons, i.e., labeling polygons, showing measurements on the net, etc.

Launch
Arrange students in groups of 2–3. Give each student in the group a different polyhedron from the blackline master and access to their geometry toolkits. Students need graph paper and a straightedge from their toolkits.
Explain to students that they will draw a net, find its surface area, and have their work reviewed by a peer. Give students 4–5 minutes of quiet time to draw their net on graph paper and then 2–3 minutes to share their net with their group and get feedback. When the group is sure that each net makes sense and all polygons of each polyhedron are accounted for, students can proceed and use the net to help calculate surface area.
If time permits, prompt students to cut and assemble their net into a polyhedron. Demonstrate how to add flaps to their net to accommodate gluing or taping. There should be as many flaps as there are edges in the polyhedron. (Remind students that this is different than the number of edges in the polygons of the net.)
Supports accessibility for: Visual-spatial processing; Organization
Student Facing
Your teacher will give you a drawing of a polyhedron. You will draw its net and calculate its surface area.
-
What polyhedron do you have?
-
Study your polyhedron. Then, draw its net on graph paper. Use the side length of a grid square as the unit.
-
Label each polygon on the net with a name or number.
-
Find the surface area of your polyhedron. Show your thinking in an organized manner so that it can be followed by others.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may know what polygons make up the net of a polyhedron but arrange them incorrectly on the net (i.e., when cut and assembled the faces overlap instead of meeting at shared edges, or the faces are oriented incorrectly or are in the wrong places). Suggest that students label some faces of the polyhedron drawing and transfer the adjacencies they see to the net. If needed, demonstrate the reasoning (e.g., “Face 1 and face 5 both share the edge that is 7 units long, so I can draw them as two attached rectangles sharing a side that is 7-unit long.”)
It may not occur to students to draw each face of the polyhedron to scale. Remind them to use the grid squares on their graph paper as units of measurement.
If a net is inaccurate, this becomes more evident when it is being folded. This may help students see which parts need to be adjusted and decide the best locations for the flaps. Reassure students that a few drafts of a net may be necessary before all the details are worked out, and encourage them to persevere (MP1).
Activity Synthesis
Ask students who finish their calculation to find another person in the class with the same polyhedron and discuss the following questions (displayed for all to see):
- Do your calculations match? Should they?
- Do your nets result in the same polyhedra? Should they?
- Do your models match the picture you were given? Why or why not?
If time is limited, consider having the answer key posted somewhere in the classroom so students could quickly check their surface area calculations.
Reconvene briefly for a whole-class discussion. Invite students to reflect on the process of drawing a net and finding surface area based on a picture of a polyhedron. Ask questions such as:
- How did you know that your net show all the faces of your polyhedron?
- How did you know where to put each polygon or how to arrange all polygons so that, if folded, they can be assembled into the polyhedron in the drawing?
- How did the net help you find surface area?
Design Principle(s): Cultivate conversation; Maximize meta-awareness
15.3: Comparing Boxes (15 minutes)
Optional activity
In this activity, students compare the surface areas and volumes of three rectangular prisms given nets that are not on a grid. To do this, they need to be able to visualize the three-dimensional forms that the two-dimensional nets would take when folded.
In grade 5, students had learned to distinguish area and volume as measuring different attributes. This activity clarifies and reinforces that distinction.
Launch
Keep students in the same groups of 2–3. Tell students that this activity involves working with both volume and surface area. To refresh students' understanding of volume from grade 5, ask students:
- “When we find the volume of a prism, what are we measuring?”
- “How is volume different than surface area?”
- “How might we find the volume of a rectangular prism?”
Reiterate that volume measures the number of unit cubes that can be packed into a three-dimensional shape and that we can find the number of unit cubes in a rectangular prism by multiplying the side lengths of a prism.
Give students 1–2 minutes to read the task statement and questions. Ask them to think about how they might go about answering each question and to be prepared to share their ideas. Give students a minute to discuss their ideas with their group. Then, ask groups to collaborate: each member should perform the calculations for one prism (A, B, or C). Give students 5–7 minutes of quiet time to find the surface area and volume for their prism and then additional time to compare their results and answer the questions.
Supports accessibility for: Language; Organization
Student Facing
Here are the nets of three cardboard boxes that are all rectangular prisms. The boxes will be packed with 1-centimeter cubes. All lengths are in centimeters.
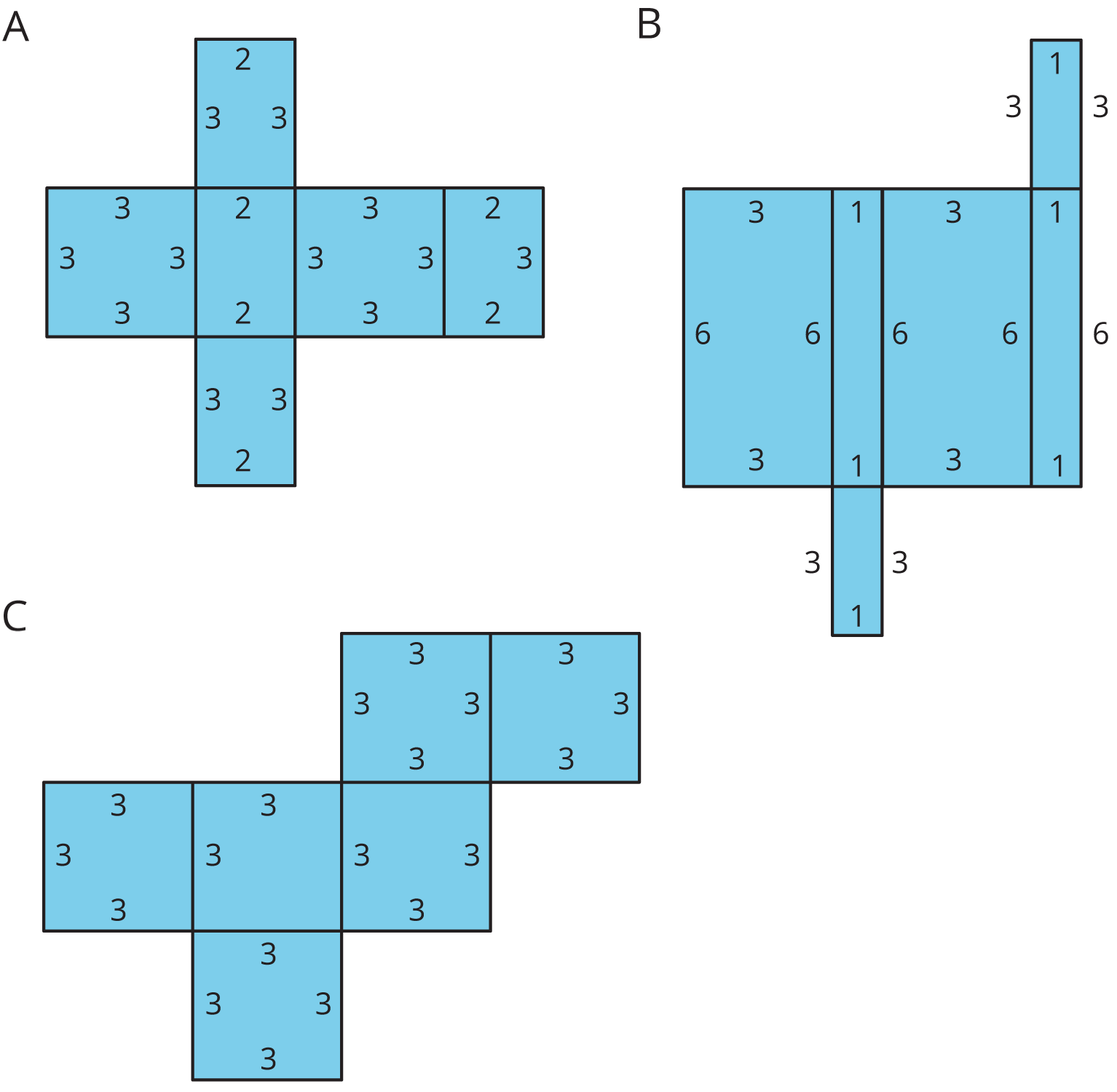
- Compare the surface areas of the boxes. Which box will use the least cardboard? Show your reasoning.
- Now compare the volumes of these boxes in cubic centimeters. Which box will hold the most 1-centimeter cubes? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Figure C shows a net of a cube. Draw a different net of a cube. Draw another one. And then another one. How many different nets can be drawn and assembled into a cube?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students should have little trouble finding areas of rectangles but may have trouble keeping track of pairs of measurements to multiply and end up making calculation errors. Suggest that they label each polygon in the net and the corresponding written work and double-check their calculations to minimize such errors.
If students struggle to find the volume of their prism using information on a net, suggest that they sketch the prism that can be assembled from the net and label the edges of the prism.
Students may need a reminder that area is measured in square units and volume is measured in cubic units.
Activity Synthesis
Select a few students to share the surface area and volume of each prism. After each person shares, poll those who worked on the same prism for agreement or disagreement. Record the results on the board.
Invite students to share a few quick observations about the relationship between the surface areas and volumes for these three prisms, or between the amounts of material needed to build the boxes and the number of cubes that they can contain. Discuss questions such as:
- “If these prisms are boxes, which prism—B or C—would take more material to build? Which can fit more unit cubes?” (B and C would likely take the same amount of material to build since their surface areas are the same. C has a greater volume than B, so it can fit more unit cubes.)
- “Which prism—A or B—would take more material to build? Which can fit more unit cubes?” (A and B can fit the same number of unit cubes but, B would require more material to build.)
- “If two prisms have the same surface area, would they also have the same volume? How do you know?” (No, prisms A, B, and C are examples of how two figures with the same volume may not have the same surface area, and vice versa.)
Students will gain more insights into these ideas as they explore squares, cubes, and exponents in upcoming lessons. If students could benefit from additional work on distinguishing area and volumes as different measures, do the optional lesson Distinguishing Between Surface Area and Volume.
Design Principle(s): Optimize output (for justification); Support sense-making
Lesson Synthesis
Lesson Synthesis
To highlight some key points from the lesson, display a picture of a prism or a pyramid and a drawing of its net. Discuss these questions:
-
“Can you find the surface area of a simple prism or pyramid from a picture, if all the necessary measurements are given?”
-
“Can you find the surface area from a net, if all the measurements are given?”
-
“Which might be more helpful for calculating surface area—a picture of a polyhedron or a net?” (If the polyhedron is simple—e.g., a cube, a square pyramid, etc.—and does not involve hidden faces with different measurements or require a lot of visualizing, either a picture or a net can work. Otherwise, a net may be more helpful because we can see all of the faces at once and can find the area of each polygon more easily. A net may also help us keep track of our calculations and notice missing or extra areas.)
15.4: Cool-down - Surface Area of a Triangular Prism (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The surface area of a polyhedron is the sum of the areas of all of the faces. Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.
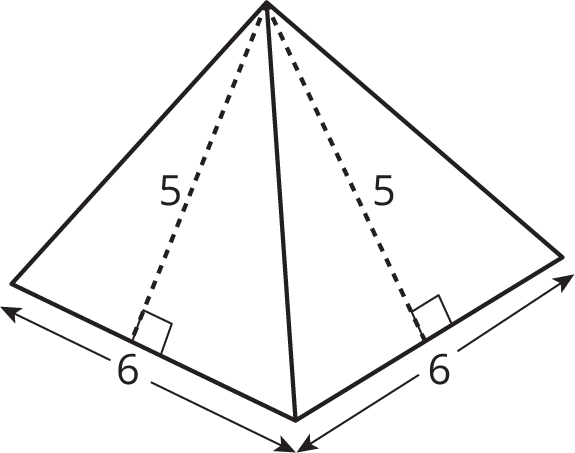
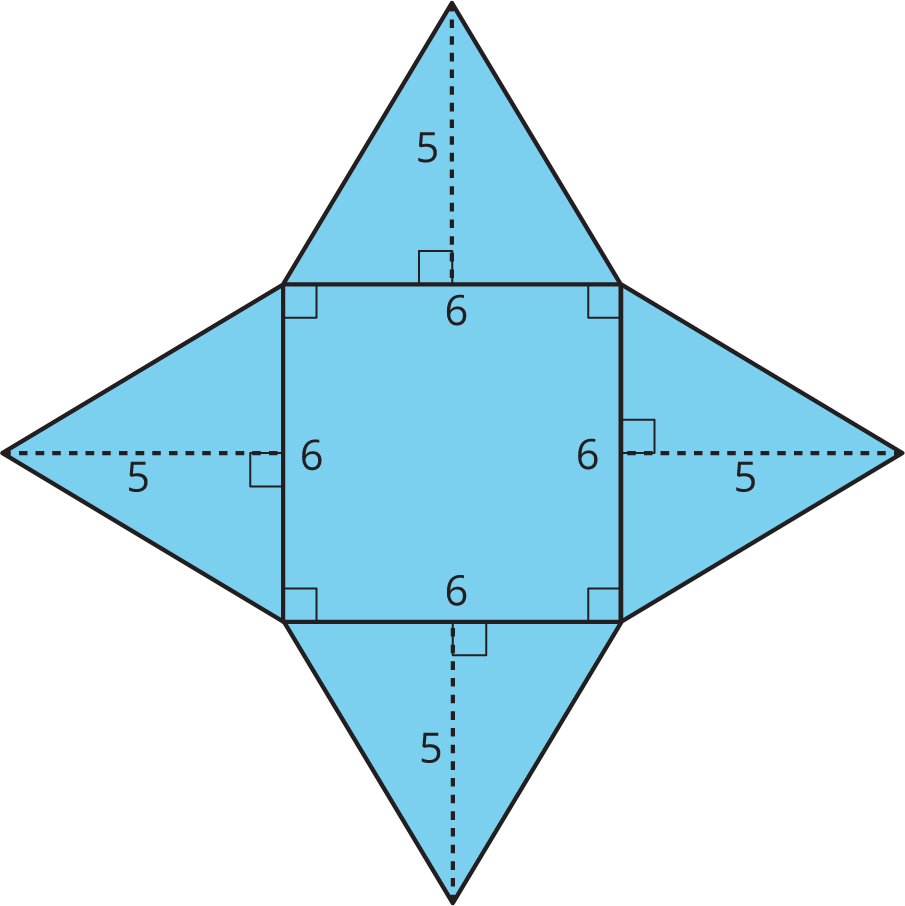
A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces:
\((6\boldcdot 6) + 4\boldcdot \left(\frac12 \boldcdot 5 \boldcdot 6\right) = 96\)
The surface area of this square pyramid is 96 square units.