Lesson 9
Formula for the Area of a Triangle
9.1: Bases and Heights of a Triangle (10 minutes)
Warm-up
In this activity, students think about the meaning of base and height in a triangle by studying examples and non-examples. The goal is for them to see that in a triangle:
- Any side can be a base.
- A segment that represents a height must be drawn at a right angle to the base, but can be drawn in more than one place. The length of this perpendicular segment is the distance between the base and the vertex opposite it.
- A triangle can have three possible bases and three corresponding heights.
Students may draw on their experience with bases and heights in a parallelogram and observe similarities. Encourage this, as it would help them conceptualize base-height pairs in triangles.
As students discuss with their partners, listen for how they justify their decisions or how they know which statements are true (MP3).
Launch
Display the examples and non-examples of bases and heights for all to see. Give students a minute to observe them. Ask them to be ready to share at least one thing they notice and one thing they wonder. Give the class a minute to share some of their observations and questions.
Tell students they will now use the examples and non-examples to determine what is true about bases and heights in a triangle. Arrange students in groups of 2. Give them 2–3 minutes of quiet think time and then a minute to to share their response with a partner.
Student Facing
Study the examples and non-examples of bases and heights in a triangle.
- Examples: These dashed segments represent heights of the triangle.

- Non-examples: These dashed segments do not represent heights of the triangle.
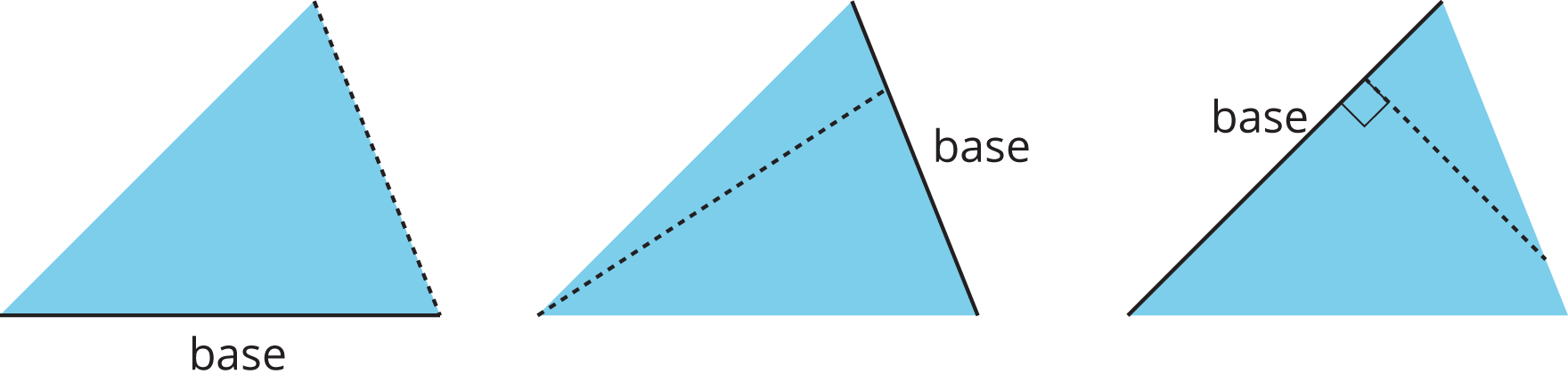
Select all the statements that are true about bases and heights in a triangle.
- Any side of a triangle can be a base.
- There is only one possible height.
- A height is always one of the sides of a triangle.
- A height that corresponds to a base must be drawn at an acute angle to the base.
- A height that corresponds to a base must be drawn at a right angle to the base.
- Once we choose a base, there is only one segment that represents the corresponding height.
- A segment representing a height must go through a vertex.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may struggle to interpret the diagrams. Ask them to point out parts of the diagrams that might be unclear and clarify as needed.
Students may not remember from their experience with parallelograms that a height needs to be perpendicular to a base. Consider posting a diagram of a parallelogram—with its base and height labeled—in a visible place in the room so that it can serve as a reference.
Activity Synthesis
For each statement, ask students to indicate whether they think it is true. For each “true” vote, ask one or two students to explain how they know (MP3). Do the same for each “false” vote. Encourage students to use the examples and counterexamples to support their argument (e.g., "The last statement is not true because the examples show dashed segments or heights that do not go through a vertex.") which means more than one height." Agree on the truth value of each statement before moving on. Record and display the true statements for all to see.
Students should see that only statements 1 and 5 are true—that any side of a triangle can be a base, and a segment for the corresponding height must be drawn at a right angle to the base. What is missing—an important gap to fill during discussion—is the length of any segment representing a height.
Ask students, “How long should a segment that shows a height be? If we draw a perpendicular line from the base, where do we stop?” Solicit some ideas from students.
Explain that the length of each perpendicular segment is the distance between the base and the vertex opposite of it. The opposite vertex is the vertex that is not an endpoint of the base. Point out the opposite vertex for each base. Clarify that the segment does not have to be drawn through the vertex (although that would be a natural place to draw it), as long as it maintains that distance between the base and the opposite vertex.
It is helpful to connect this idea to that of heights in a parallelogram. Consider duplicating the triangle and use the original and the copy to compose a parallelogram. The height for a chosen base in the triangle is also the height of the parallelogram with the same base.
Students will have many opportunities to make sense of bases and heights in this lesson and an upcoming one, so they do not need to know how to draw a height correctly at this point.
9.2: Finding a Formula for Area of a Triangle (20 minutes)
Activity
This task culminates in writing a formula for the area of triangles. By now students are likely to have developed the intuition that the area of a triangle is half of that of a parallelogram with the same base and height. This activity encapsulates that work in an algebraic expression.
Students first find the areas of several triangles given base and height measurements. They then generalize the numerical work to arrive at an expression for finding the area of any triangle (MP8).
If needed, remind students how they reasoned about the area of triangles in the previous lesson (i.e. by composing a parallelogram, enclosing with one or more rectangles, etc.). Encourage them to refer to their previous work and use tracing paper as needed. Students might write \(b \boldcdot h \div 2\) or \(b \boldcdot h \boldcdot \frac12\) as the expression for the area of any triangle. Any equivalent expression should be celebrated.
At the end of the activity, consider giving students a chance to reason more abstractly and deductively, i.e., to think about why the expression \(b \boldcdot h \div 2\) would hold true for all triangles. See Activity Synthesis for prompts and diagrams that support such reasoning.
Launch
Arrange students in groups of 2–3. Explain that they will now find the area of some triangles using what they know about base-height pairs in triangles and the relationships between triangles and parallelograms.
Give students 5–6 minutes to complete the activity and access to geometry toolkits, especially tracing paper. Ask them to find the area at least a couple of triangles independently before discussing with their partner(s).
Student Facing
For each triangle:
- Identify a base and a corresponding height, and record their lengths in the table.
- Find the area of the triangle and record it in the last column of the table.
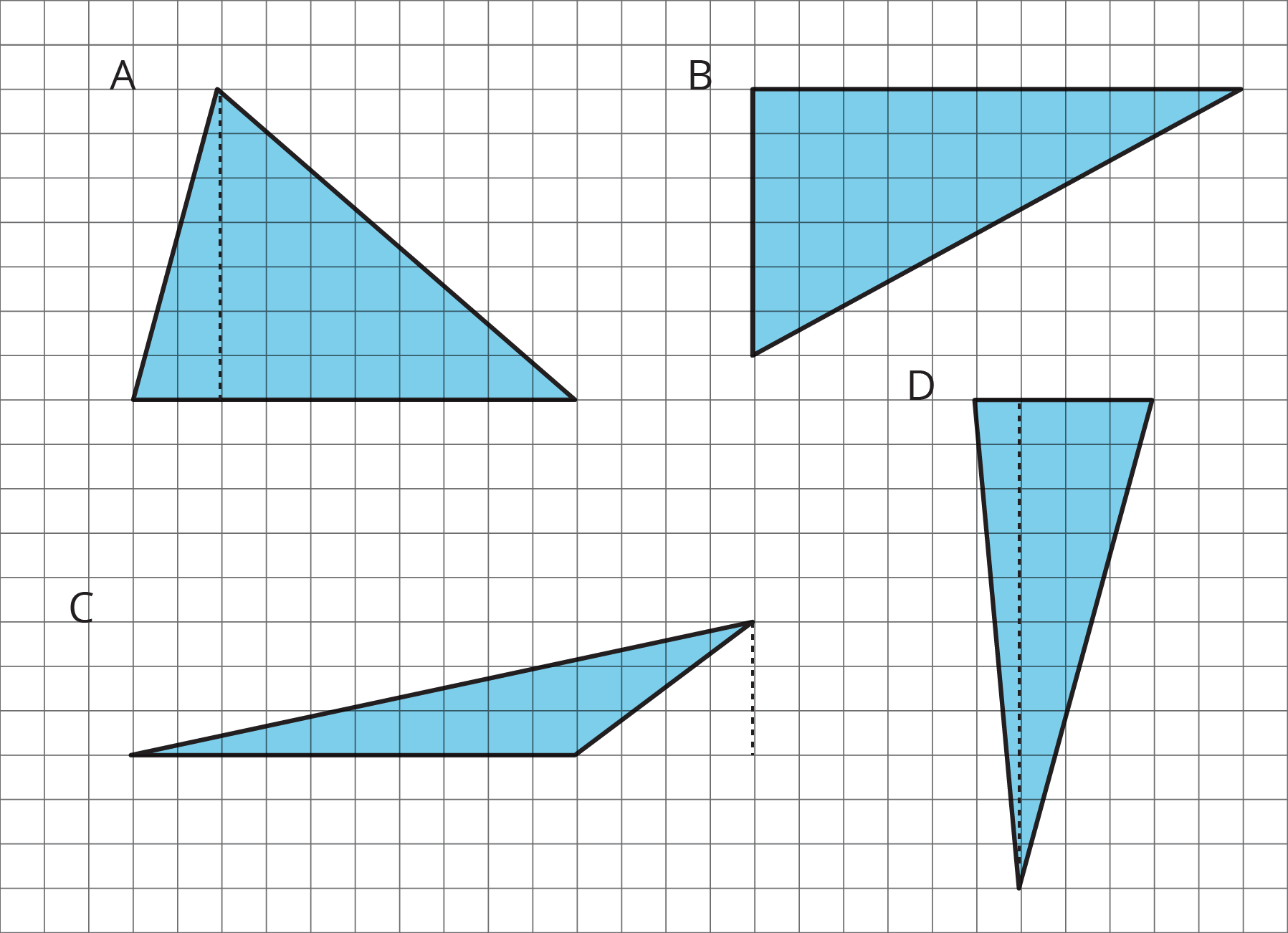
| triangle | base (units) | height (units) | area (square units) |
|---|---|---|---|
| A | |||
| B | |||
| C | |||
| D | |||
| any triangle | \(b\) | \(h\) |
In the last row, write an expression for the area of any triangle, using \(b\) and \(h\).
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not be inclined to write an expression using the variables \(b\) and \(h\) and instead replace the variables with numbers of their choice. Ask them to reflect on what they did with the numbers for the first four triangles. Then, encourage them to write the same operations but using the letters \(b\) and \(h\) rather than numbers.
Activity Synthesis
Select a few students to share their expression for finding the area of any triangle. Record each expression for all to see.
To give students a chance to reason logically and deductively about their expression, ask, “Can you explain why this expression is true for any triangle?”
Display the following diagrams for all to see. Give students a minute to observe the diagrams. Ask them to choose one that makes sense to them and use that diagram to explain or show in writing that the expression \(b \boldcdot h \div 2\) works for finding the area of any triangle. (Consider giving each student an index card or a sheet of paper on which to write their reasoning so that their responses could be collected, if desired.)
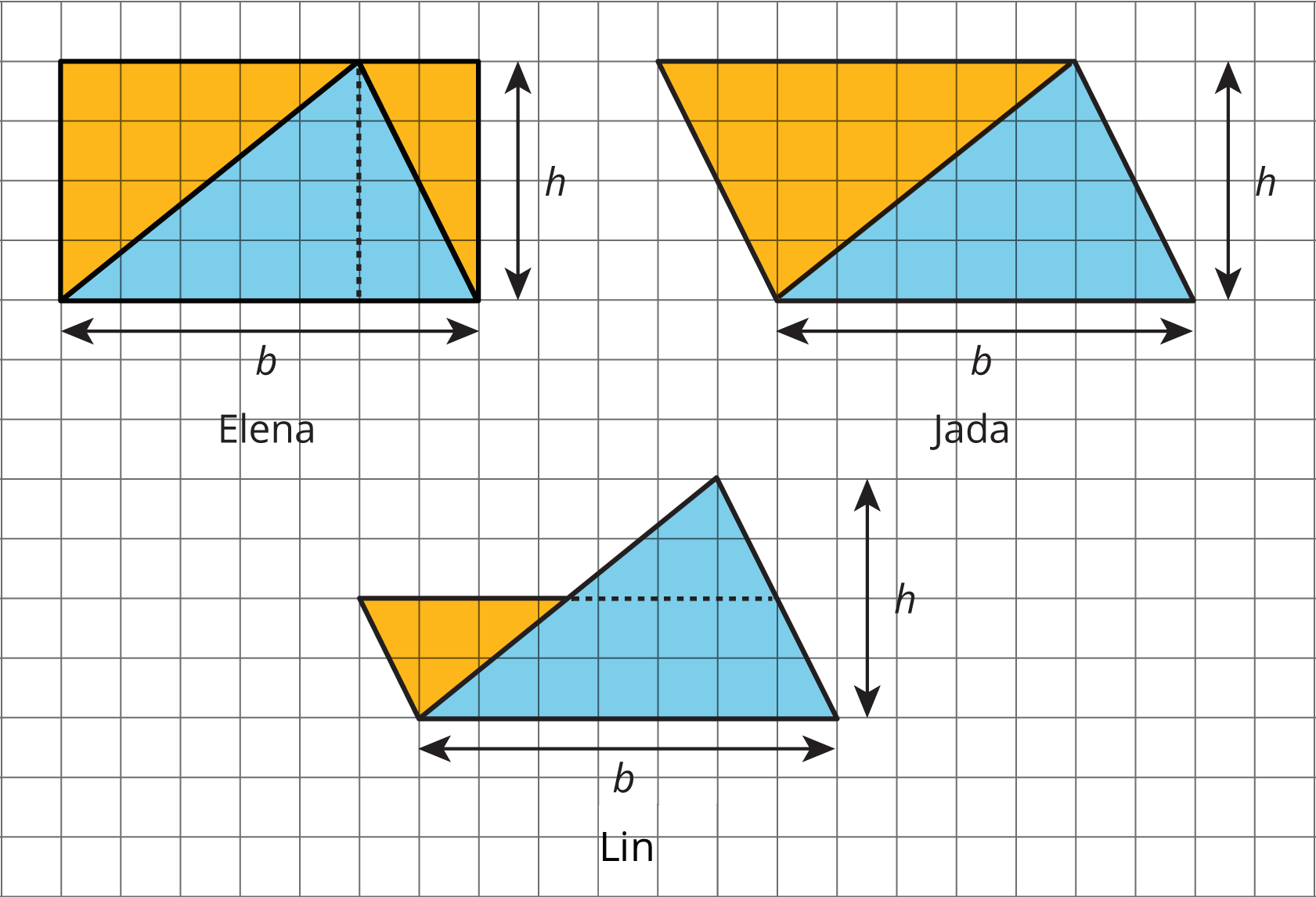
When dealing only with the variables \(b\) and \(h\) and no numbers, students are likely to find Jada's and Lin's diagrams more intuitive to explain. Those choosing to use Elena's diagram are likely to suggest moving one of the extra triangles and joining it with the other to form a non-rectangular parallelogram with an area of \(b \boldcdot h\). Expect students be less comfortable reasoning in abstract terms than in concrete terms. Prepare to support them in piecing together a logical argument using only variables.
If time permits, select students who used different diagrams to share their explanation, starting with the most commonly used diagram (most likely Jada's). Ask other students to support, refine, or disagree with their arguments. It time is limited, consider collecting students' written responses now and discussing them in an upcoming lesson.
Supports accessibility for: Memory; Language
Design Principle(s): Support sense-making; Maximize meta-awareness
9.3: Applying the Formula for Area of Triangles (10 minutes)
Activity
In this activity, students apply the expression they previously generated to find the areas of various triangles. Each diagram is labeled with two or three measurements. Before calculating, students think about which lengths can be used to find the area of each triangle.
As students work, notice students who choose different bases for Triangles B and D. Invite them to contribute to the discussion about finding the areas of right triangles later.
Launch
Explain to students that they will now practice using their expression to find the area of triangles without a grid. For each triangle, ask students to be prepared to explain which measurement they choose for the base and which one for the corresponding height and why.
Keep students in groups of 2–4. Give students 5 minutes of quiet think time, followed by 1–2 minutes for discussing their responses in their group.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
For each triangle, circle a base measurement that you can use to find the area of the triangle. Then, find the area of any three triangles. Show your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The extra measurement in Triangles C, D, and E may confuse some students. If they are unsure how to decide the measurement to use, ask what they learned must be true about a base and a corresponding height in a triangle. Urge them to review the work from the warm-up activity.
Activity Synthesis
The aim of this whole-class discussion is to deepen students’ awareness of the base and height of triangles. Discuss questions such as:
- For Triangle A, can we say that the 6-cm segment is the base and the 5-cm segment is the height? Why or why not? (No, the base of a triangle is one of its sides.)
- What about for Triangle C: Can the 3-cm segment serve as the base? Why or why not? (No, that segment is not a side of the triangle.)
- Can the 3.5-cm side in Triangle C serve as the base? Why or why not? (Yes, it is a side of the triangle, but because we don't have the height that corresponds to it, it is not helpful for finding the area here.)
- More than two measurements are given for Triangles C, D, and E. Which ones are helpful for finding area? (We need a base and a corresponding height, which means the length of one side of the triangle and the length of a perpendicular segment between that side and the opposite vertex.)
- When it comes to finding area, how are right triangles—like B and D—unique? (Either of the two sides that form the right angle could be the base or the height. In non-right triangles—like A, C, and E—the height segment is not a side of the triangle; a different line segment has to be drawn.)
Lesson Synthesis
Lesson Synthesis
The area of a parallelogram can be determined using base and height measurements. In this lesson you learned that we can do the same with triangles.
- “How do we locate the base of a triangle? How many possible bases are there?” (Any side of a triangle can be a base. There are 3 possible bases.)
- “How do we locate the height once we know the base?” (Find the length of a perpendicular segment that connects the base and its opposite vertex.)
We can use the base-height pair of measurements to find the area of a triangle quite simply.
- “What expression works for finding the area of a triangle?” (\(\frac12 \boldcdot b \boldcdot h\) or \(\frac {b \boldcdot h}{2}\))
- “Can you explain briefly why this expression or formula works?” (The area of a triangle is always half of the area of a related parallelogram that shares the same base and height.)
You learned that any side of the triangle can be the base, but not all sides can be the height.
- “Are there cases in which both the base and the height are sides of the triangle? When does that happen?” (Yes. In a right triangle, both the base and height can be the sides of the triangle.)
9.4: Cool-down - Two More Triangles (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
- We can choose any of the three sides of a triangle to call the base. The term “base” refers to both the side and its length (the measurement).
- The corresponding height is the length of a perpendicular segment from the base to the vertex opposite of it. The opposite vertex is the vertex that is not an endpoint of the base.
Here are three pairs of bases and heights for the same triangle. The dashed segments in the diagrams represent heights.

A segment showing a height must be drawn at a right angle to the base, but it can be drawn in more than one place. It does not have to go through the opposite vertex, as long as it connects the base and a line that is parallel to the base and goes through the opposite vertex, as shown here.
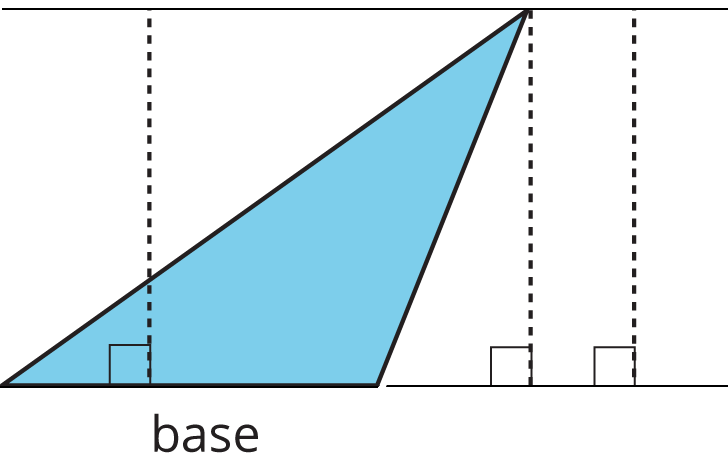
The base-height pairs in a triangle are closely related to those in a parallelogram. Recall that two copies of a triangle can be composed into one or more parallelograms. Each parallelogram shares at least one base with the triangle.

For any base that they share, the corresponding height is also shared, as shown by the dashed segments.
We can use the base-height measurements and our knowledge of parallelograms to find the area of any triangle.
- The formula for the area of a parallelogram with base \(b\) and height \(h\) is \(b \boldcdot h\).
- A triangle takes up half of the area of a parallelogram with the same base and height. We can therefore express the area \(A\) of a triangle as: \(\displaystyle A = \frac12 \boldcdot b \boldcdot h\)
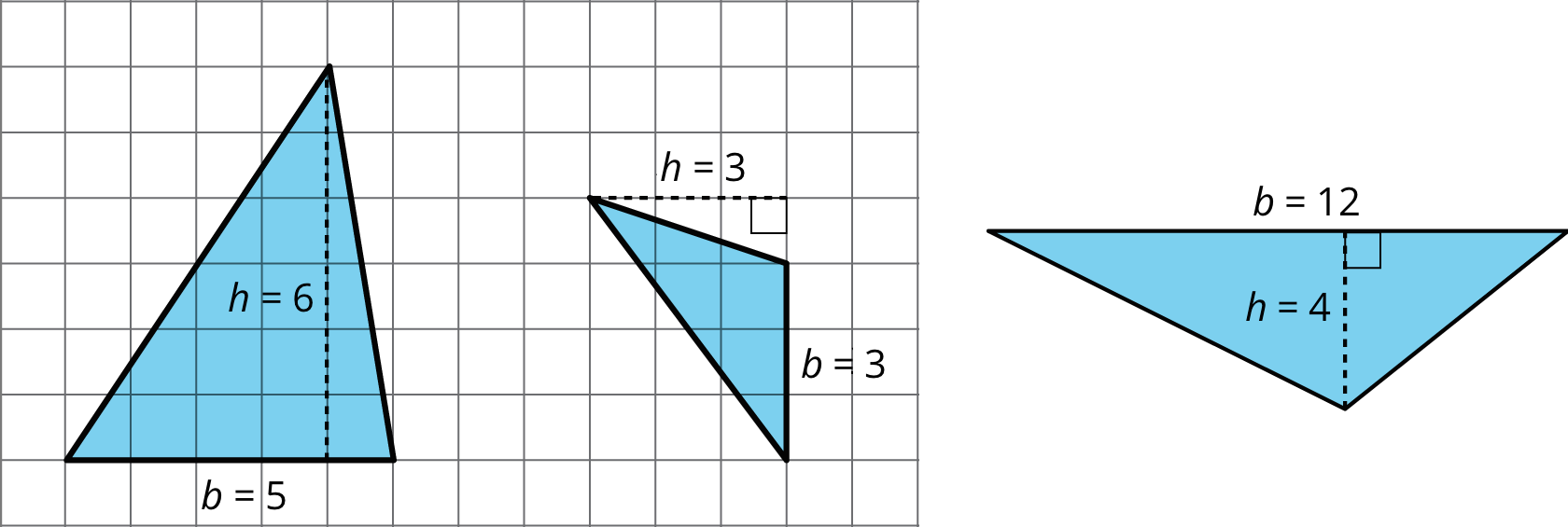
-
The area of Triangle A is 15 square units because \(\frac12 \boldcdot 5 \boldcdot 6=15\).
-
The area of Triangle B is 4.5 square units because \(\frac12 \boldcdot 3 \boldcdot 3 = 4.5\).
-
The area of Triangle C is 24 square units because \(\frac12 \boldcdot 12 \boldcdot 4 = 24\).
In each case, one side of the triangle is the base but neither of the other sides is the height. This is because the angle between them is not a right angle.
In right triangles, however, the two sides that are perpendicular can be a base and a height.
The area of this triangle is 18 square units whether we use 4 units or 9 units for the base.