Lesson 12
What is Surface Area?
12.1: Covering the Cabinet (Part 1) (5 minutes)
Warm-up
This activity prepares students to think about surface area, which they explore in this lesson and upcoming lessons. Students watch a video of a cabinet being gradually tiled with non-overlapping sticky notes. The cabinet was left only partially tiled, which raises the question of the number of sticky notes it takes to cover the entire rectangular prism. Students estimate the answer to this question.
This activity was inspired by Andrew Stadel. Media used with permission. http://www.estimation180.com/filecabinet.
Launch
Arrange students in groups of 2. Show the video of a teacher beginning to cover a large cabinet with sticky notes or display the following still images for all to see. Before starting the video or displaying the image, ask students be prepared to share one thing they notice and one thing they wonder.

Give students a minute to share their observation and question with a partner. Invite a few students to share their questions with the class. If the question “How many sticky notes would it take to cover the entire cabinet?” is not mentioned, ask if anyone wondered how many sticky notes it would take to cover the entire cabinet.
Give students a minute to make an estimate.
Student Facing
Your teacher will show you a video about a cabinet or some pictures of it.
Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Poll the class for students' estimates, and record them for all to see. Invite a couple of students to share how they made their estimate. Explain to students that they will now think about how to answer this question.
12.2: Covering the Cabinet (Part 2) (20 minutes)
Activity
After making an estimate of the number of sticky notes on a cabinet in the warm-up, students now brainstorm ways to find that number more accurately and then go about calculating an answer. The activity prompts students to transfer their understandings of the area of polygons to find the surface area of a three-dimensional object.
Students learn that the surface area of a three-dimensional figure is the total area of all its faces. Since the area of a region is the number of square units it takes to cover the region without gaps and overlaps, surface area can be thought of as the number of square units that needed to cover all sides of an object without gaps and overlaps. The square sticky notes illustrate this idea in a concrete way.
As students work, notice the varying approaches taken to determine the number of sticky notes needed to tile the faces of the cabinet (excluding the bottom). Identify students with different strategies to share later.
Launch
Arrange students in groups of 2–4. Give students 1 minute of quiet time to think about the first question and another minute to share their responses with their group. Ask students to pause afterwards.
Select some students to share how they might go about finding out the number of sticky notes and what information they would need. Students may ask for some measurements:
- The measurements of the cabinet in terms of sticky notes: Tell students that the cabinet is 24 by 12 by 6.
- The measurements of the cabinet in inches or centimeters: Tell students that you don’t have that information and prompt them to think of another piece of information they could use.
- The measurements of each sticky note: Share that it is 3 inches by 3 inches.
If no students mention needing the edge measurements of the cabinet in terms of sticky notes, let them begin working on the second question and provide the information when they realize that it is needed. Give students 8–10 minutes for the second question.
Student Facing
Earlier, you learned about a cabinet being covered with sticky notes.
- How could you find the actual number of sticky notes it will take to cover the cabinet, excluding the bottom? What information would you need to know?
- Use the information you have to find the number of sticky notes to cover the cabinet. Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
How many sticky notes are needed to cover the outside of 2 cabinets pushed together (including the bottom)? What about 3 cabinets? 20 cabinets?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may treat all sides as if they were congruent rectangles. That is, they find the area of the front of the cabinet and then just multiply by 5, or act as if the top is the only side that is not congruent to the others. If there is a real cabinet (or any other large object in the shape of a rectangular prism) in the classroom, consider showing students that only the sides opposite each other can be presumed to be identical.
Students may neglect the fact that the bottom of the cabinet will not be covered. Point out that the bottom is inaccessible because of the floor.
Activity Synthesis
Invite previously identified students or groups to share their answer and strategy. On a visual display, record each answer and each distinct process for determining the surface area (i.e. multiplying the side lengths of each rectangular face and adding up the products). After each presentation, poll the class on whether others had the same answer or process.
Play the video that reveals the actual number of sticky notes needed to cover the cabinet. If students' answers vary from that shown on the video, discuss possible reasons for the differences. (For example, students may not have accounted for the cabinet's door handles. Some may have made a calculation error.)
Tell students that the question they have been trying to answer is one about the surface area of the cabinet. Explain that the surface area of a three-dimensional figure is the total area of all its surfaces. We call the flat surfaces on a three-dimensional figure its faces.
The surface area of a rectangular prism would then be the combined area of all six of its faces. In the context of this problem, we excluded the bottom face, since it is sitting on the ground and will not be tiled with sticky notes. Discuss:
- “What unit of measurement are we using to represent the surface area of the cabinet?” (Square sticky notes)
- “Would the surface area change if we used larger or smaller sticky notes? How?” (Yes, if we use larger sticky notes, we would need fewer. If we use smaller ones, we would need more.)
Design Principles(s): Cultivate conversation; Maximize meta-awareness
12.3: Building with Snap Cubes (20 minutes)
Activity
This activity encourages students to apply strategies for finding the area of polygons to finding the surface area of rectangular prisms. Students use 12 cubes to build a prism, think about its surface area, and use isometric dot paper to draw their prism.
As students build their prisms, notice those with different designs and those with the same design but different approaches to finding surface area (e.g. by counting individual square, by multiplying the edge lengths of rectangular faces, etc.).
Launch
Read the first two lines of the task statement together. Remind students that we refer to the flat surfaces of a three-dimensional figure as faces.
Give students a minute to think about how we know the surface area of the shown prism is 32 square units. Ask 1–2 students to explain their reasoning to the class. Use students’ explanations to highlight the meaning of surface area, i.e., that the area of all the faces need to be accounted for, including those we cannot see when looking at a two-dimensional drawing.
Tell students they will use 12 cubes to build a different prism, draw it, and find its surface area. Consider doing a quick demonstration on how to draw a simple prism on isometric dot paper. (Start with one cube and then add a cube in each dimension.) Tell students that in this activity, we call each face of a single cube, "1 square unit."
Give each student 12 cubes to build a prism and 6–8 minutes of quiet work time. If students are using snap cubes, say that we will pretend all of the faces are completely smooth, so they do not need to worry about the “innies and outies” of the snap cubes.
As students work, consider arranging two students with contrasting designs or strategies as partners. Ask partners to share their answers, explanations, and drawings. Stress that each partner should focus their explanation on how they went about finding surface area. The listener should think about whether the explanation makes sense or if anything is amiss in the reasoning.
For students in digital classrooms, an applet can be used to build and draw prisms. Physical cubes are still recommended and preferred for the building of the figures, however.
Supports accessibility for: Visual-spatial processing; Conceptual processing; Fine-motor skills
Student Facing
Here is a rectangular prism built from 12 cubes:

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units.
The applet has 12 blocks, too. They are all in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. To use a block, drag the red point to move it. Click on the red points to change from left/right movement to up/down movement.
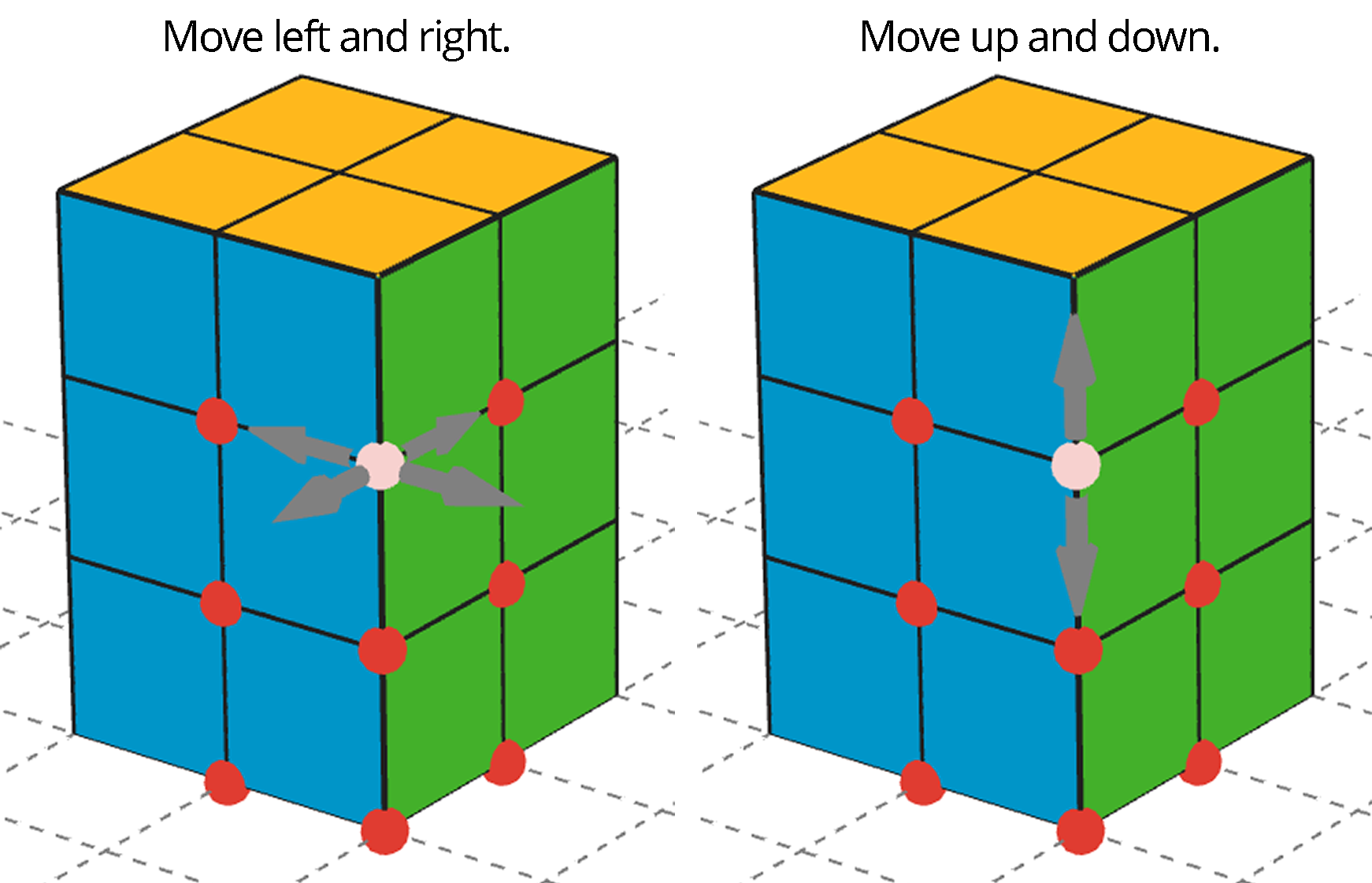
Use all 12 cubes to build a different rectangular prism (with different edge lengths than shown in the prism here). You can turn the view to see all of the faces of your figure.
- How many faces does your figure have?
- What is the surface area of your figure in square units?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Read the first two lines of the task statement together. Remind students that we refer to the flat surfaces of a three-dimensional figure as faces.
Give students a minute to think about how we know the surface area of the shown prism is 32 square units. Ask 1–2 students to explain their reasoning to the class. Use students’ explanations to highlight the meaning of surface area, i.e., that the area of all the faces need to be accounted for, including those we cannot see when looking at a two-dimensional drawing.
Tell students they will use 12 cubes to build a different prism, draw it, and find its surface area. Consider doing a quick demonstration on how to draw a simple prism on isometric dot paper. (Start with one cube and then add a cube in each dimension.) Tell students that in this activity, we call each face of a single cube, "1 square unit."
Give each student 12 cubes to build a prism and 6–8 minutes of quiet work time. If students are using snap cubes, say that we will pretend all of the faces are completely smooth, so they do not need to worry about the “innies and outies” of the snap cubes.
As students work, consider arranging two students with contrasting designs or strategies as partners. Ask partners to share their answers, explanations, and drawings. Stress that each partner should focus their explanation on how they went about finding surface area. The listener should think about whether the explanation makes sense or if anything is amiss in the reasoning.
For students in digital classrooms, an applet can be used to build and draw prisms. Physical cubes are still recommended and preferred for the building of the figures, however.
Supports accessibility for: Visual-spatial processing; Conceptual processing; Fine-motor skills
Student Facing
Here is a sketch of a rectangular prism built from 12 cubes:

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units.
Your teacher will give you 12 snap cubes. Use all of your snap cubes to build a different rectangular prism (with different edge lengths than the prism shown here).
- How many faces does your figure have?
- What is the surface area of your figure in square units?
-
Draw your figure on isometric dot paper. Color each face a different color.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may count the faces of the individual snap cubes rather than faces of the completed prism. Help them understand that the faces are the visible ones on the outside of the figure.
Activity Synthesis
After partner discussions, select a student to highlight for the class the strategy (or strategies) for finding surface area methodically. Point out that in this activity each face of their prism is a rectangle, and that we can find the area of each rectangle by multiplying its side lengths and then add the areas of all the faces.
Explain that later, when we encounter non-rectangular prisms, we can likewise reason about the area of each face the way we reasoned about the area of a polygon.
Design Principle(s): Support sense-making; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, we found the surface areas of a cabinet and of rectangular prisms built out of cubes.
-
"What does it mean to find the surface area of a three-dimensional figure?" (It means finding the number of unit squares that cover the entire surface of the object without gaps or overlaps.)
-
"How can we find the number of unit squares that cover the entire surface of an object?" (We can count them, or we can find the area of each face of the object and add the areas of all faces.)
-
"How are finding surface area and finding area alike? How are they different?" (They both involve finding the number of unit squares that cover a region entirely without gaps and overlaps. Both have to do with two-dimensional regions. Finding area involves a single polygon. Finding surface area means finding the sum of the areas of multiple polygons (faces) of which a three-dimensional figure is composed.)
12.4: Cool-down - A Snap Cube Prism (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
- The surface area of a figure (in square units) is the number of unit squares it takes to cover the entire surface without gaps or overlaps.
- If a three-dimensional figure has flat sides, the sides are called faces.
- The surface area is the total of the areas of the faces.
For example, a rectangular prism has six faces. The surface area of the prism is the total of the areas of the six rectangular faces.

So the surface area of a rectangular prism that has edge-lengths 2 cm, 3 cm, and 4 cm has a surface area of \(\displaystyle (2\boldcdot 3)+ (2\boldcdot 3) + (2\boldcdot 4) + (2\boldcdot 4) + (3\boldcdot 4) + (3\boldcdot 4)\) or 52 square centimeters.