Lesson 18
Surface Area of a Cube
18.1: Exponent Review (5 minutes)
Warm-up
In this warm-up, students compare pairs of numerical expressions and identify the expression with the greater value. The task allows students to review what they learned about exponents and prompts them to look for and make use of structure in numerical expressions (MP7).
Students should do these without calculators and without calculating, although it is fine for them to check their answers with a calculator.
Launch
Give students 1–2 minutes of quiet think time. Ask them to answer the questions without multiplying anything or using a calculator, and to give a signal when they have an answer for each question and can explain their reasoning.
Student Facing
Select the greater expression of each pair without calculating the value of each expression. Be prepared to explain your choices.
- \(10 \boldcdot 3\) or \(10^3\)
- \(13^2\) or \(12 \boldcdot 12\)
- \(97+97+97+97+97+97\) or \(5 \boldcdot 97\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
When given an expression with an exponent, students may misinterpret the base and the exponent as factors and multiply the two numbers. Remind them about the meaning of the exponent notation. For example, show that \(5 \boldcdot 3\) = 15, which is much smaller than \(5 \boldcdot 5 \boldcdot 5\), which equals 125.
Activity Synthesis
Ask one or more students to explain their reasoning for each choice. If not mentioned in students’ explanations, highlight the structures in the expressions that enable us to evaluate each one without performing any calculations.
Point out, for example, that since we know that \(10^3\) means \(10 \boldcdot 10 \boldcdot 10\), we can tell that it is much larger than \(10 \boldcdot 3\).
For the last question, remind students that we can think of repeated addition in terms of multiple groups (i.e., that the sum of six 97s can be seen as six groups of 97 or \(6 \boldcdot 97\)). The idea of using groups to write equivalent expressions will support students as they write expressions for the surface area of a cube later in the lesson (i.e., writing the areas of all square faces of a cube as \(6s^2\)) .
18.2: The Net of a Cube (20 minutes)
Activity
This activity contains two sets of problems. The first set involves computations with simple numbers and should be solved numerically. Use students’ work here to check that they are drawing a net correctly.
The second set encourages students to write expressions rather than to simplify them through calculations. The goal is to prepare students for the general rules \(s^3\) and \(6s^2\), which are more easily understood through an intermediate step involving numbers.
Note that students will be introduced to the idea that \(5 \boldcdot x\) means the same as \(5x\) in a later unit, so expect them to write \(6 \boldcdot 17^2\) instead of \(6 (17^2)\). It is not critical that they understand that a number and a variable (or a number and an expression in parentheses) placed next to each other means they are being multiplied.
As students work on the second set, monitor the ways in which they write their expressions for surface area and volume. Identify those whose expressions include :
- products (e.g., \(17 \boldcdot 17\) or \(17 \boldcdot 17 \boldcdot 17\)),
- sums of products (e.g., \((17 \boldcdot 17)+(17 \boldcdot 17)+…\)),
- combination of like terms (e.g., \(6 \boldcdot(17 \boldcdot 17)\)),
- exponents (e.g., \(17^2 + 17^2 +…\)) or \(17^3\)), and
- completed calculation (e.g., \(289\)).
Select these students to share their work later. Notice the lengths of the expressions and sequence their explanations in order—from the longest expression to the most succinct.
Launch
Arrange students in groups of 2. Give students access to their geometry toolkits and 8-10 minutes of quiet work time. Tell students to try to answer the questions without using a calculator. Ask them to share their responses with their partner afterwards.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
-
A cube has edge length 5 inches.
-
Draw a net for this cube, and label its sides with measurements.
- What is the shape of each face?
- What is the area of each face?
- What is the surface area of this cube?
- What is the volume of this cube?
-
-
A second cube has edge length 17 units.
-
Draw a net for this cube, and label its sides with measurements.
- Explain why the area of each face of this cube is \(17^2\) square units.
- Write an expression for the surface area, in square units.
- Write an expression for the volume, in cubic units.
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might think the surface area is \((17 \boldcdot 17)^6\). Prompt students to write down how they would compute surface area step by step, before trying to encapsulate their steps in an expression. Dissuade students from using calculators in the last two problems and assure them that building an expression does not require extensive computation.
Students may think that refraining from using a calculator meant performing all calculations—including those of larger numbers—on paper or mentally, especially if they are unclear about the meaning of the term “expression.” Ask them to refer to the expressions in the warm-up, or share examples of expressions in a few different forms, to help them see how surface area and volume can be expressed without computation.
Activity Synthesis
After partner discussions, select a couple of students to present the solutions to the first set of questions, which should be straightforward.
Then, invite previously identified students to share their expressions for the last two questions. If possible, sequence their presentation in the following order. If any expressions are missing but needed to illustrate the idea of writing succinct expressions, add them to the lists.
Surface area:
- \((17 \boldcdot 17)+(17 \boldcdot 17)+(17 \boldcdot 17)+(17 \boldcdot 17)+(17 \boldcdot 17)+(17 \boldcdot 17)\)
- \(17^2+17^2+17^2+17^2+17^2+17^2\)
- \(6 \boldcdot(17 \boldcdot 17)\)
- \(6 \boldcdot (17^2)\)
- \(6 \boldcdot (289)\)
- 1,734
Volume:
- \(17 \boldcdot 17 \boldcdot 17\)
- \(17^3\)
- 4,913
Discuss how multiplication can simplify expressions involving repeated addition and exponents can do the same for repeated multiplication. While the last expression in each set above is the simplest to write, getting there requires quite a bit of computation. Highlight \(6\boldcdot 17^2\) and \(17^3\) as efficient ways to express the surface area and volume of the cube.
As the class discusses the different expressions, consider directing students’ attention to the units of measurements. Remind students that, rather than writing \(6 \boldcdot (17^2)\) square units, we can write \(6 \boldcdot (17^2)\) units2, and instead of \(17^3\) cubic units, we can write \(17^3\) units2. Unit notations will appear again later in the course, so it can also be reinforced later.
If students are not yet ready for the general formula, which comes next, offer another example. For instance, say: “A cube has edge length 38 cm. How can we express its surface area and volume?”
Help students see that its surface area is \(6 \boldcdot (38^2)\) cm2 and its volume is \(38^3\) cm3. The large number will discourage calculation and focus students on the form of the expressions they are building and the use of exponents.
Design Principle(s): Optimize output; Cultivate conversation
18.3: Every Cube in the Whole World (10 minutes)
Activity
In this activity, students build on what they learned earlier and develop the formulas for the surface area and the volume of a cube in terms of a variable edge length \(s\).
Encourage students to refer to their work in the preceding activity as much as possible and to generalize from it. As before, monitor for different ways of writing expressions for surface area and volume. Identify students whose work includes the following:
- products (e.g., \(s \boldcdot s\), or \(s \boldcdot s \boldcdot s\)),
- sums of products (e.g., \((s \boldcdot s)+(s \boldcdot s)+…\)),
- combination of like terms (e.g., \(6 \boldcdot(s \boldcdot s)\)), and
- exponents (e.g., \(s^2 + s^2 +…\), or \(s^3\)).
Select these students to share their work later. Again, notice the lengths of the expressions and sequence their explanations in order—from the longest expression to the most succinct.
Launch
Give students access to their geometry toolkits and 7–8 minutes of quiet think time. Tell students they will be answering on the same questions as before, but with a variable for the side length. Encourage them to use the work they did earlier to help them here.
Student Facing
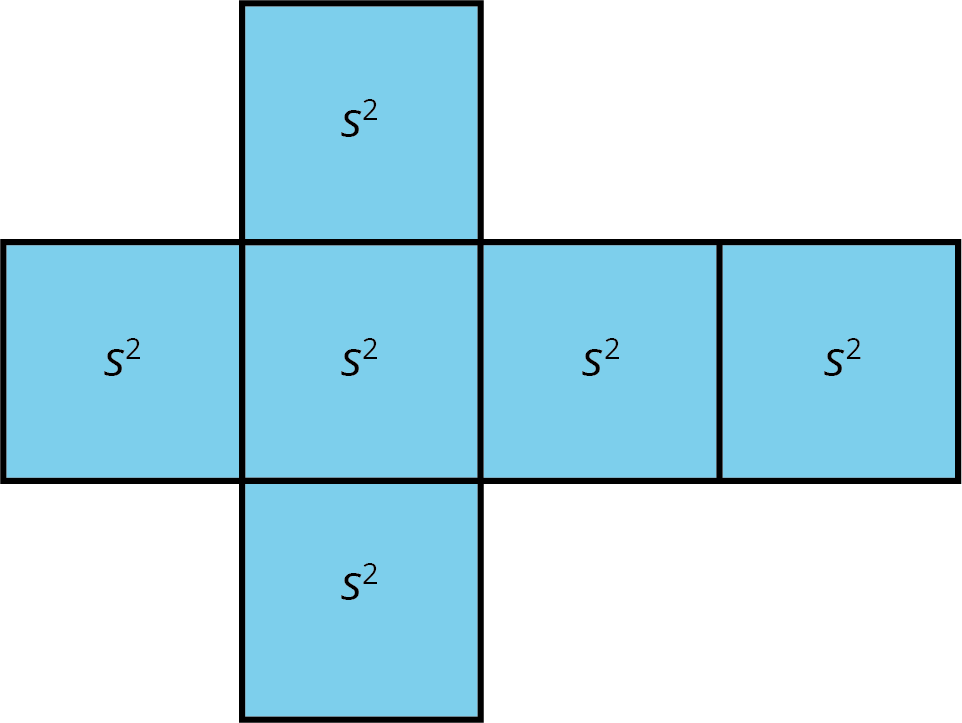
A cube has edge length \(s\).
- Draw a net for the cube.
- Write an expression for the area of each face. Label each face with its area.
- Write an expression for the surface area.
- Write an expression for the volume.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students are unclear or unsure about using the variable \(s\), explain that we are looking for an expression that would work for any edge length, and that a variable, such as \(s\), can represent any number. The \(s\) could be replaced with any edge length in finding surface area and volume.
To connect students’ work to earlier examples, point to the cube with edge length 17 units from the previous activity. Ask: “If you wrote the surface area as \(6 \boldcdot 17^2\) before, what should it be now?”
As students work, encourage those who may be more comfortable using multiplication symbols to instead use exponents whenever possible.
Activity Synthesis
Discuss the problems in as similar a fashion as was done in the earlier activity involving a cube with edge length 17 units. Doing so enables students to see structure in the expressions (MP7) and to generalize through repeated reasoning (MP8).
Select previously identified students to share their responses with the class. If possible, sequence their presentation in the following order to help students see how the expressions \(6 \boldcdot s^2\) and \(s^3\) come about. If any expressions are missing but needed to illustrate the idea of writing succinct expressions, add them to the lists.
Surface area:
- \((s \boldcdot s)+(s \boldcdot s)+(s \boldcdot s)+(s \boldcdot s)+(s \boldcdot s)+(s \boldcdot s)\)
- \(s^2+s^2+s^2+s^2+s^2+s^2\)
- \(6(s \boldcdot s)\)
- \(6 \boldcdot (s^2)\) or \(6 \boldcdot s^2\)
Volume
- \(s \boldcdot s \boldcdot s\)
- \(s^3\)
Refer back to the example involving numerical side length (a cube with edge length 17 units) if students have trouble understanding where the most concise expression of surface area comes from.
Present the surface area as \(6 \boldcdot s^2\). You can choose to also write it as \(6s^2\).
Lesson Synthesis
Lesson Synthesis
Review the formulas for volume and surface area of a cube.
- The volume of a cube with edge length \(s\) is \(s^3\).
- A cube has 6 faces that are all identical squares. The surface area of a cube with edge length \(s\) is \(6 \boldcdot s^2\).
18.4: Cool-down - From Volume to Surface Area (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The volume of a cube with edge length \(s\) is \(s^3\).
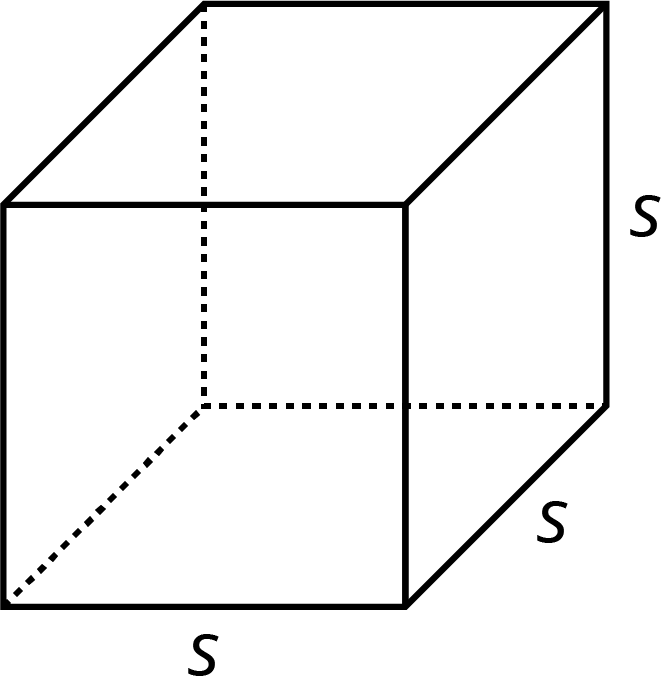
A cube has 6 faces that are all identical squares. The surface area of a cube with edge length \(s\) is \(6 \boldcdot s^2\).