Lesson 15
More Nets, More Surface Area
Let’s draw nets and find the surface area of polyhedra.
15.1: Notice and Wonder: Wrapping Paper
Kiran is wrapping this box of sports cards as a present for a friend.
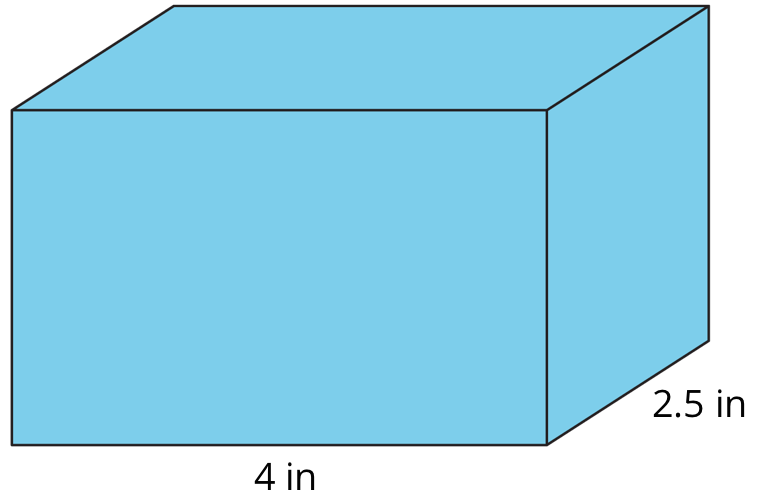
What do you notice? What do you wonder?
15.2: Building Prisms and Pyramids
Your teacher will give you a drawing of a polyhedron. You will draw its net and calculate its surface area.
-
What polyhedron do you have?
-
Study your polyhedron. Then, draw its net on graph paper. Use the side length of a grid square as the unit.
-
Label each polygon on the net with a name or number.
-
Find the surface area of your polyhedron. Show your thinking in an organized manner so that it can be followed by others.
15.3: Comparing Boxes
Here are the nets of three cardboard boxes that are all rectangular prisms. The boxes will be packed with 1-centimeter cubes. All lengths are in centimeters.
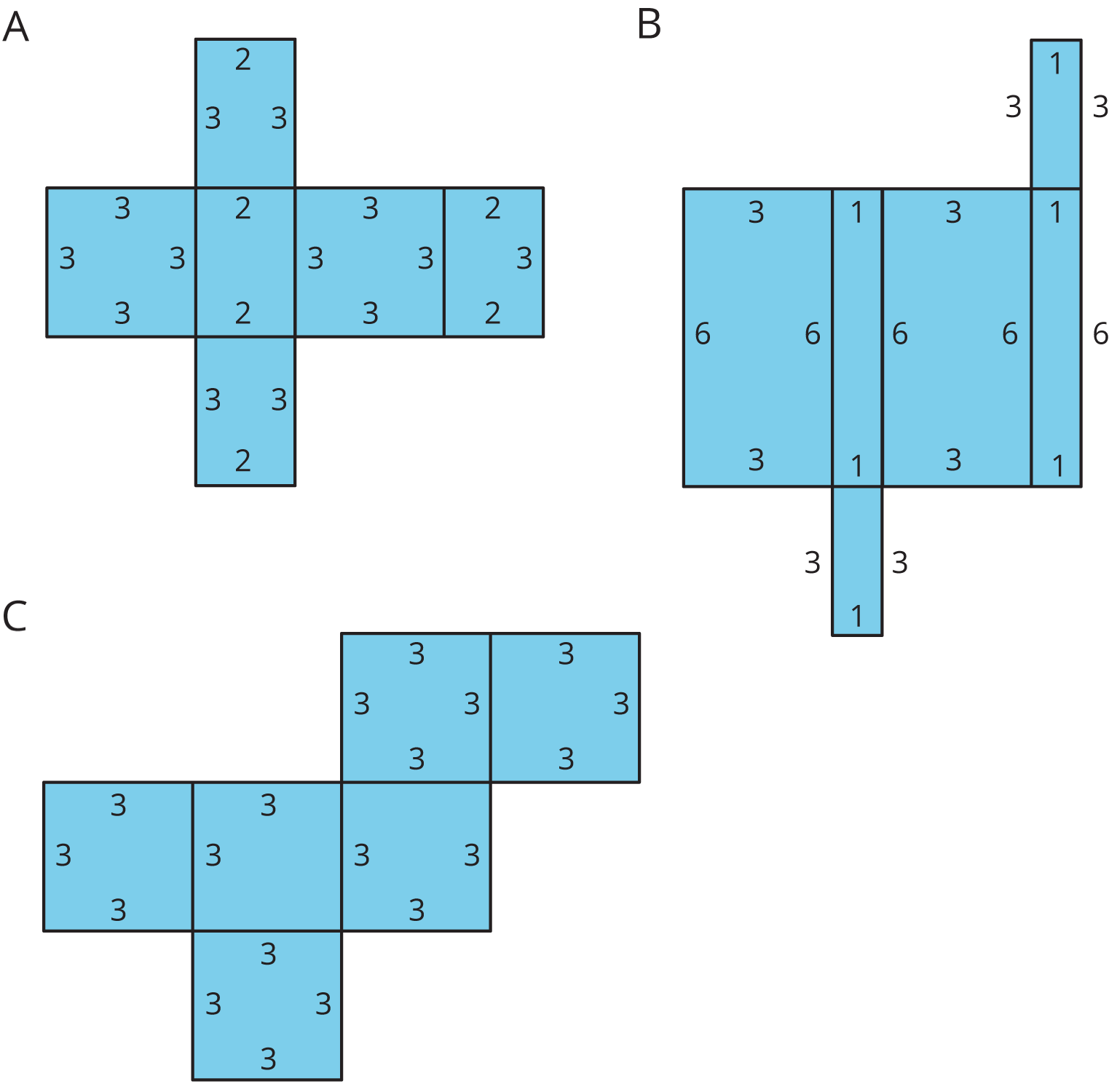
- Compare the surface areas of the boxes. Which box will use the least cardboard? Show your reasoning.
- Now compare the volumes of these boxes in cubic centimeters. Which box will hold the most 1-centimeter cubes? Show your reasoning.
Figure C shows a net of a cube. Draw a different net of a cube. Draw another one. And then another one. How many different nets can be drawn and assembled into a cube?
Summary
The surface area of a polyhedron is the sum of the areas of all of the faces. Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.
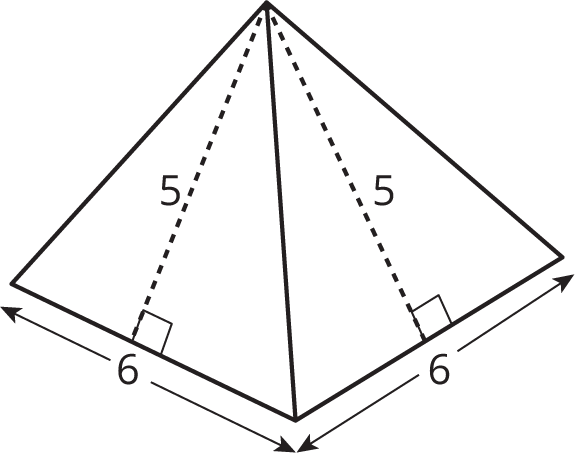
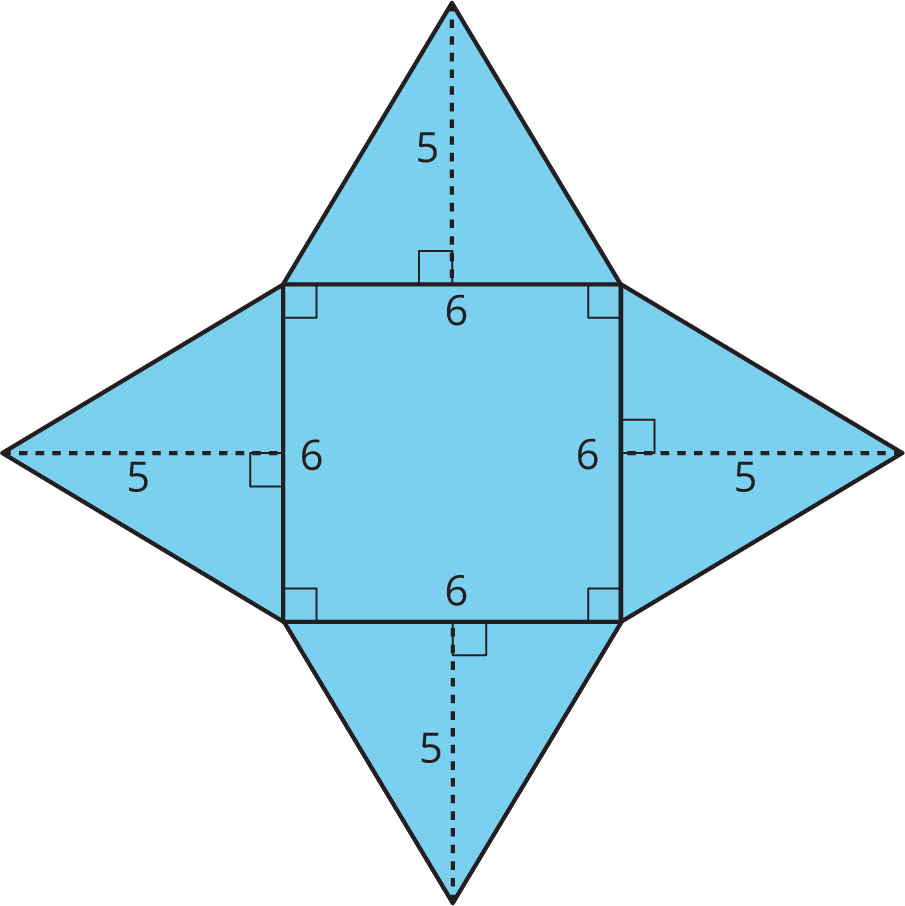
A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces:
\((6\boldcdot 6) + 4\boldcdot \left(\frac12 \boldcdot 5 \boldcdot 6\right) = 96\)
The surface area of this square pyramid is 96 square units.
Video Summary
Glossary Entries
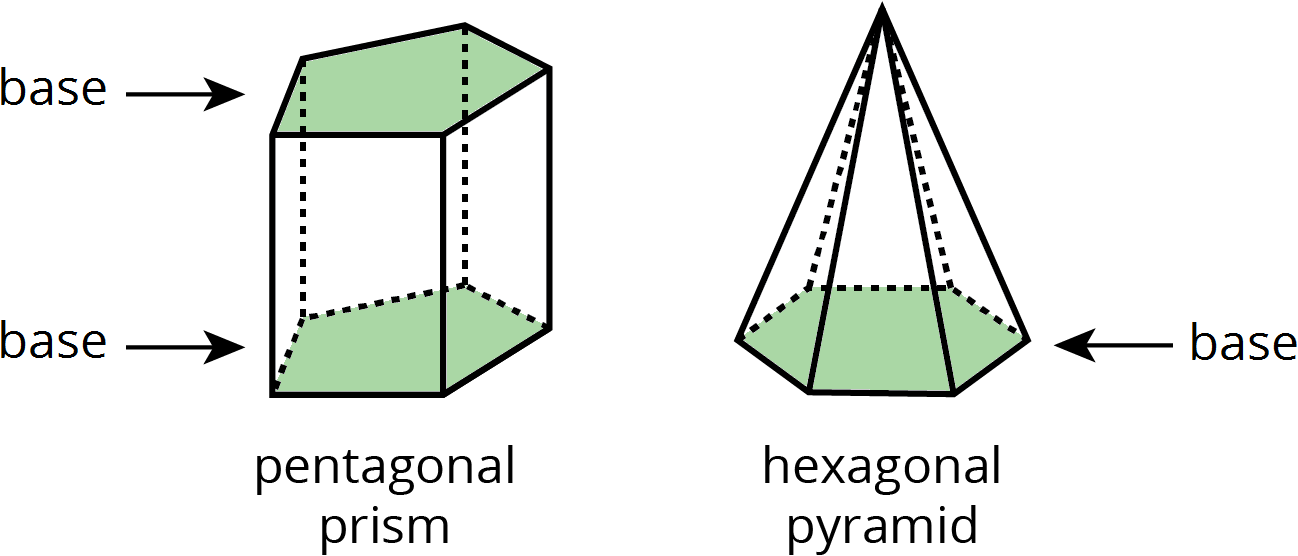
- base (of a prism or pyramid)
The word base can also refer to a face of a polyhedron.
A prism has two identical bases that are parallel. A pyramid has one base.
A prism or pyramid is named for the shape of its base.
- face
Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.
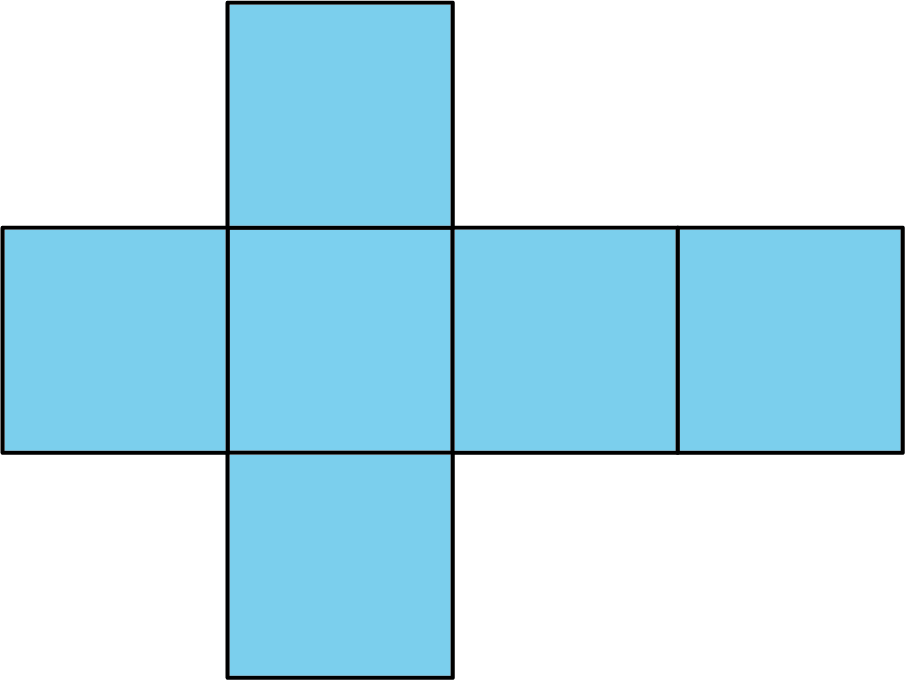
- net
A net is a two-dimensional figure that can be folded to make a polyhedron.
Here is a net for a cube.
- polyhedron
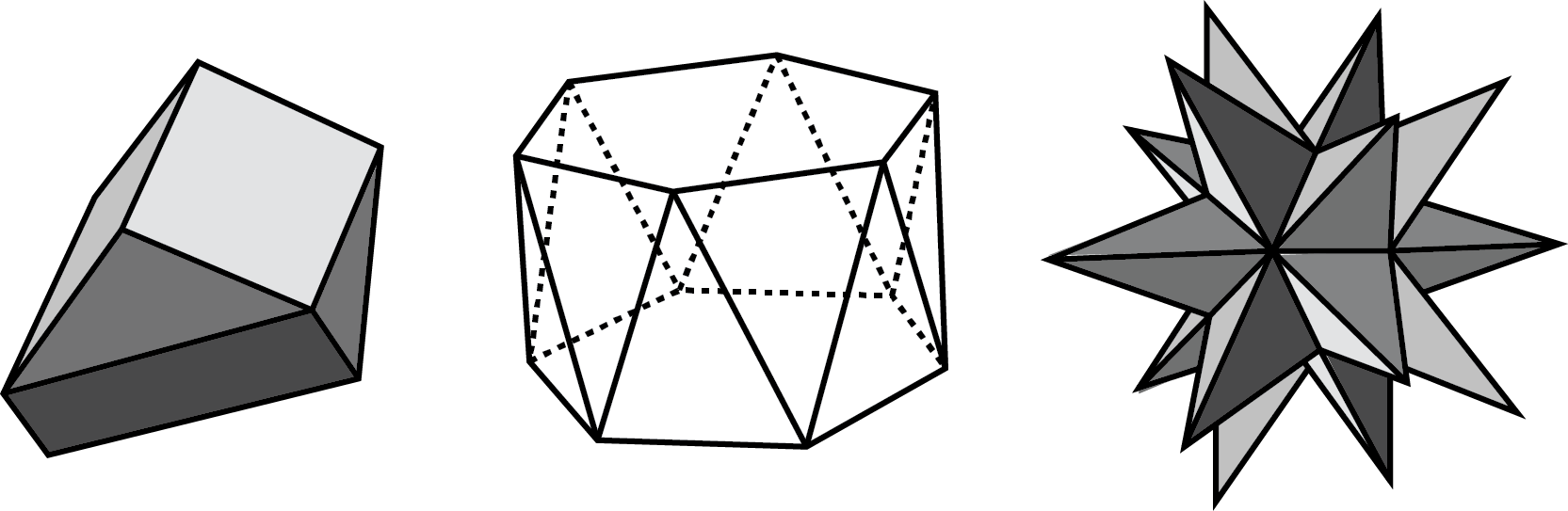
A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.
Here are some drawings of polyhedra.
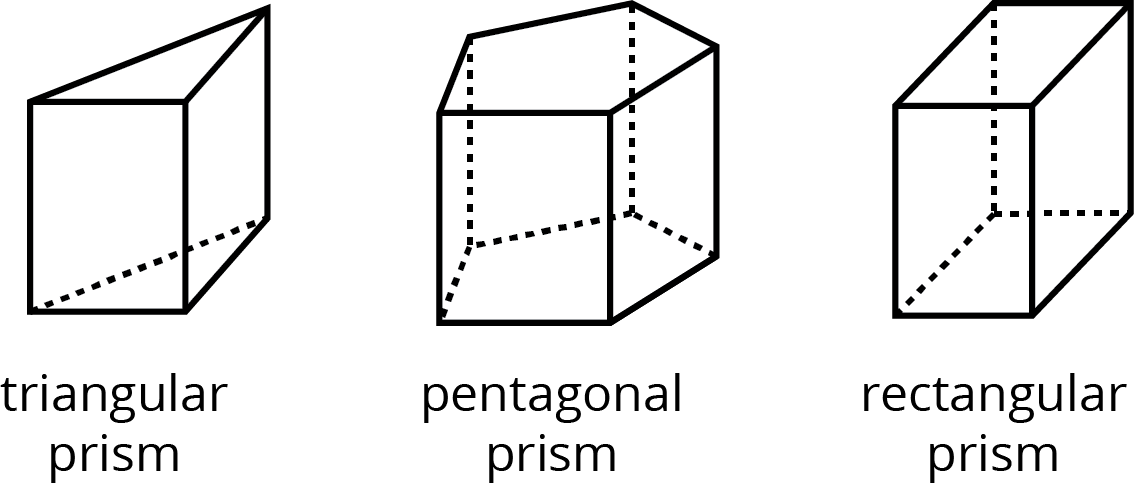
- prism
A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.
Here are some drawings of prisms.
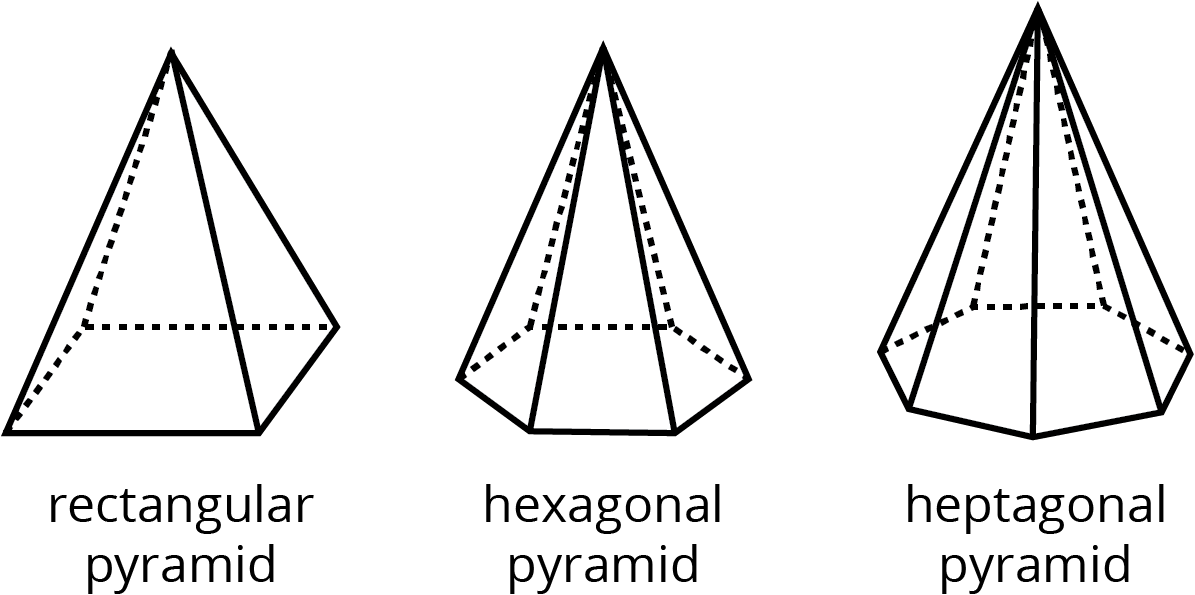
- pyramid
A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.
Here are some drawings of pyramids.
- surface area
The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.
For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is \(6 \boldcdot 9\), or 54 cm2.