Lesson 3
Reasoning to Find Area
Let’s decompose and rearrange shapes to find their areas.
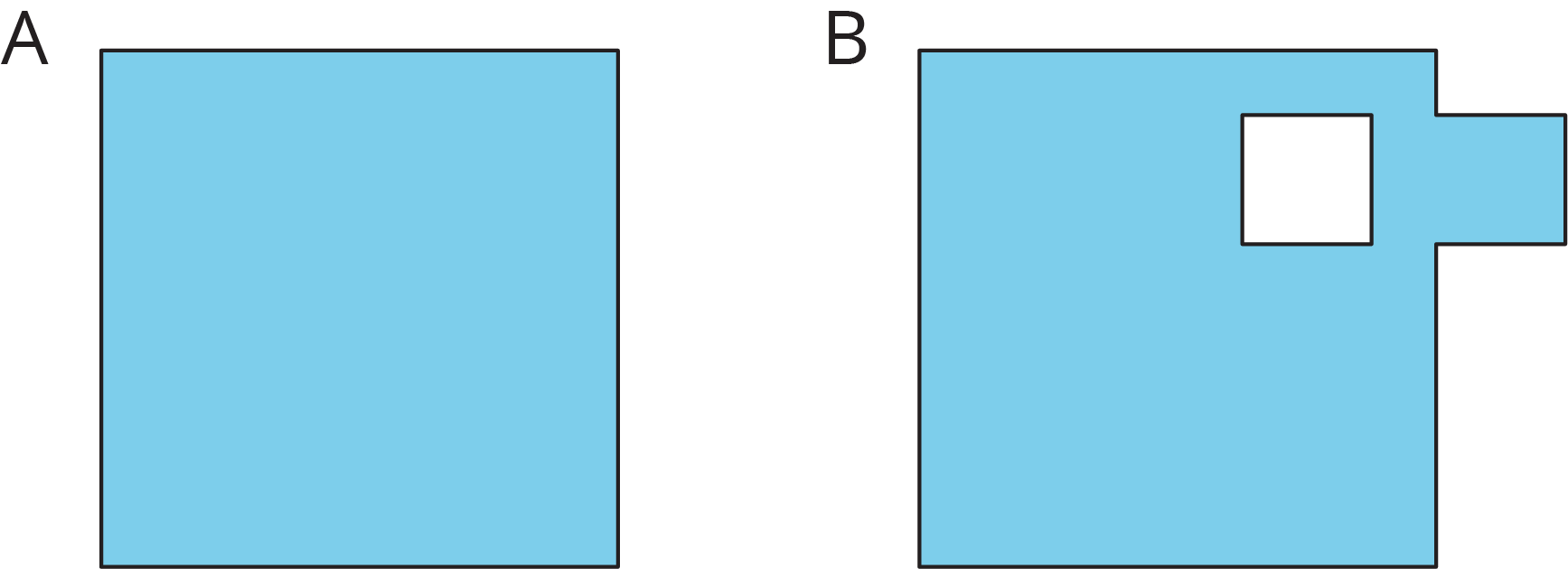
3.1: Comparing Regions
Is the area of Figure A greater than, less than, or equal to the area of the shaded region in Figure B? Be prepared to explain your reasoning.
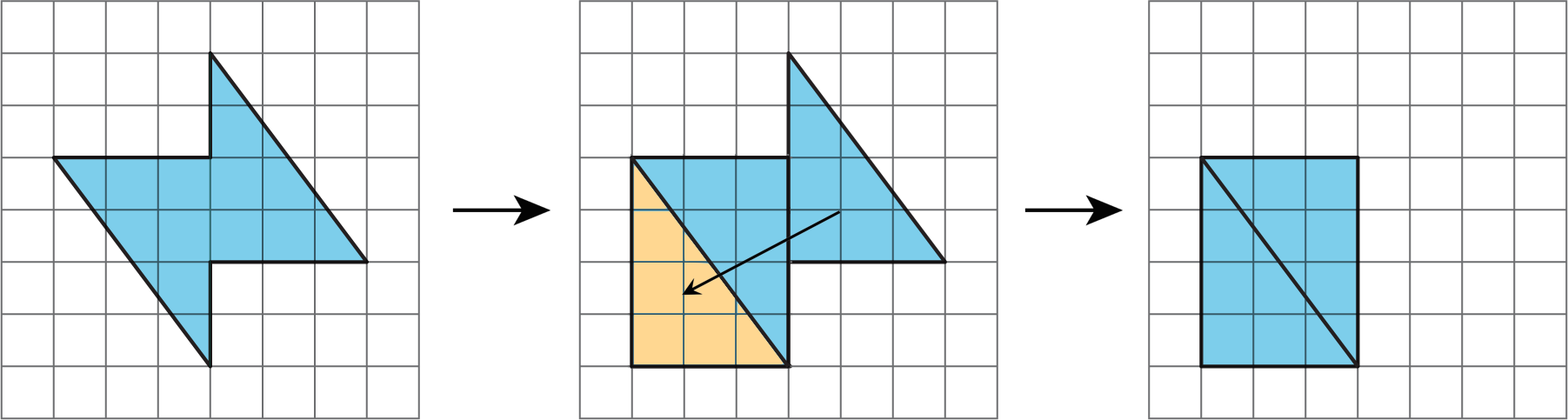
3.2: On the Grid
Each grid square is 1 square unit. Find the area, in square units, of each shaded region without counting every square. Be prepared to explain your reasoning.
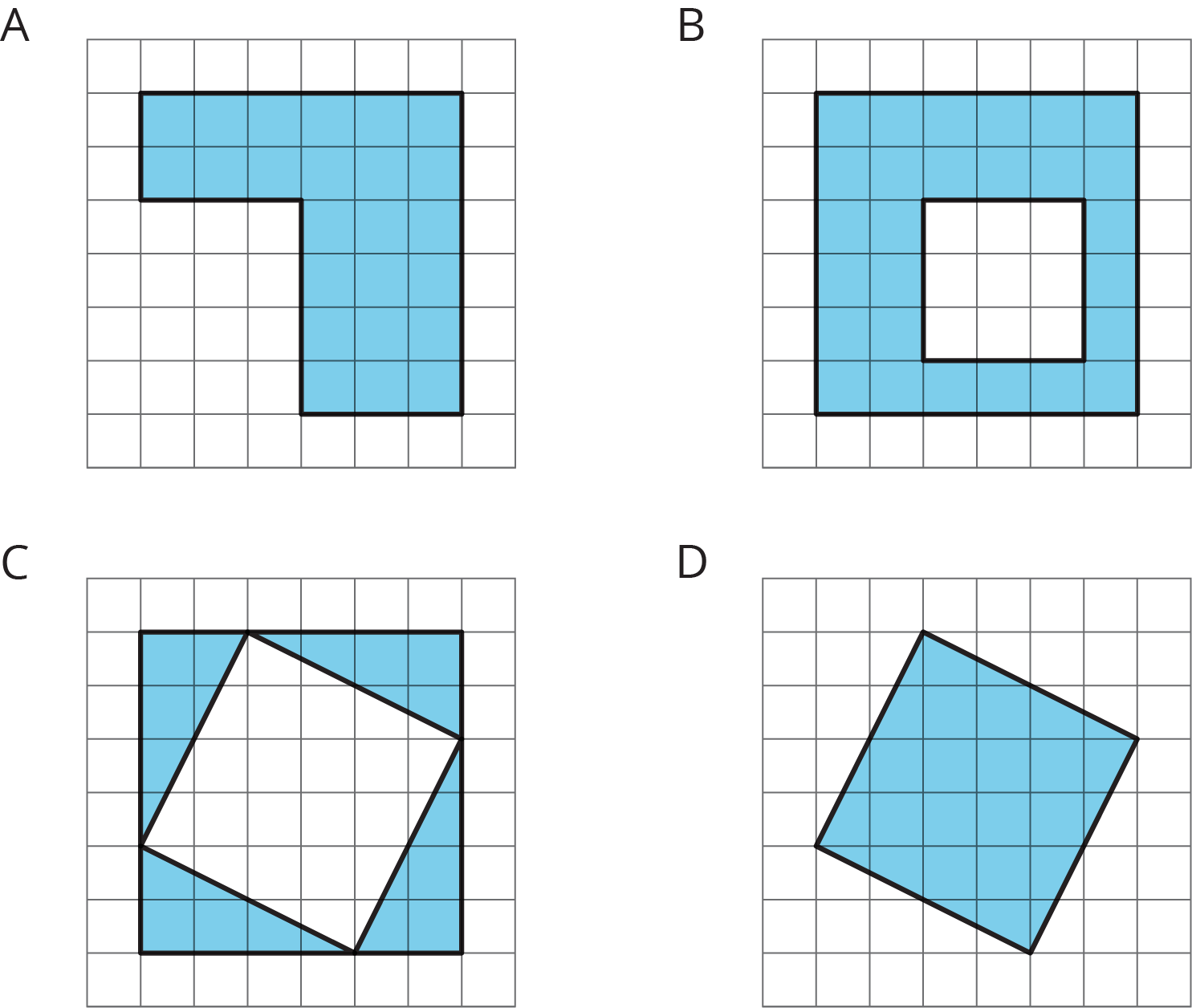
Rearrange the triangles from Figure C so they fit inside Figure D. Draw and color a diagram of your work.
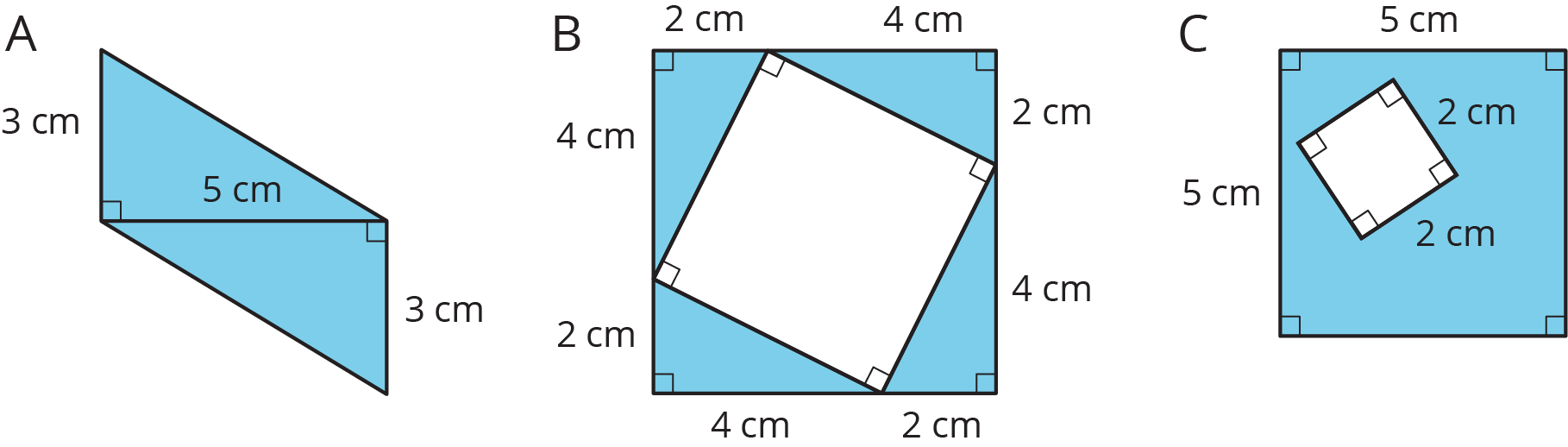
3.3: Off the Grid
Find the area of the shaded region(s) of each figure. Explain or show your reasoning.
Summary
There are different strategies we can use to find the area of a region. We can:
- Decompose it into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.
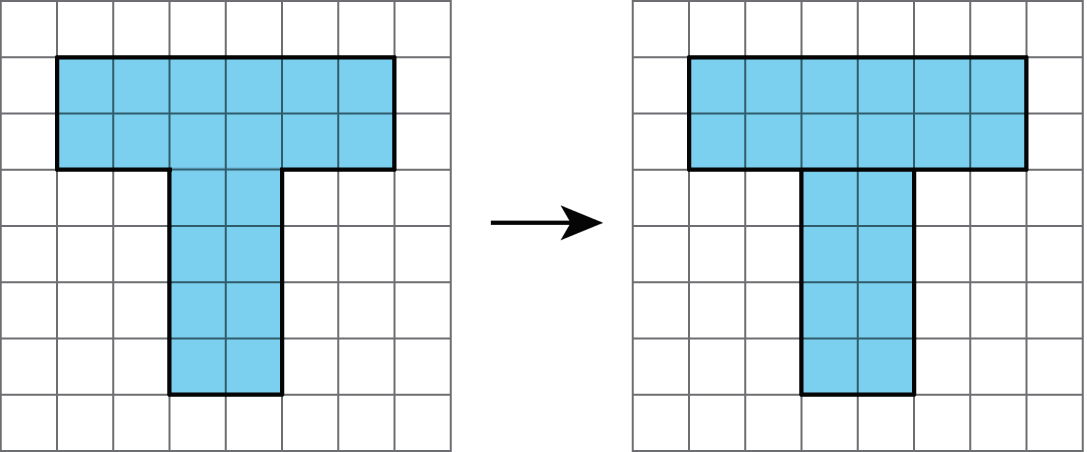
- Decompose it and rearrange the pieces into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.
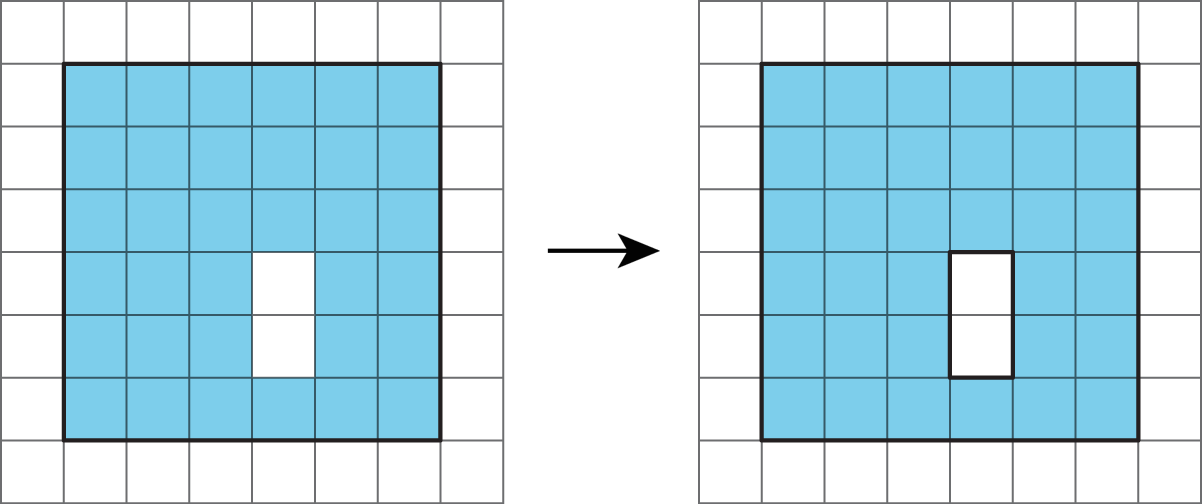
- Consider it as a shape with a missing piece; calculate the area of the shape and the missing piece, and then subtract the area of the piece from the area of the shape.
The area of a figure is always measured in square units. When both side lengths of a rectangle are given in centimeters, then the area is given in square centimeters. For example, the area of this rectangle is 32 square centimeters.

Video Summary
Glossary Entries
- area
Area is the number of square units that cover a two-dimensional region, without any gaps or overlaps.
For example, the area of region A is 8 square units. The area of the shaded region of B is \(\frac12\) square unit.
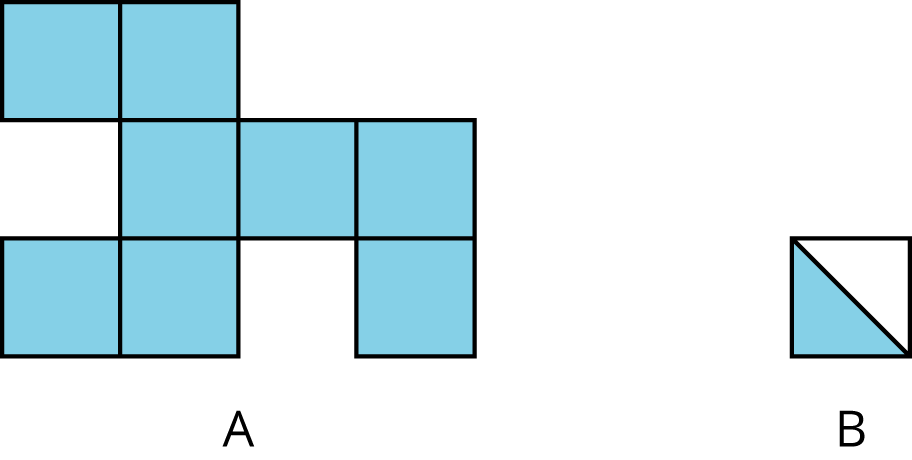
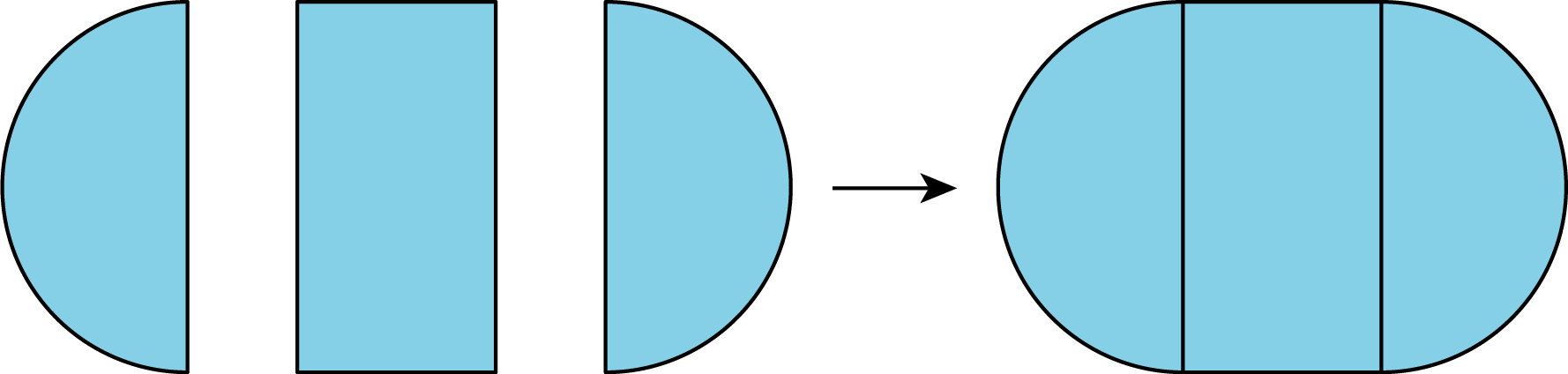
- compose
Compose means “put together.” We use the word compose to describe putting more than one figure together to make a new shape.
- decompose
Decompose means “take apart.” We use the word decompose to describe taking a figure apart to make more than one new shape.

- region
A region is the space inside of a shape. Some examples of two-dimensional regions are inside a circle or inside a polygon. Some examples of three-dimensional regions are the inside of a cube or the inside of a sphere.