Lesson 2
Finding Area by Decomposing and Rearranging
Lesson Narrative
This lesson begins by revisiting the definitions for area that students learned in earlier grades. The goal here is to refine their definitions (MP6) and come up with one that can be used by the class for the rest of the unit. They also learn to reason flexibly about two-dimensional figures to find their areas, and to communicate their reasoning clearly (MP3).
The area of two-dimensional figures can be determined in multiple ways. We can compose that figure using smaller pieces with known areas. We can decompose a figure into shapes whose areas we can determine and add the areas of those shapes. We can also decompose it and rearrange the pieces into a different but familiar shape so that its area can be found. The two key principles in this lesson are:
- Figures that match up exactly have equal areas. If two figures can be placed one on top of the other such that they match up exactly, then they have the same area.
- A figure can be decomposed and its pieces rearranged without changing its area. The sum of the areas of the pieces is equal to the area of the original figure. Likewise, if a figure is composed of non-overlapping pieces, its area is equal to the sum of the areas of the pieces. In other words, area is additive.
Students have used these principles since grade 3, but mainly to decompose squares, rectangles, and their composites (e.g., an L-shape) and rearrange them to form other such figures. In this lesson, they decompose triangles and rearrange them to form figures whose areas they know how to calculate.
A note about “two figures that match up exactly”: In grade 8, students will learn to refer to such figures as congruent and to describe congruence in terms of rigid motions (reflections, rotations, and translations). In these materials, the word congruent is not used in grade 6. A possibility is to use an informal term such as “identical,” so that students can talk about one figure being an “identical copy” of another. What “identical” means, however, might also require clarification (e.g., that it is independent of color and orientation).
Learning Goals
Teacher Facing
- Calculate the area of a region by decomposing it and rearranging the pieces, and explain (orally and in writing) the solution method.
- Recognize and explain (orally) that if two figures can be placed one on top one other so that they match up exactly, they must have the same area.
- Show that area is additive by composing polygons with a given area.
Student Facing
Let’s create shapes and find their areas.
Required Materials
Required Preparation
Prepare 1 set of tangrams that contains 4 small, 1 medium, and 2 large right triangles for every 2 students. Print and cut out the blackline master (printing on card stock is recommended), or use commercially-available tangrams. Note that the tangram pieces used here differs from a standard set in that two additional small triangles are used instead of a parallelogram.
A tangram applet is included for classrooms using the digital materials, but students can also be given the option of using physical tangrams instead of the digital tool.
Make sure students have access to their geometry toolkits, which should include tracing paper, graph paper, colored pencils, scissors, and an index card to use as a straightedge or to mark right angles.
Learning Targets
Student Facing
- I can explain how to find the area of a figure that is composed of other shapes.
- I know how to find the area of a figure by decomposing it and rearranging the parts.
- I know what it means for two figures to have the same area.
CCSS Standards
Glossary Entries
-
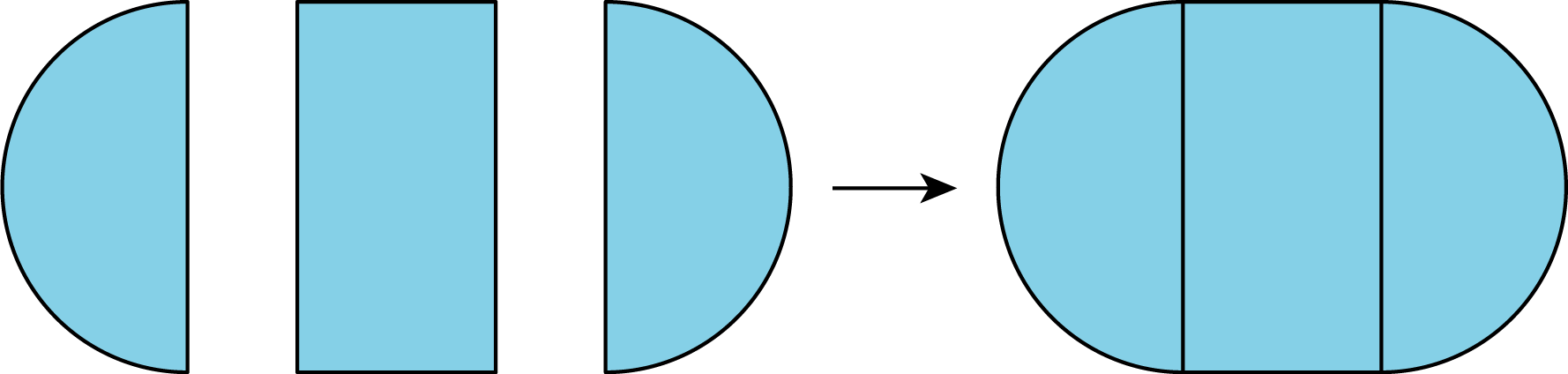
compose
Compose means “put together.” We use the word compose to describe putting more than one figure together to make a new shape.
-
decompose
Decompose means “take apart.” We use the word decompose to describe taking a figure apart to make more than one new shape.

Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |