Lesson 18

Surface Area of a Cube

Let’s write a formula to find the surface area of a cube.

Select the greater expression of each pair without calculating the value of each expression. Be prepared to explain your choices.

A cube has edge length 5 inches.
1. Draw a net for this cube, and label its sides with measurements.
2. What is the shape of each face?
3. What is the area of each face?
4. What is the surface area of this cube?
5. What is the volume of this cube?
A second cube has edge length 17 units.
1. Draw a net for this cube, and label its sides with measurements.
2. Explain why the area of each face of this cube is $17^2$ square units.
3. Write an expression for the surface area, in square units.
4. Write an expression for the volume, in cubic units.

A cube has edge length $s$ .

The volume of a cube with edge length $s$ is $s^3$ .

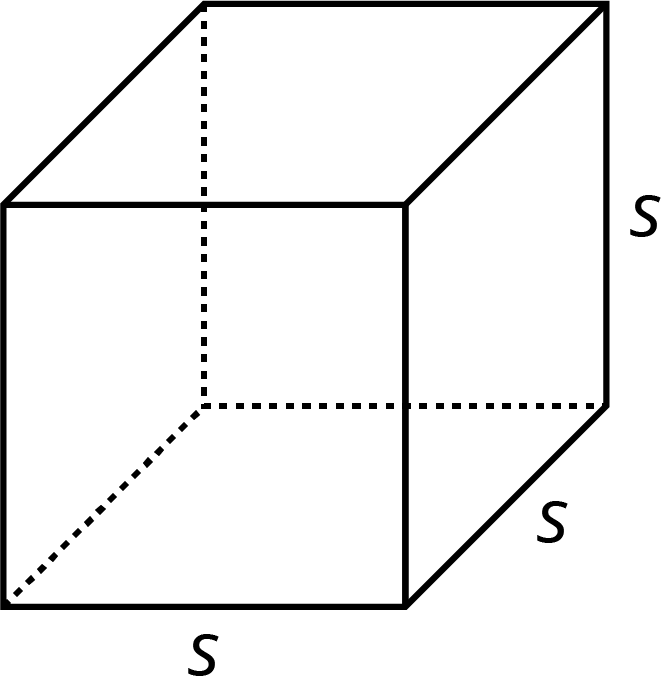
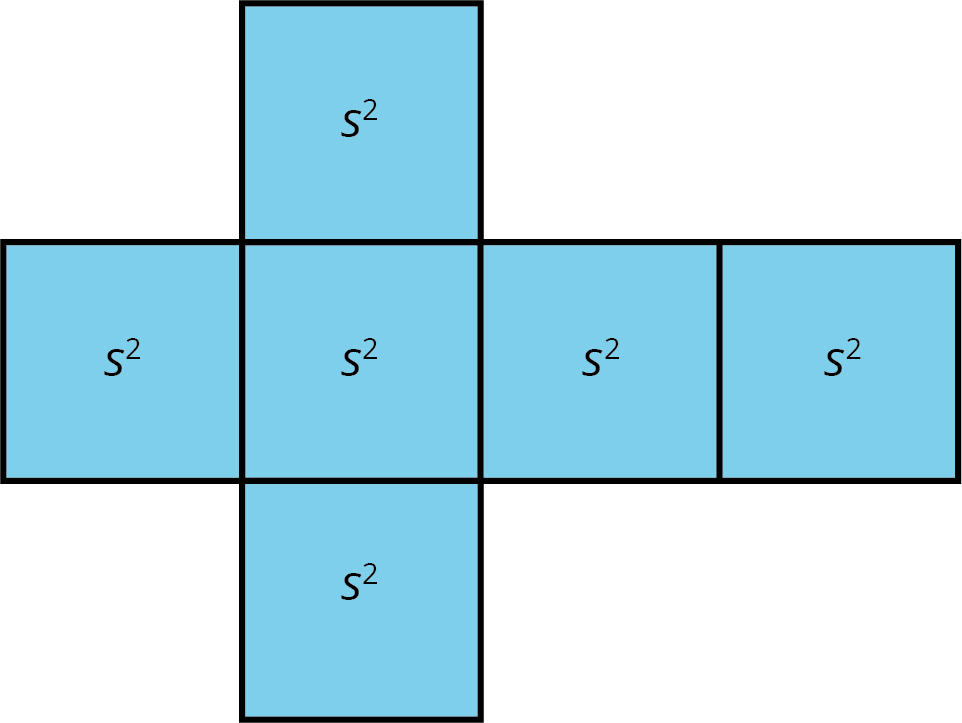
A cube has 6 faces that are all identical squares. The surface area of a cube with edge length $s$ is $6 \boldcdot s^2$ .

Video VLS G6U1V5 Distinguishing between Surface Area and Volume (Lessons 16–18) available at https://player.vimeo.com/video/443563211.

cubed

We use the word cubed to mean “to the third power.” This is because a cube with side length $s$ has a volume of $s \boldcdot s \boldcdot s$ , or $s^3$ .
exponent

In expressions like $5^3$ and $8^2$ , the 3 and the 2 are called exponents. They tell you how many factors to multiply. For example, $5^3$ = $5 \boldcdot 5 \boldcdot 5$ , and $8^2 = 8 \boldcdot 8$ .
squared

We use the word squared to mean “to the second power.” This is because a square with side length $s$ has an area of $s \boldcdot s$ , or $s^2$ .