Lesson 14

Nets and Surface Area

View Student Lesson

Problem 1

Can this net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.

Net of cube 

 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

  1. What polyhedron can be assembled from this net? Explain how you know.

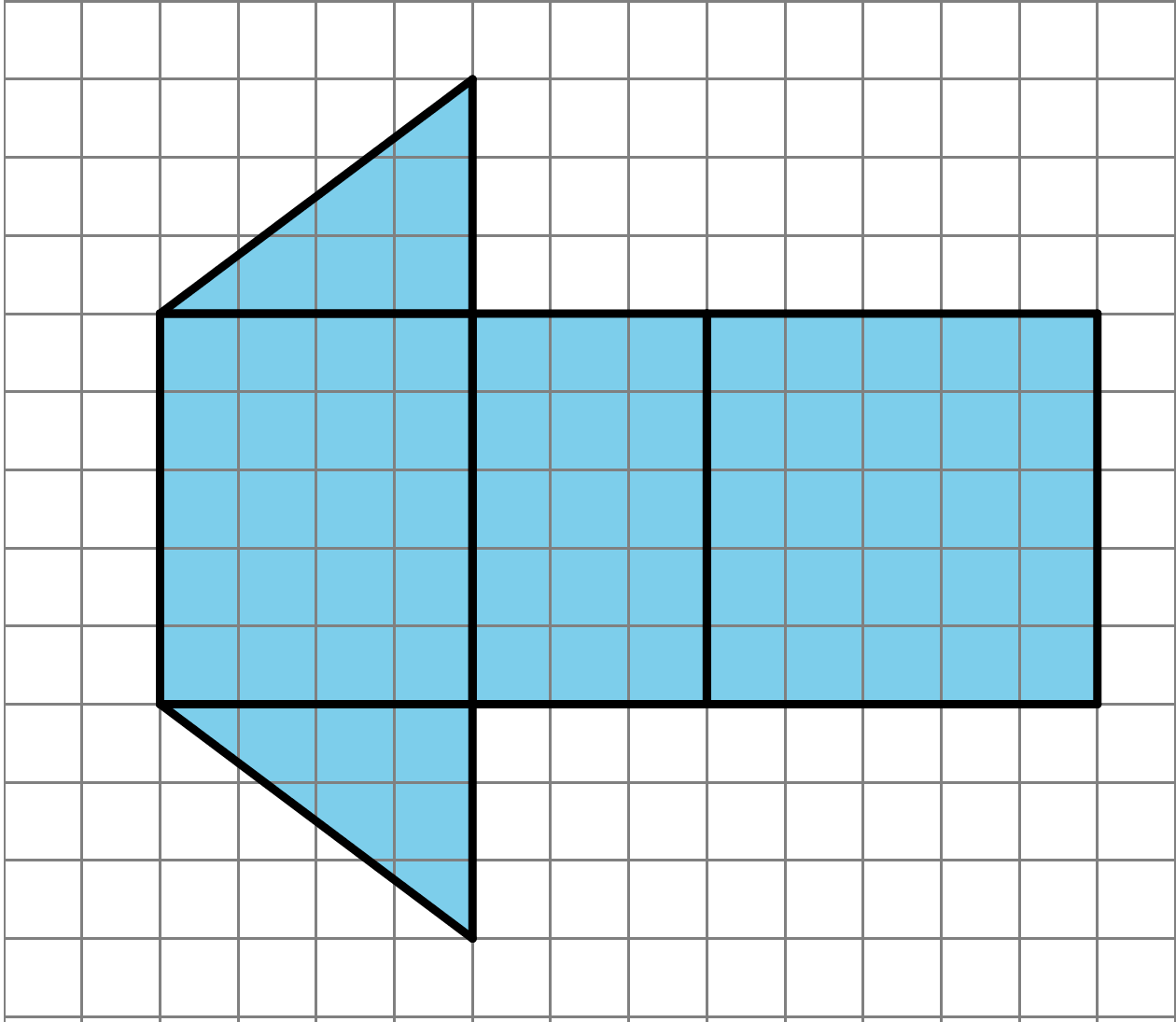
    net on a grid. 

  2. Find the surface area of this polyhedron. Show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.

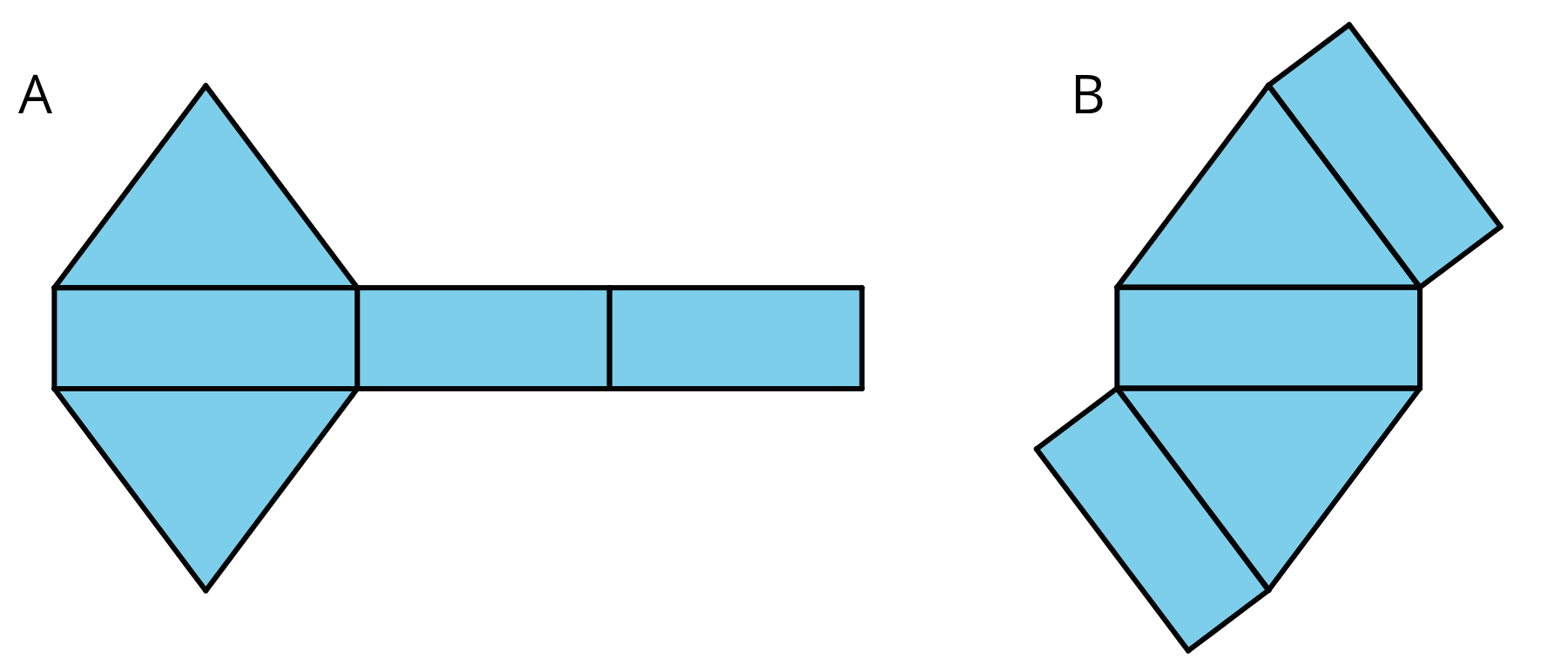
2 nets labeled A and B. A is composed of 2 triangular and 3 rectangular faces. B is composed of the same faces, but they are arranged differently.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Here are two three-dimensional figures.

Tell whether each of the following statements describes Figure A, Figure B, both, or neither.

Figure A triangular prism. Figure B triangular pyramid.
  1. This figure is a polyhedron.
  2. This figure has triangular faces.
  3. There are more vertices than edges in this figure.
  4. This figure has rectangular faces.
  5. This figure is a pyramid.
  6. There is exactly one face that can be the base for this figure.
  7. The base of this figure is a triangle.
  8. This figure has two identical and parallel faces that can be the base.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 13.)

Problem 5

Select all units that can be used for surface area. 

A:

square meters

B:

feet

C:

centimeters

D:

cubic inches

E:

square inches

F:

square feet

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 12.)

Problem 6

Find the area of this polygon. Show your reasoning.

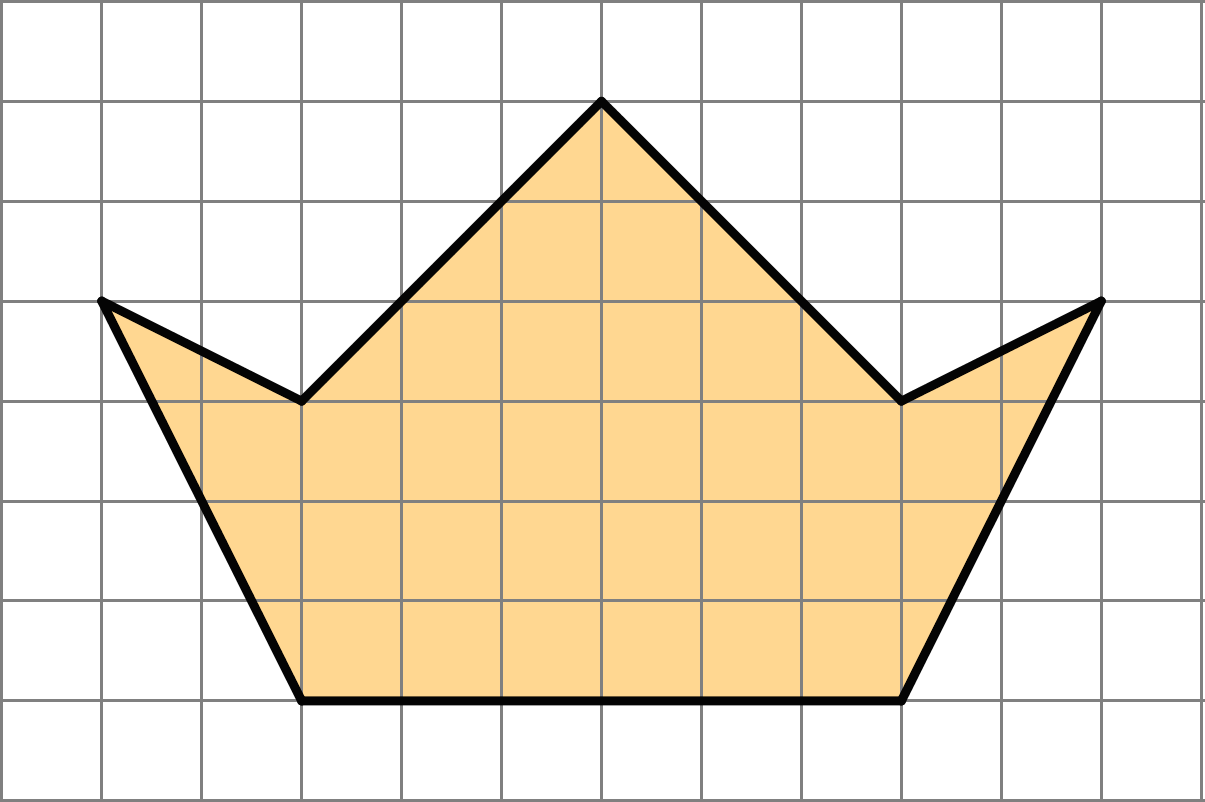
An image of a 7-sided polygon. The bottom side of the polygon is six units long, and extends out to a total width of 10 units, and a central height of 6 units.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 11.)