Lesson 13
Polyhedra
Lesson Narrative
In this lesson, students learn about polyhedra and their nets. They also study prisms and pyramids as types of polyhedra with certain defining features.
Polyhedra can be thought of as the three-dimensional analog of polygons.
Here are some important aspects of polygons:
- They are made out of line segments called edges.
- Edges meet at a vertex.
- The edges only meet at vertices.
- Polygons always enclose a two-dimensional region.
Here is an analogous way to characterize polyhedra:
- They are made out of filled-in polygons called faces.
- Faces meet at an edge.
- The faces only meet at edges.
- Polyhedra always enclose a three-dimensional region.
Students do not need to memorize a formal definition of a polyhedron, but help them make sense of nets and surface area.
Learning Goals
Teacher Facing
- Compare and contrast (orally and in writing) features of prisms and pyramids.
- Comprehend and use the words “face”, “edge”, “vertex”, and “base” to describe polyhedra (in spoken and written language).
- Understand that the word “net” refers to a two-dimensional figure that can be assembled into a polyhedron, and create a net for a given polyhedron.
Student Facing
Let’s investigate polyhedra.
Required Materials
Required Preparation
- Assemble collections of geometric figures that each contains at least 2 familiar polyhedra, 2 unfamiliar polyhedra, and 2 non-polyhedra. Prepare one collection for each group of 3–4 students. If pre-made polyhedra are unavailable, assemble some from the nets in the blackline master for the warm-up.
- Print and pre-cut the nets and polygons in the blackline master for Prisms and Pyramids. Prepare 1 set per group of 3–4 students, along with tape to join the polygons into a net.
- For the optional Assembling Polyhedra activity, print the nets from the same blackline master as for the warm-up. Prepare 2 copies of one net per student, and tape or glue to assemble the net.
Learning Targets
Student Facing
- I can describe the features of a polyhedron using mathematical vocabulary.
- I can explain the difference between prisms and pyramids.
- I understand the relationship between a polyhedron and its net.
Glossary Entries
-
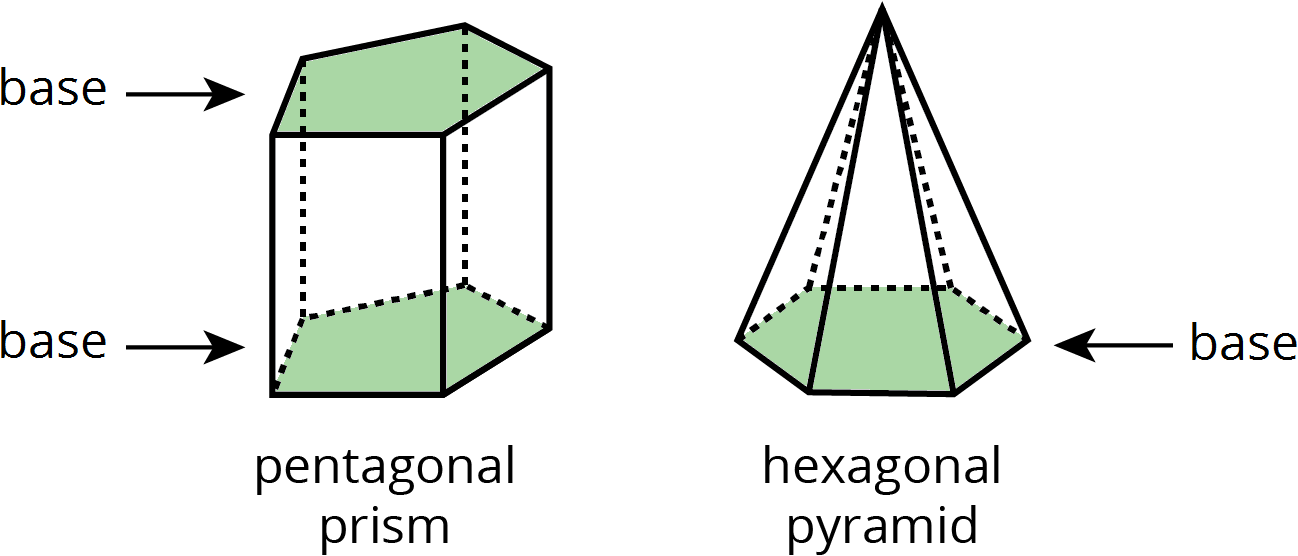
base (of a prism or pyramid)
The word base can also refer to a face of a polyhedron.
A prism has two identical bases that are parallel. A pyramid has one base.
A prism or pyramid is named for the shape of its base.
-
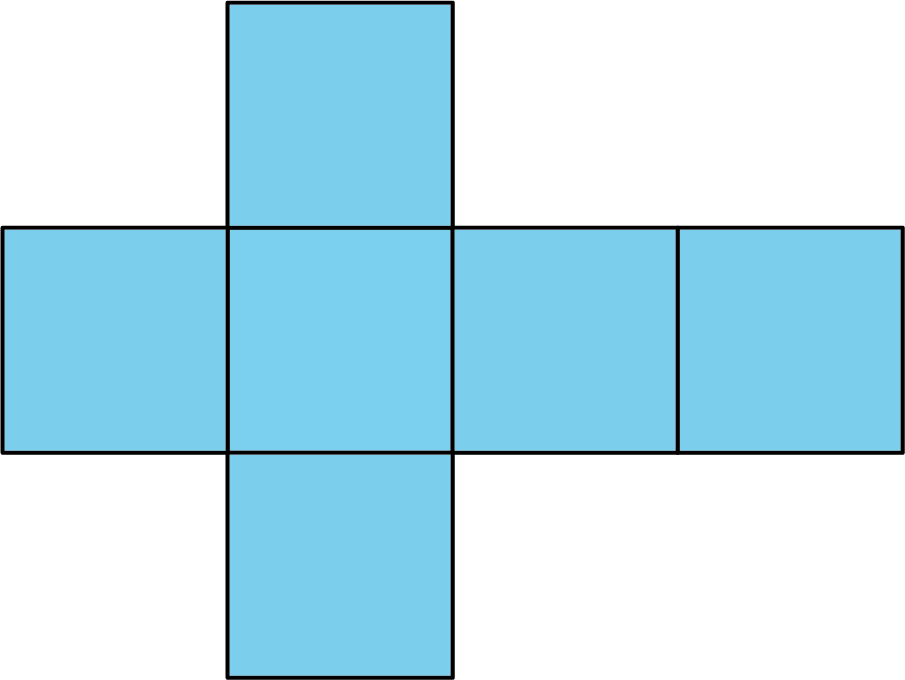
net
A net is a two-dimensional figure that can be folded to make a polyhedron.
Here is a net for a cube.
-
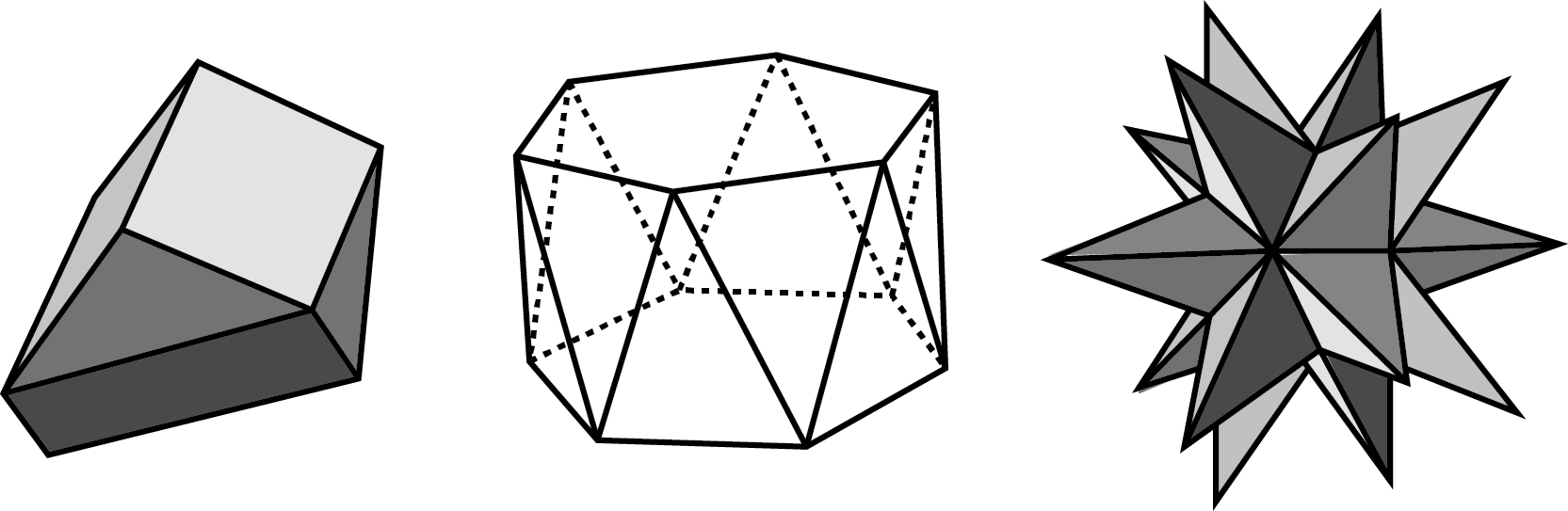
polyhedron
A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.
Here are some drawings of polyhedra.
-
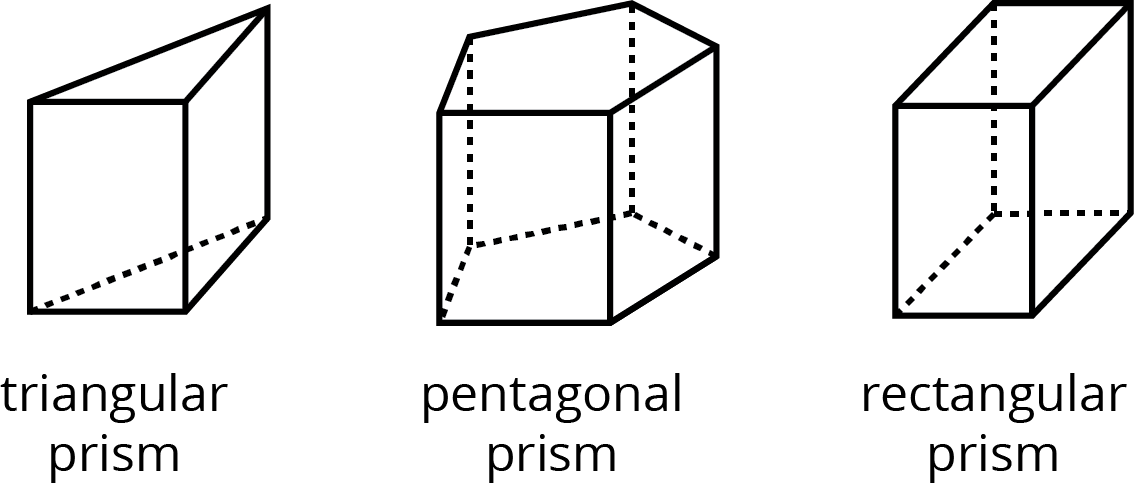
prism
A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.
Here are some drawings of prisms.
-
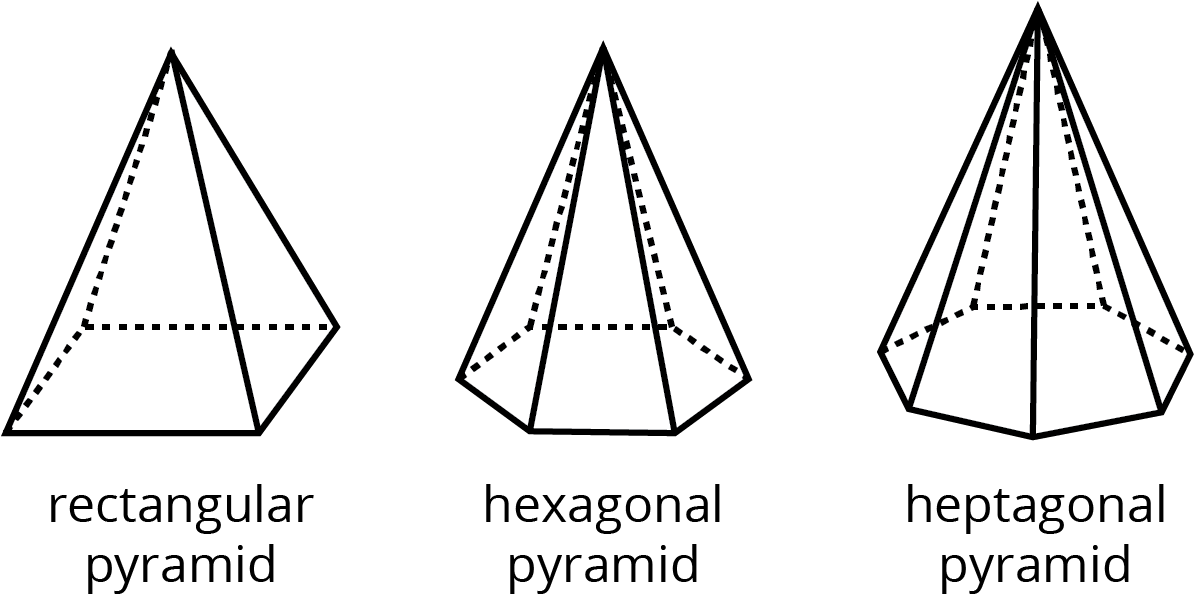
pyramid
A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.
Here are some drawings of pyramids.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |