Lesson 10

Bases and Heights of Triangles

View Student Lesson

Lesson Narrative

This lesson furthers students’ ability to identify and work with a base and height in a triangle in two ways:

  1. By learning to draw (not just to recognize) a segment to show the corresponding height for any given base, and

  2. By learning to choose appropriate base-height pairs to enable area calculations.

Students have seen that the area of a triangle can be determined in multiple ways. Using the base and height measurements and the formula is a handy approach, but because there are three possible pairs of bases and heights, some care is needed in identifying the right combination of measurements. Some base-height pairs may be more practical or efficient to use than others, so it helps to be strategic in choosing a side to use as a base.


Learning Goals

Teacher Facing

  • Draw and label the height that corresponds to a given base of a triangle, making sure it is perpendicular to the base and the correct length.
  • Evaluate (orally) the usefulness of different base-height pairs for finding the area of a given triangle.

Student Facing

Let’s use different base-height pairs to find the area of a triangle.

Required Materials

Required Preparation

From the geometry toolkit, each student especially needs an index card for the Hunting for Heights activity.

Learning Targets

Student Facing

  • I can identify pairs of base and corresponding height of any triangle.
  • When given information about a base of a triangle, I can identify and draw a corresponding height.

CCSS Standards

Addressing

Glossary Entries

  • edge

    Each straight side of a polygon is called an edge.

    For example, the edges of this polygon are segments \(AB\), \(BC\), \(CD\), \(DE\), and \(EA\).

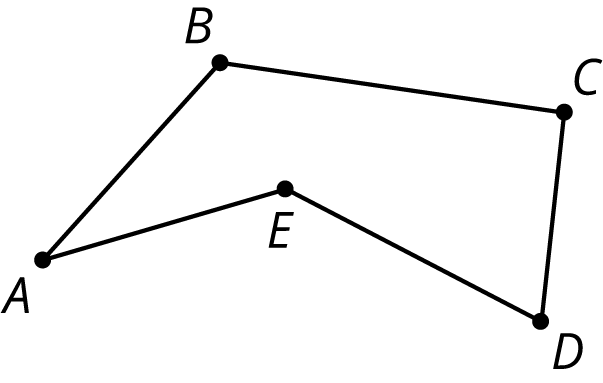
    Polygon with 5 sides
  • vertex

    A vertex is a point where two or more edges meet. When we have more than one vertex, we call them vertices.

    The vertices in this polygon are labeled \(A\), \(B\), \(C\), \(D\), and \(E\).

    Polygon with 5 sides

Print Formatted Materials

For access, consult one of our IM Certified Partners.

Additional Resources

Google Slides

For access, consult one of our IM Certified Partners.
PowerPoint Slides

For access, consult one of our IM Certified Partners.