Lesson 13
Median
13.1: The Plot of the Story (5 minutes)
Warm-up
This warm-up reinforces students’ understanding about the relationship between the mean absolute deviation (MAD) and the spread of data. In the given scenarios, the number of people attending the two events and their mean age are the same, but the MADs are different. In the first question, students interpret these measures in the context of the situations. In the second, they draw a dot plot that could represent an age distribution with the same mean and yet another MAD.
As students work and discuss, identify several students who drew dot plots that correctly meet the criteria in the second question. Ask students with different dot plots to share during whole-class discussion.
Students may need more time to make sense of how to generate their own dot plot for the second question. If it is not possible to give students additional time, consider presenting the second question at a different time.
Launch
Arrange students in groups of 2. Give students 1 minute of quiet think time for the first question, and then 2–3 minutes to work on the second question with a partner. Display the following questions for all to see. Ask students to think about and discuss them before drawing their dot plots:
- “How many data points should be on the dot plot?”
- “How would the mean help us place the data points?”
- “How would the MAD help us place the data points?”
- “How should our dot plot compare to the dot plots of data sets A and B?”
Student Facing
-
Here are two dot plots and two stories. Match each story with a dot plot that could represent it. Be prepared to explain your reasoning.
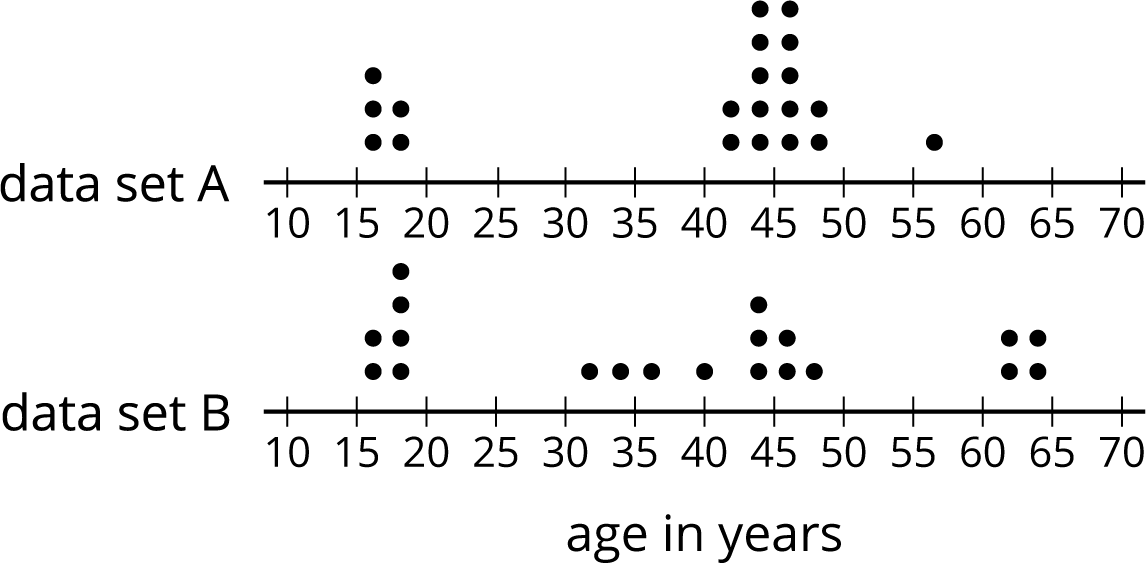
-
Twenty people—high school students, teachers, and invited guests—attended a rehearsal for a high school musical. The mean age was 38.5 years and the MAD was 16.5 years.
- High school soccer team practice is usually watched by supporters of the players. One evening, twenty people watched the team practice. The mean age was 38.5 years and the MAD was 12.7 years.
-
- Another evening, twenty people watched the soccer team practice. The mean age was similar to that from the first evening, but the MAD was greater (about 20 years).
Make a dot plot that could illustrate the distribution of ages in this story.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Poll students on their response to the first question. Ask a student to explain how they matched one context to its dot plot and another student to explain the second matching context and dot plot. Record and display their responses for all to see. If possible, record their responses directly on the dot plots.
Ask selected students to share their dot plots for the second question and their reasoning. To involve more students in the conversation, consider asking some of the following questions:
- “What was the first piece of information you used to draw your dot plot? Why?”
- “How did you decide where to place your dots?”
- “How is your dot plot the same or different than the first evening of soccer practice?”
- “Do you agree or disagree with this representation of the context? Why?”
- “Do you have any questions to ask the student who drew the dot plot?”
13.2: Siblings in the House (15 minutes)
Activity
The aim of this activity is to expose the limits of the mean in summarizing a data set that has gaps and values far from the center, and to motivate a need to have another measure of center. Students first use a table of values and a dot plot to estimate a “typical” value for a data set. Then, they calculate the mean and notice that it does not match their estimate of a typical value. A closer look helps them see that when a data set contains values that are far away from the bulk of the data, or when there are gaps in the data set, the mean can be a little or a lot higher or lower than what we would consider typical for the data.
In the next activity, the median will be introduced as another measure of center of a data set.
Launch
Arrange students in groups of 2. Give students 7–8 minutes of quiet work time and then 3–4 minutes to discuss their responses with a partner. If there are disagreements, ask them to discuss them until they reach agreement. Follow with a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Here is data that shows the numbers of siblings of ten students in Tyler’s class.
1
0
2
1
7
0
2
0
1
10
- Represent the data shown with a dot plot.
-
Without making any calculations, estimate the center of the data based on your dot plot. What is a typical number of siblings for these sixth-grade students? Mark the location of that number on your dot plot.
- Find the mean. Show your reasoning.
-
- How does the mean compare to the value that you marked on the dot plot as a typical number of siblings? (Is it a little larger, a lot larger, exactly the same, a little smaller, or a lot smaller than your estimate?)
-
Do you think the mean summarizes the data set well? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Invent a data set with a mean that is significantly lower than what you would consider a typical value for the data set.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Since previous lessons have used the mean as the best way to find a typical value, some students may go directly to that method from the beginning. Although this is valid at this stage, encourage them to look at the dot plot and think about what a typical value should be.
Activity Synthesis
Select a few students to share their estimate for a typical number of siblings. Consider asking students:
- “When you looked at the table of values, what was your sense of a typical number of siblings for the ten students in Tyler's class?”
- “When you looked at the dot plot, did your estimate change?”
Then, discuss how the calculated mean compared to their estimates. Draw students’ attention to the idea that the mean may not always represent a typical value for a data set. Discuss:
- “We have learned that the mean is a way to measure the center of a distribution. How did your calculated mean compare to your estimate of what was typical for the data set?”
- “Why do you think the mean was higher than your estimate?” (Only two of the points are above the mean of 2.4 and both are quite far above it, and seven points are below 2.4, so the mean might not paint an accurate picture of what is typical in this situation.)
- “If the mean does not always reflect what is typical in a data set, should we always rely on it as the best way to describe the center? If not, in what other ways might we measure the center of a data set?”
Explain to students that in the next activity we will look at a different measure of center.
Design Principle(s): Optimize output (for generalization); Cultivate conversation
13.3: Finding the Middle (15 minutes)
Activity
This activity introduces students to the term median. They learn that the median describes the middle value in an ordered list of data, and that it can capture what we consider typical for the data in some cases.
Students learn about the median through a kinesthetic activity. They line up in order of the number of letters in their name. Then, those at both ends of the line count off and sit down simultaneously until one or two people in the middle remain standing. If one person remains standing, that person has the median number of letters. If two people remain standing, the median is the mean or the average of their two values.
Students then practice identifying the median of other data sets, by analyzing both tables of values and dot plots.
Launch
Explain to students that, instead of using the mean, sometimes we use the “middle” value in an ordered list of data set as a measure of center. We call this the median. Guide students through the activity:
-
Give each student an index card. Ask them to write their first and last names on the card and record the total number of letters in their name. Display an example for all to see.
-
Ask students to stand up, holding their index cards in front of them, and arrange themselves in order based on the number of letters in their name. (Consider asking students to do so without speaking at all.) Look for the student whose name has the fewest letters and ask him or her to be the left end of the line. Ask the student with the longest full name to be the right end of the line. Students who have the same number of letters should stand side-by-side.
-
Tell students that, to find the median or the middle number, we will count off from both ends at the same time. Ask the students at the two ends of the line say “1” at the same time and sit on the floor, and the students next to them to say “2” and then sit down, and so on. Have students count off in this fashion until only one or two students are standing.
-
If the class has an odd number of students, one student will remain standing. Tell the class that this student’s number is the median. Give this student a sign that says “median” If the class has an even number of students, two students will remain standing. The median will be the mean or average of their numbers. Ask both students to hold the sign that says “median.” Explain that the median is also called the “50th percentile,” because half of the data values are the same size or less than it and fall to the left of it on the number line, and half are the same size or greater than it and fall to the right.
-
Ask students to find the median a couple more times by changing the data set (e.g., asking a few students to leave the line or adding new people who are not members of the class with extremely long or short names). Make sure that students have a chance to work with both odd and even numbers of values.
-
Collect the index cards and save them; they will be used again in the lesson on box plots.
Ask students to complete the rest of the questions on the task statement.
Supports accessibility for: Memory; Language
Student Facing
-
Your teacher will give you an index card. Write your first and last names on the card. Then record the total number of letters in your name. After that, pause for additional instructions from your teacher.
-
Here is the data set on numbers of siblings from an earlier activity.
1
0
2
1
7
0
2
0
1
10
- Sort the data from least to greatest, and then find the median.
- In this situation, do you think the median is a good measure of a typical number of siblings for this group? Explain your reasoning.
-
Here is the dot plot showing the travel time, in minutes, of Elena’s bus rides to school.

- Find the median travel time. Be prepared to explain your reasoning.
- What does the median tell us in this context?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
When determining the median, students might group multiple data points that have the same value and treat it as a single point, instead of counting each one separately. Remind them that when they lined up to find the median number of letters in their names, every student counted off, even their name has the same number of letters as their neighbors.
Activity Synthesis
Select a few students to share their responses to the questions about number of siblings and Elena's travel times. Focus the discussion on the median as another measure of the center of a data set and whether it captures what students would estimate to be a typical value for each data set.
Emphasize to students that the median is a value and not an individual. For example, if the last person standing in the class has 5 letters in their first name, the median is the number 5 and not the person standing. If there is another student who had 5 letters in their name, they might have switched places with the last person standing when lining up initially. Although the person standing changed, the median remains the same value of 5.
At this point, it is unnecessary to compare the mean and the median. Students will have many more opportunities to explore the median and think about how it differs from the mean in the upcoming activities.
Design Principle(s): Cultivate conversation; Maximize meta-awarenes
Lesson Synthesis
Lesson Synthesis
In this lesson, we learn about another measure of center called the median. The discussion should focus on what the median is, how to find it, and why it is useful.
- “What is the median?” (The number in the middle of an ordered list of data.)
- “How can we find it?” (We order the data values from least to greatest and find the value in the middle.)
- “Is the median always one of the values in the data set? If not, when is it not?” (No. When the number of values in a data set is even, there will be two middle values. The median is the number exactly between them which may not be a value in the data set.)
- “What does the median tell you about a data set? Why is it used as a measure of the center of a distribution?” (It tells us where to divide a data set so that half of the data points have that value or smaller values and the other half have that value or larger.)
- “Why do we need another measure of center other than the mean?” (Sometimes the mean is not a good indication of what is typical for the data set.)
13.4: Cool-down - Practicing the Piano (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The median is another measure of center of a distribution. It is the middle value in a data set when values are listed in order. Half of the values in a data set are less than or equal to the median, and half of the values are greater than or equal to the median.
To find the median, we order the data values from least to greatest and find the number in the middle.
Suppose we have 5 dogs whose weights, in pounds, are shown in the table. The median weight for this group of dogs is 32 pounds because three dogs weigh less than or equal to 32 pounds and three dogs weigh greater than or equal to 32 pounds.
20
25
32
40
55
Now suppose we have 6 cats whose weights, in pounds, are as shown in the table. Notice that there are two values in the middle: 7 and 8.
4
6
7
8
10
10
The median weight must be between 7 and 8 pounds, because half of the cats weigh less or equal to 7 pounds and half of the cats weigh greater than or equal to 8 pounds.
In general, when we have an even number of values, we take the number exactly in between the two middle values. In this case, the median cat weight is 7.5 pounds because \((7+8)\div 2=7.5\).