Lesson 1
Got Data?
1.1: Dots of Data (10 minutes)
Warm-up
The purpose of this warm-up is to review students’ prior knowledge about Representation of numerical data. Students may be familiar with line plot from previous grades but unfamiliar with the term dot plot, which is what will be used in this unit and beyond. Students learn that both terms are commonly used for the same type of diagram.
Students examine a dot plot of data and consider which contexts may make sense for the data shown. Then students invent their own context for the data and interpret what additional data in that set would mean in their context.
This is an opportunity to see how students make sense of a data representation in the context of situations (MP2), which is central to the work of the unit.
Launch
Display the image for all to see.
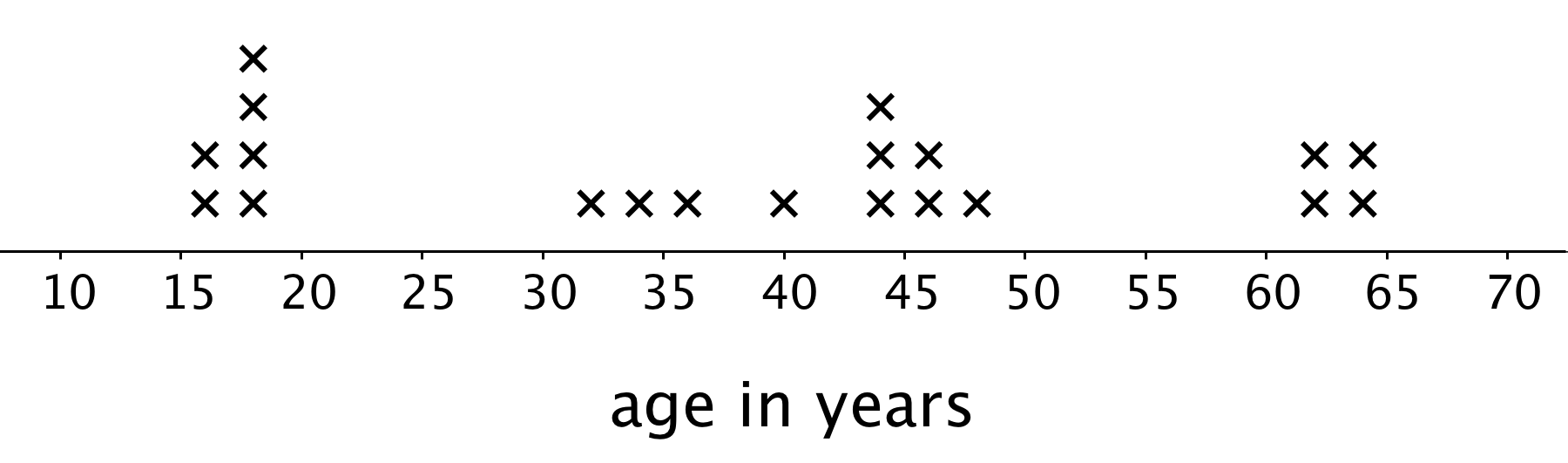
Ask students what they notice and wonder about the image. Students should notice:
- The numbers represent age based on the label.
- Each X represents one person. For example, it looks like there is 1 40-year old represented but 3 44-year olds.
- There are a total of 20 people represented.
Students may wonder:
- Why are these people important?
- Why is there such a large age range?
- Why is there nobody in their 20s represented?
If not mentioned by students, remind them that the display is a line plot. Tell students that in the task they will see and use the same type of representation, but it is called a dot plot, and that dots are used instead of Xs.
Give students 2 minutes of quiet work time to complete the task, followed by a whole-class discussion.
Student Facing
Here is a dot plot for a data set.

-
Determine if each of the following would be an appropriate label to represent the data in the dot plot? Be prepared to explain your reasoning.
- Number of children per class.
- Distance between home and school, in miles.
- Hours spent watching TV each day.
- Weight of elephants, in pounds.
- Points received on a homework assignment.
-
Think of another label that can be used with the dot plot.
- Write it below the scale of the dot plot. Be sure to include the unit of measurement.
- In your scenario, what does one dot represent?
- In your scenario, what would a data point of 0 mean? What would a data point of \(3\frac 14\) mean?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to understand how to read a dot plot including what dots represent in context.
Poll students on their responses to each scenario presented in the first question and ask a few students to explain their reasoning for each. After each student shares their explanation, ask the class if they agree or disagree and why.
Invite a few students to share another label they think could be used with the set of data and what each dot would represent. Based on each response, ask the class the following the questions:
- “What would a data point of 0 mean in the context mentioned?”
- “What would a data point of \(3\frac 14\) mean in the context mentioned?”
1.2: Surveying the Class (20 minutes)
Activity
Students begin their statistical explorations with data collection. They answer several survey questions, take some measurements, or do both. This data gathering activity serves several purposes: to give students firsthand experience in gathering and organizing data, to prompt students to notice different types of data that could be collected, and to provide the class with authentic data that can later be analyzed as students gain and expand the skills to do so.
The task statements show a range of survey questions and ideas for collecting measurements. To optimize the data gathering, have several survey questions and measuring activities identified ahead of time and consider how to best collect the responses or measurements.
Launch
Explain to students that they will gather data to learn more about the students in the class. Tell them which data sets will be collected and give instructions on the collection process. If students are to do a gallery walk or rotate through measuring stations, consider arranging them into groups of 3–4 to facilitate the rotation.
Supports accessibility for: Organization; Attention
Student Facing
Here are some survey questions. Your teacher will explain which questions can be used to learn more about the students in your class and how the responses will be collected. The data that your class collects will be used in upcoming activities.
- How long does it usually take you to travel to school? Answer to the nearest minute.
-
How do you travel to school on most days? Choose one.
- Walk
- Bike
- Scooter or skateboard
- Car
- School bus
- Public transport
- Other
- How tall are you without your shoes on? Answer to the nearest centimeter.
- What is the length of your right foot without your shoe on? Answer to the nearest centimeter.
- What is your arm span? Stretch your arms open, and measure the distance from the tip of your right hand’s middle finger to the tip of your left hand’s middle finger, across your back. Answer to the nearest centimeter.
-
How important are the following issues to you? Rate each on a scale from 0 (not important) to 10 (very important).
- Reducing pollution
- Recycling
-
Conserving water
-
Do you have any siblings? _____ Yes _____ No
- How many hours of sleep per night do you usually get when you have school the next day? Answer to the nearest half hour.
- How many hours of sleep per night do you usually get when you do not have school the next day? Answer to the nearest half hour.
-
Other than traveling from school, what do you do right after school on most days?
- Have a snack
- Do homework
- Read a book
- Talk on the phone
- Practice a sport
- Do chores
- Use the computer
- Participate in an extracurricular activity
-
If you could meet one of these celebrities, who would you choose?
- A city or state leader
- A champion athlete
- A movie star
- A musical artist
- A best-selling author
-
Estimate how much time per week you usually spend on each of these activities. Answer to the nearest quarter of an hour.
- Playing sports or doing outdoor activities
- Using a screen for fun (watching TV, playing computer games, etc.)
- Doing homework
- Reading
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
When taking measurements, students might not remember to attend to the right units, to start from 0, or to hold the measuring tool so that measurements can be precisely taken. Remind students about these issues as needed.
Activity Synthesis
Tell students to put their responses to the selected questions in the appropriate place in the room. Allow them to do a gallery walk of the data sets discussing with their group things they notice about each question. After students have had a chance to view the data, draw their attention to the twelve survey questions in the task statements. Ask them to think about the types of responses they produce. Students are likely to notice that responses to some questions are numbers and others are not. Explain that responses that are measurements or quantities are called numerical data. For example, the first question about the travel time to school produces numerical data because the responses are quantities, measured in minutes.
Point out that responses to other questions are not quantities but can be sorted into categories. Explain that these types of responses are called categorical data. For example, the second question about ways of traveling to school produces categorical data because the responses can be sorted into categories.
Explain that numerical and categorical data will continue to be investigated in upcoming lessons.
The data from the first three questions regarding travel time, travel method, and height will be used in future lessons. Collect this data in an organized way to redistribute and use with students later.
Design Principle(s): Optimize output (for describing); Support sense-making
1.3: Numerical and Categorical Data (10 minutes)
Activity
In the previous activity, students responded to survey questions and collected data. They learned that data can be categorical or numerical. In this activity, students practice distinguishing categorical and numerical data, using the same survey questions and additional ones. They think about the kind of responses these questions would yield. For numerical responses, they consider the units of measurement. For categorical responses, they identify the characteristic being studied.
Note that some data may have numbers for their values but are categorical rather than numerical. Area codes and zip codes are examples of such categorical data. They are not quantities or measurements, but rather labels that happen to be numbers. We can meaningfully compare quantities or measurements (e.g., 6 minutes is greater than 4 minutes, or 7 years is less than 12 years), but we cannot do the same with the numbers in area codes or zip codes. It would not make sense to say, for example, that the zip code is 19104 is less than 63105.
As students work and discuss, notice students who could succinctly articulate the variables being investigated in both numerical and categorical questions. Also notice any disagreements partners might have about whether a question results in numerical or categorical data. The sixth survey question (rating the importance of environmental issues) and last survey question (hours spent on out-of-school activities) are likely to generate conversations as they may appear less straightforward than the others.
Launch
Arrange students in groups of 2. Tell students they will need the list of survey questions from the previous activity. Give them 3–4 minutes of quiet work time to complete the first three questions. Ask them to briefly discuss their responses with their partner before completing the last question.
Supports accessibility for: Language; Organization
Student Facing
The list of survey questions in the activity earlier can help you complete these exercises.
-
The first survey question about travel time produces numerical data. Identify two other questions that produce numerical data. For each, describe what was measured and its unit of measurement.
-
Question #: ______
What was measured:
Unit of measurement:
-
Question #: ______
What was measured:
Unit of measurement:
-
-
The second survey question about travel method produces categorical data. Identify two other questions that produce categorical data. For each, describe what characteristic or feature was being studied.
-
Question #: ______
Characteristic being studied:
-
Question #: ______
Characteristic being studied:
-
-
Think about the responses to these survey questions. Do they produce numerical or categorical data? Be prepared to explain how you know.
- How many pets do you have?
- How many years have you lived in this state?
- What is your favorite band?
- What kind of music do you like best?
- What is the area code of your school’s phone number?
- Where were you born?
- How much does your backpack weigh?
- Name two characteristics you could investigate to learn more about your classmates. Make sure one would give categorical data and the other would give numerical data.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Priya and Han collected data on the birth months of students in their class. Here are the lists of their records for the same group of students.
This list shows Priya’s records.
- Jan
- Apr
- Jan
- Feb
- Oct
- May
- June
- July
- Aug
- Aug
- Sep
- Jan
- Feb
- Mar
- Apr
- Nov
- Nov
- Dec
- Feb
- Mar
This list shows Han’s records.
- 1
- 4
- 1
- 2
- 10
- 5
- 6
- 7
- 8
- 8
- 9
- 1
- 2
- 3
- 4
- 11
- 11
- 12
- 2
- 3
- How are their records alike? How are they different?
- What kind of data—categorical or numerical—do you think the variable “birth month” produces? Explain how you know.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may mistake numbers such as area codes, zip codes, or the numbers we use to represent months (e.g., 1 for January) as numerical data. Be sure to discuss this common confusion if arises. See the Activity Narrative section for ideas for addressing it.
Activity Synthesis
The purpose of the discussion is for students to be able to identify data collected as either numerical or categorical.
Select a few previously identified students to share their responses to the first two questions. After each student shares, ask the rest of the class if they agree or disagree and discuss any disagreements. Then, poll the class on their responses to the third set of questions. If not mentioned by students, explain how some categorical data are comprised of numbers, as noted in the Activity Narrative section.
Lesson Synthesis
Lesson Synthesis
In this lesson, we collected and explored different types of data. We noticed that certain survey questions produce responses that are quantities or measurements; we call these responses numerical data. Other questions produce responses that are not measurements or quantities but can be sorted into categories; we call these categorical data.
- “What are some examples of categorical data?”
- “What are some examples of numerical data?”
- “What is a dot plot?” (A dot plot is a representation of numerical data.)
- “How does it represent data?” (It represents each data value with a point above a number line.)
Consider creating a permanent display of the vocabulary throughout the unit including numerical data, categorical data, and dot plot for this lesson.
1.4: Cool-down - What’s the Question? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The table contains data about 10 dogs.
| dog name | weight (kg) | breed |
|---|---|---|
| Duke | 36 | German shepherd |
| Coco | 6 | pug |
| Pierre | 7 | pug |
| Ginger | 35 | German shepherd |
| Lucky | 10 | beagle |
| Daisy | 10 | beagle |
| Buster | 35 | German shepherd |
| Pepper | 7 | pug |
| Rocky | 7 | beagle |
| Lady | 32 | German shepherd |
- The weights of the dogs are an example of numerical data, which is data that are numbers, quantities, or measurements. The weights of the dogs are measurements in kilograms.
- The dog breeds are an example of categorical data, which is data containing values that can be sorted into categories. In this case, there are three categories for dog breeds: pug, beagle, and German shepherd.
Some data with numbers are categorical because the numbers are not quantities or measurements. For example, telephone area codes are categorical data, because the numbers are labels rather than quantities or measurements.
Numerical data can be represented with a dot plot (sometimes called a line plot). Here is a dot plot that shows the weights of the dogs.
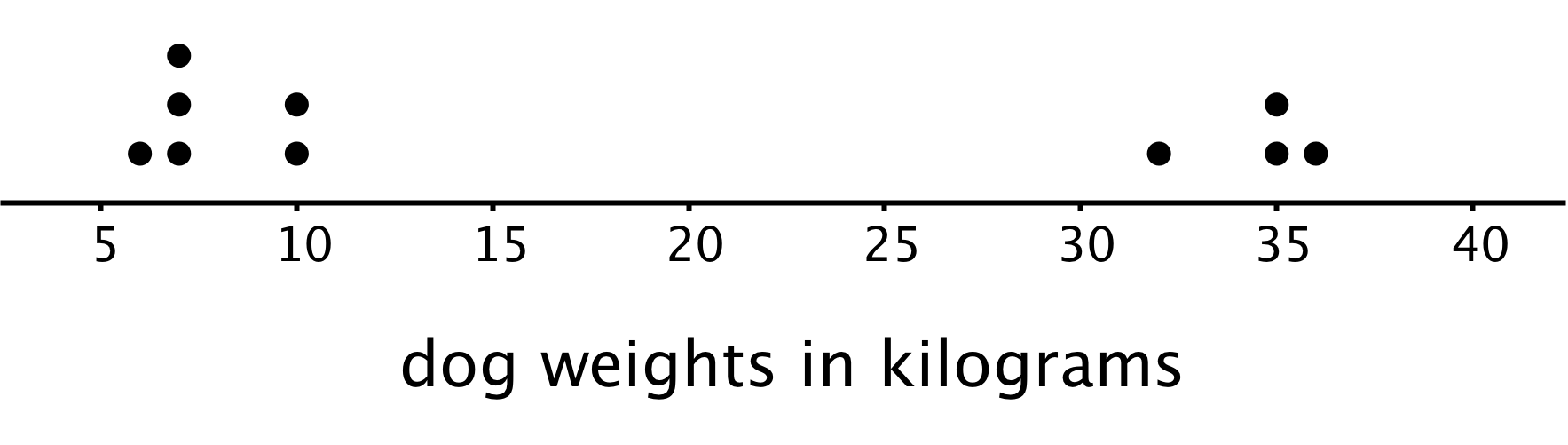
We can collect and study both kinds of data by doing surveys or taking measurements. When we do, it is important to think about what feature we are studying (for example, breeds of dogs or weights of dogs) and what units of measurement are used.