Lesson 4
Dot Plots
4.1: Pizza Toppings (Part 1) (5 minutes)
Warm-up
This warm-up serves two purposes. It prompts students to determine when a dot plot is an appropriate representation and allows students to practice organizing data into a frequency table. The table completed in this activity will be used in the following activity in this lesson.
Launch
Arrange students in groups of 2. Give students 2 minutes to complete the activity with a partner, and then another 1–2 minutes for them to compare their frequency tables with another group.
Student Facing
Fifteen customers in a pizza shop were asked, “How many toppings did you add to your cheese pizza?” Here are their responses:
- 1
- 2
- 1
- 3
- 0
- 1
- 1
- 2
- 0
- 3
- 0
- 0
- 1
- 2
- 2
- Could you use a dot plot to represent the data? Explain your reasoning.
-
Complete the table.
number of toppings frequency (number) 0 1 2 3
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask a couple of students to share their responses to the first question and poll the class for their agreement or disagreement.
4.2: Pizza Toppings (Part 2) (10 minutes)
Activity
After organizing the data set into a frequency table in the warm-up, students now represent the information graphically. The drawing of the plot should be fairly straightforward. The emphasis here is on using a graphical representation to study and comment on the data distribution, and to reinforce how it allows us to make observations that are difficult to make by looking at lists and tables.
As students work, identify those who describe distributions not only in terms of individual categories or values (e.g. “four people did not order any toppings”) but also characterize them in broader terms (e.g. “almost all customers in the data set ordered 2 or fewer toppings”). Invite them to share during the discussion following the activity.
Launch
Keep students in groups of 2. Give students 4–5 minutes of quiet work time and 1–2 minutes to share their responses with a partner.
Supports accessibility for: Language; Organization
Student Facing
-
Use the tables from the warm-up to display the number of toppings as a dot plot. Label your drawing clearly.
- Use your dot plot to study the distribution for number of toppings. What do you notice about the number of toppings that this group of customers ordered? Write 2–3 sentences summarizing your observations.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Think of a statistical question that can be answered with the data about the number of toppings ordered, as displayed on the dot plot. Then answer this question.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Display a completed dot plot for all to see. Solicit as many observations or comments about the distribution as time permits. The goal of this discussion is to allow students to hear as many ways to describe distributions as possible. Be sure to select previously identified students to make observations that succinctly capture the distributions.
4.3: Homework Time (20 minutes)
Activity
In the previous activity, students commented on distributions on a dot plot and had opportunities to hear different ways to describe distributions. In this activity, they begin to think about how to characterize a distribution as a whole, in terms of its center and spread. Students learn that we can give a general description of a distribution by identifying a location that could be the center of the data, and by noting how alike or different the data points are.
Note that at this point “center” and “spread” can only be identified and described informally, via visual observation and intuitive reasoning about how data points are distributed. The lack of precise ways to identify center and spread helps to cultivate the need for more formal measures later.
In this activity, students evaluate and critique another's reasoning (MP3).
Launch
Keep students in groups of 2. Ask students to read the question in the stem, “How many hours do you generally spend on homework each week?” Then, ask students to explain why this is a statistical question. This is a statistical question because it can be answered by collecting data, and we can expect variability in the data.
Give them 6–7 minutes of quiet time to work on the first three questions, and then 4–5 minutes to share their responses with their partner and to complete the last two questions together. Be sure to leave at least 5 minutes for a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Twenty-five sixth-grade students answered the question: “How many hours do you generally spend on homework each week?”
This dot plot shows the number of hours per week that these 25 students reported spending on homework.

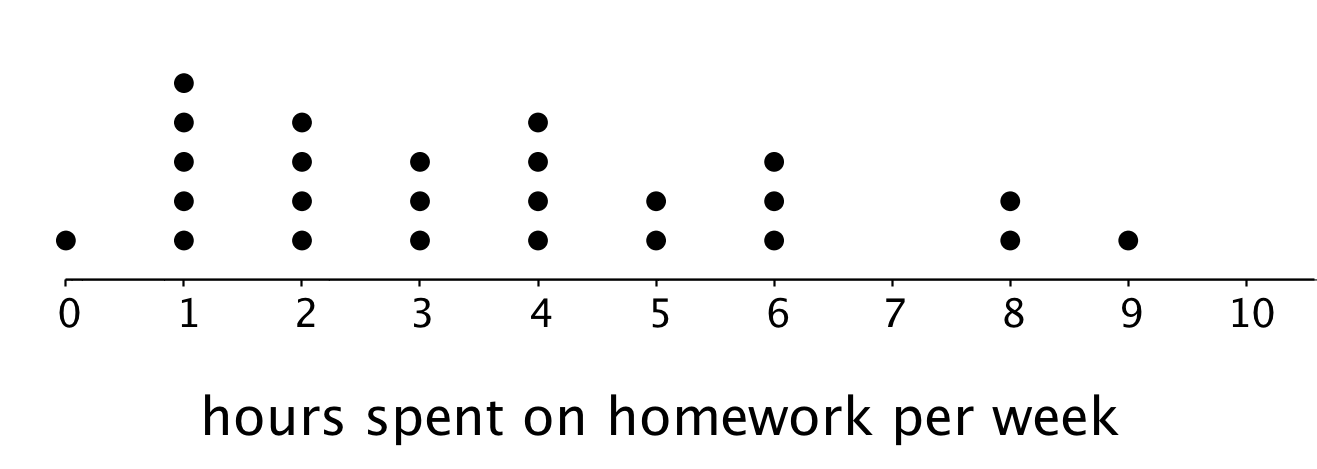
Use the dot plot to answer the following questions. For each, show or explain your reasoning.
- What percentage of the students reported spending 1 hour on homework each week?
- What percentage of the students reported spending 4 or fewer hours on homework each week?
- Would 6 hours per week be a good description of the number of hours this group of students spends on homework per week? What about 1 hour per week? Explain your reasoning.
- What value do you think would be a good description of the homework time of the students in this group? Explain your reasoning.
-
Someone said, “In general, these students spend roughly the same number of hours doing homework.” Do you agree? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not recall how to find a percentage. Remind them that a percentage can be found if we know the size of a part and that of a whole. If needed, prompt them to determine the size of the entire data set.
Activity Synthesis
Ask a couple of students to share their thinking on what number of hours would be a good description of homework time for this group of students and why. Then, select a couple of other students to discuss how alike or different the lengths of homework time are.
Explain that sometimes it helps to describe a set of data generally, or to characterize it as a whole. One way to do that is by finding a value that describes the whole set reasonably well, or a value whose location can be considered the “center” of a distribution. Ask students:
- “Where on the dot plot would you consider the center of the data? What is the value of that center?”
Another way to characterize a data set is by describing its “spread,” or the variability in the data points. The wider the spread (the more dispersed the data points are on a dot plot), the more variable or different they are. The narrower the spread (the more clustered together), the more alike they are. Ask students:
- “Based on the dot plot, how would you describe the spread of the students’ homework time? Are the amounts of time they spend on homework alike or different?”
Tell students that we will continue to explore center and spread in upcoming lessons.
Design Principle(s): Maximize meta-awareness, Cultivate conversation
Lesson Synthesis
Lesson Synthesis
In this lesson, we look closely at data sets and try to describe what is typical for the data set. We notice that if we study the distribution of data, we can find out what is typical or common.
- What does the term “typical” mean? When someone wants to find out “a typical height of sixth-graders,” what is the information of interest?
- How do tell what is typical from a dot plot such as this one? How might we describe the characteristics of this data set on dog weights?
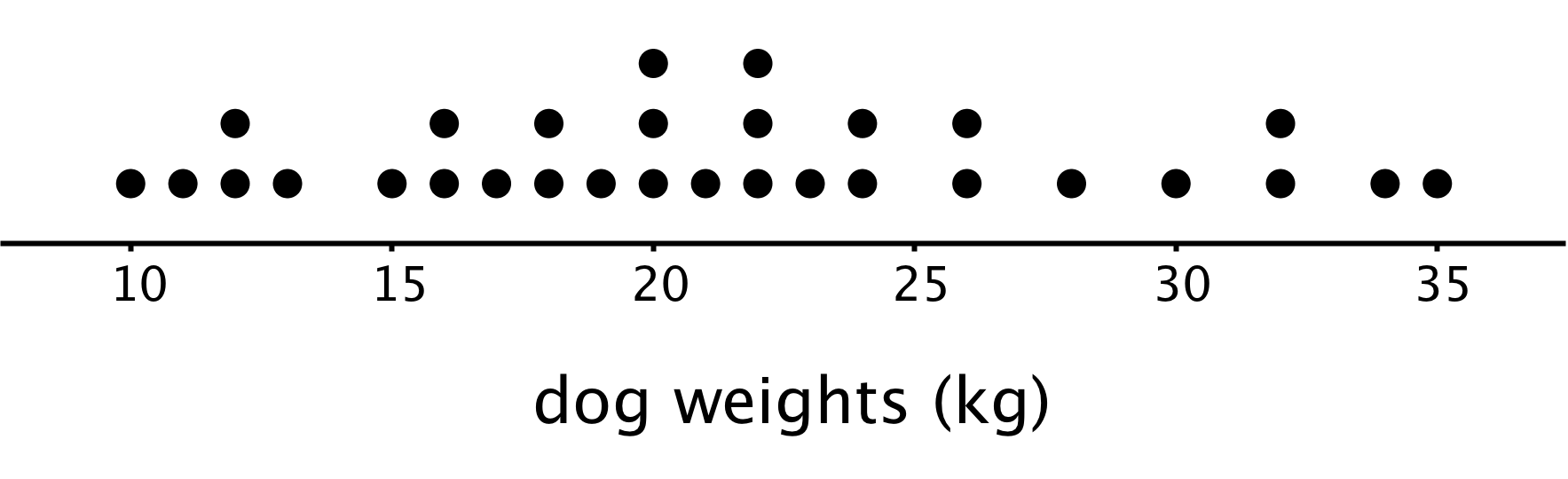
4.4: Cool-down - Family Size (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We often collect and analyze data because we are interested in learning what is “typical,” or what is common and can be expected in a group.
Sometimes it is easy to tell what a typical member of the group is. For example, we can say that a typical shape in this set is a large circle.

Just looking at the members of a group doesn’t always tell us what is typical, however. For example, if we are interested in the side length typical of squares in this set, it isn’t easy to do so just by studying the set visually.

In a situation like this, it is helpful to gather the side lengths of the squares in the set and look at their distribution, as shown in this dot plot.
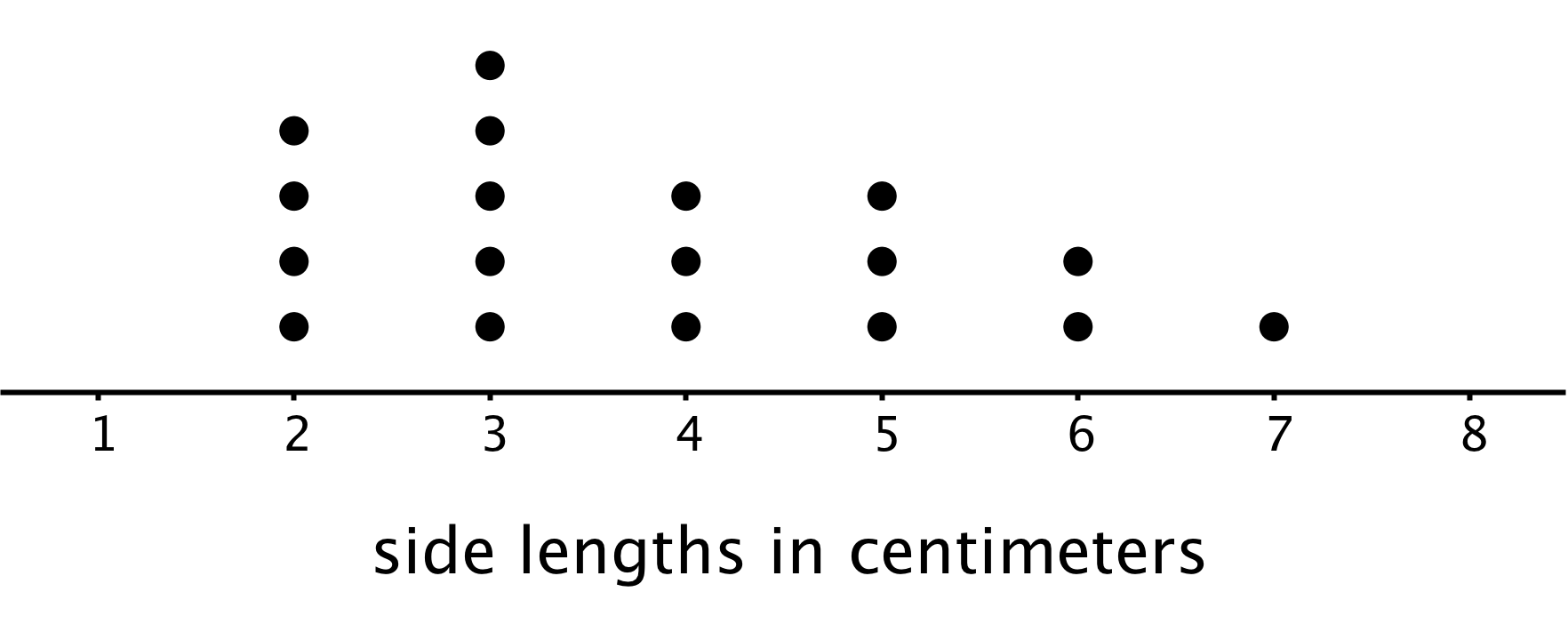
We can see that many of the data points are between 2 and 4, so we could say that side lengths between 2 and 4 centimeters or close to these lengths are typical of squares in this set.