Lesson 13
Median
Let's explore the median of a data set and what it tells us.
13.1: The Plot of the Story
-
Here are two dot plots and two stories. Match each story with a dot plot that could represent it. Be prepared to explain your reasoning.
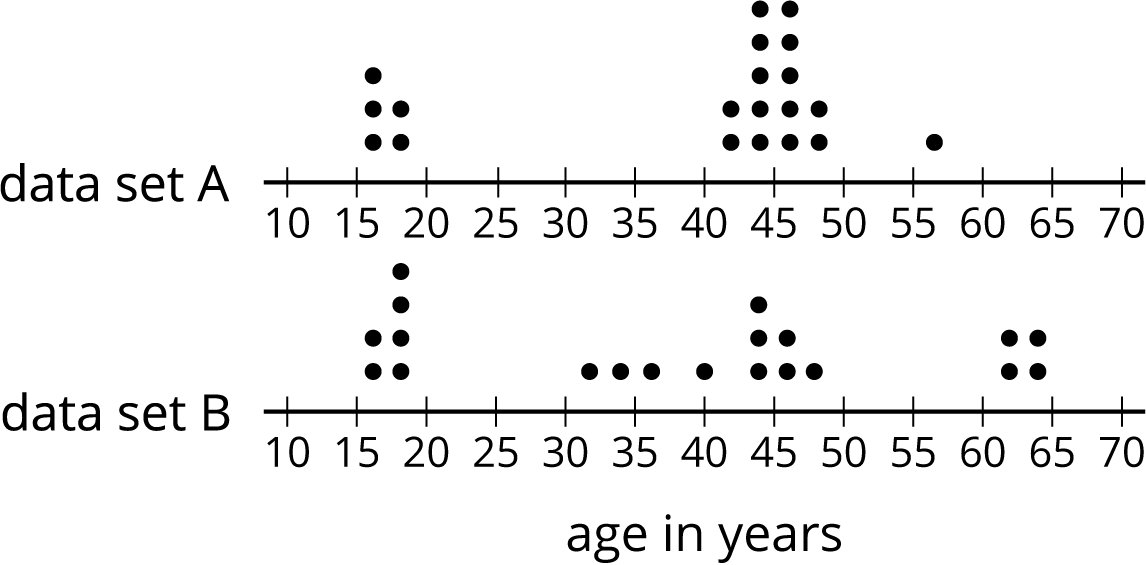
-
Twenty people—high school students, teachers, and invited guests—attended a rehearsal for a high school musical. The mean age was 38.5 years and the MAD was 16.5 years.
- High school soccer team practice is usually watched by supporters of the players. One evening, twenty people watched the team practice. The mean age was 38.5 years and the MAD was 12.7 years.
-
- Another evening, twenty people watched the soccer team practice. The mean age was similar to that from the first evening, but the MAD was greater (about 20 years).
Make a dot plot that could illustrate the distribution of ages in this story.
13.2: Siblings in the House
Here is data that shows the numbers of siblings of ten students in Tyler’s class.
1
0
2
1
7
0
2
0
1
10
- Represent the data shown with a dot plot.
-
Without making any calculations, estimate the center of the data based on your dot plot. What is a typical number of siblings for these sixth-grade students? Mark the location of that number on your dot plot.
- Find the mean. Show your reasoning.
-
- How does the mean compare to the value that you marked on the dot plot as a typical number of siblings? (Is it a little larger, a lot larger, exactly the same, a little smaller, or a lot smaller than your estimate?)
-
Do you think the mean summarizes the data set well? Explain your reasoning.
Invent a data set with a mean that is significantly lower than what you would consider a typical value for the data set.
13.3: Finding the Middle
-
Your teacher will give you an index card. Write your first and last names on the card. Then record the total number of letters in your name. After that, pause for additional instructions from your teacher.
-
Here is the data set on numbers of siblings from an earlier activity.
1
0
2
1
7
0
2
0
1
10
- Sort the data from least to greatest, and then find the median.
- In this situation, do you think the median is a good measure of a typical number of siblings for this group? Explain your reasoning.
-
Here is the dot plot showing the travel time, in minutes, of Elena’s bus rides to school.

- Find the median travel time. Be prepared to explain your reasoning.
- What does the median tell us in this context?
Summary
The median is another measure of center of a distribution. It is the middle value in a data set when values are listed in order. Half of the values in a data set are less than or equal to the median, and half of the values are greater than or equal to the median.
To find the median, we order the data values from least to greatest and find the number in the middle.
Suppose we have 5 dogs whose weights, in pounds, are shown in the table. The median weight for this group of dogs is 32 pounds because three dogs weigh less than or equal to 32 pounds and three dogs weigh greater than or equal to 32 pounds.
20
25
32
40
55
Now suppose we have 6 cats whose weights, in pounds, are as shown in the table. Notice that there are two values in the middle: 7 and 8.
4
6
7
8
10
10
The median weight must be between 7 and 8 pounds, because half of the cats weigh less or equal to 7 pounds and half of the cats weigh greater than or equal to 8 pounds.
In general, when we have an even number of values, we take the number exactly in between the two middle values. In this case, the median cat weight is 7.5 pounds because \((7+8)\div 2=7.5\).
Glossary Entries
- median
The median is one way to measure the center of a data set. It is the middle number when the data set is listed in order.
For the data set 7, 9, 12, 13, 14, the median is 12.
For the data set 3, 5, 6, 8, 11, 12, there are two numbers in the middle. The median is the average of these two numbers. \(6+8=14\) and \(14 \div 2 = 7\).