Lesson 8
Describing Distributions on Histograms
8.1: Which One Doesn’t Belong: Histograms (5 minutes)
Warm-up
This warm-up encourages students to make sense of histograms in terms of center and spread. It prompts students to hold mathematical conversations and explain their reasoning (MP3), and gives the teacher the opportunity to hear how students compare data sets represented by histograms.
Launch
Arrange students in groups of 2–4. Display the images for all to see. Give students 1 minute of quiet think time and ask them to indicate when they have noticed one image that does not belong and can explain why. When the minute is up, give students 2 minutes to share their thinking with their small group, and then, together, find a reason that each image doesn't belong.
Student Facing
Which histogram does not belong? Be prepared to explain your reasoning.
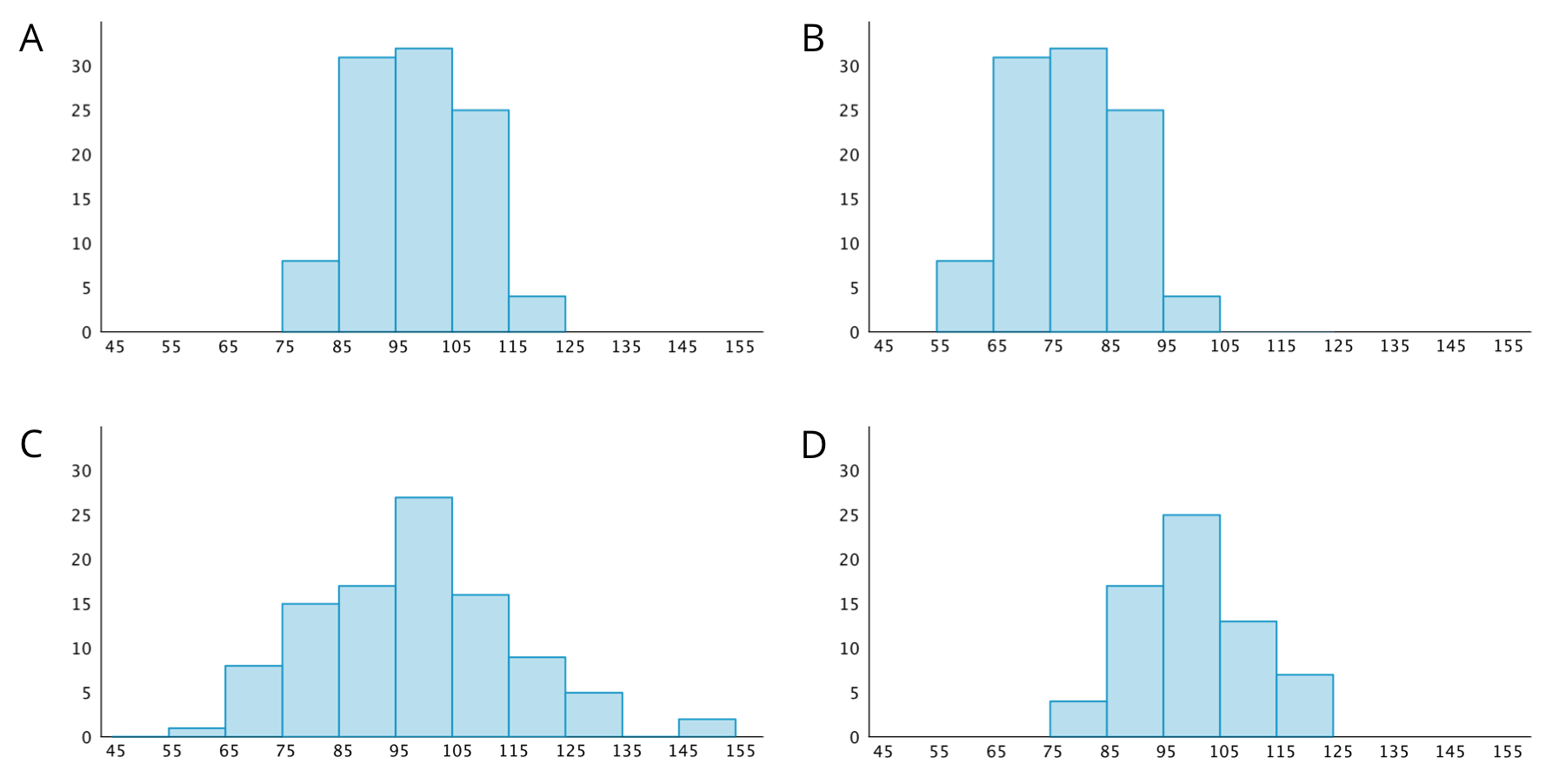
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share one reason their group decided a particular image does not belong. Record and display the responses for all to see. After each response, ask the class if they agree or disagree. Since there is no single correct answer to the question of which one does not belong, attend to students’ explanations and ensure the reasons given are reasonable.
If students use terms that are essential in this unit (such as center, spread, distribution, frequency, etc.), ask them to explain their meanings in their own words; these are opportunities to reinforce their understanding of the terms and to note any misconceptions. If students give unsubstantiated claims, ask them to substantiate them.
8.2: Sorting Histograms (20 minutes)
Activity
This activity is designed to expand both students’ exposure to various features of distributions and the language they could use to describe distributions. Students sort histograms based on features such as symmetry, gaps, clusters, and unusual values. In earlier grades, students used the term “symmetry” to describe geometric figures (4.G.3); here they use it to describe the shape of a distribution.
Launch
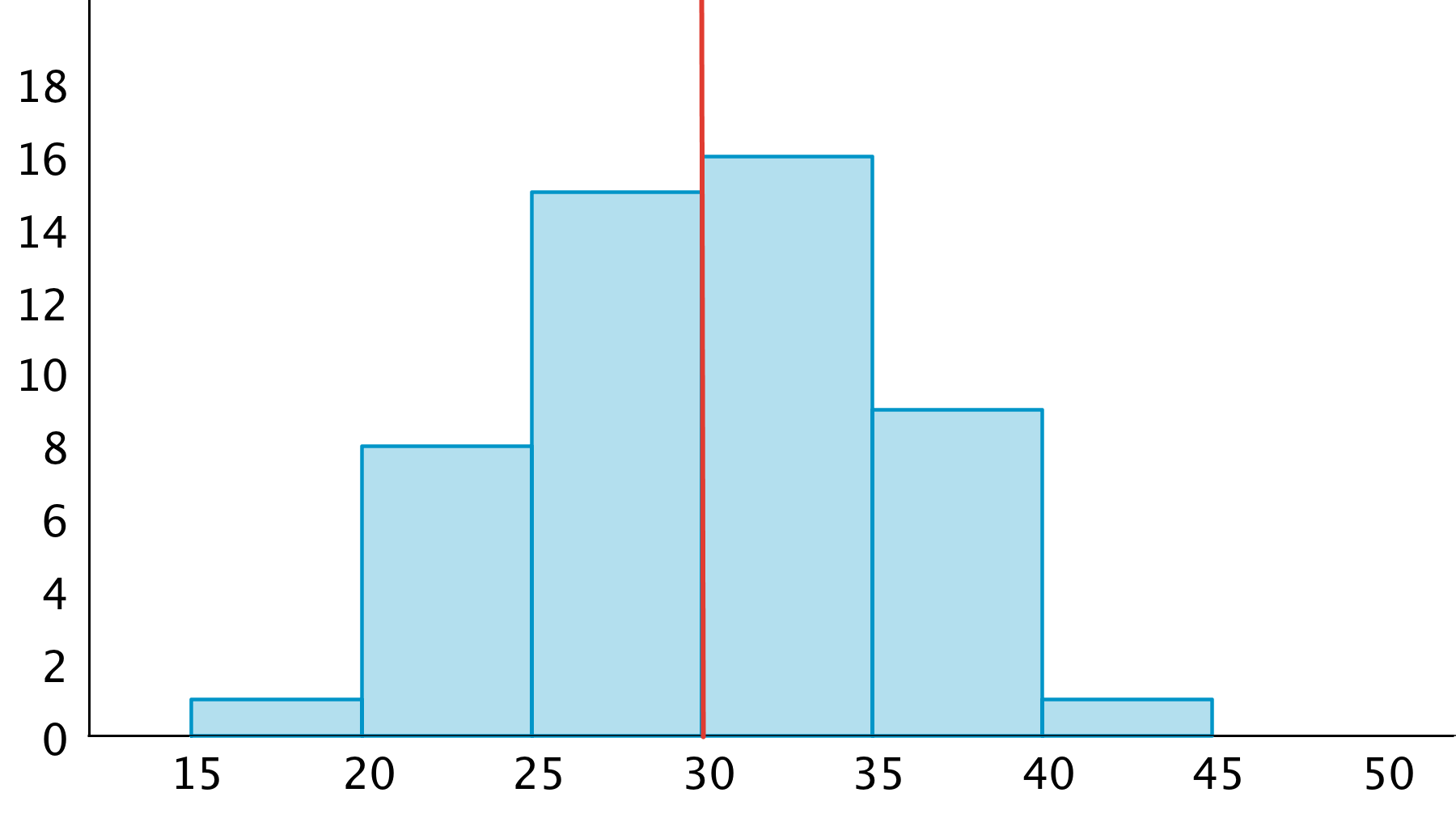
Display the image of the histogram here for all to see. Explain to students that a diagram of a distribution—a dot plot or a histogram—is described as symmetrical if you can draw a line on the diagram and the parts on one side of the line mirror the parts on the other side. Many distributions are not perfectly symmetrical, but are close to or approximately symmetrical.
The histogram here shows an approximately symmetrical distribution. When a line is drawn at the center (such as the line at 30) the two sides are roughly mirror images. If you were to fold the histogram at the line, the two sides would be close to matching.
Tell students that symmetry is used to describe distributions, and that they will now look for symmetry and other features of distributions in a dozen histograms.
Arrange students in groups of 3–4. Give each group one set of pre-cut cards from the blackline master. Ask students to study the histograms and identify the features described on their task statement. Give groups 10–12 minutes to complete the activity. Explain that each group will need to discuss their work with another group after the first question and before completing the rest of the activity.
Design Principle(s): Optimize output (for generalization); Cultivate conversation
Student Facing
- Your teacher will give your group a set of histogram cards. Sort them into two piles—one for histograms that are approximately symmetrical, and another for those that are not.
-
Discuss your sorting decisions with another group. Do both groups agree which cards should go in each pile? If not, discuss the reasons behind the differences and see if you can reach agreement. Record your final decisions.
-
Histograms that are approximately symmetrical:
-
Histograms that are not approximately symmetrical:
-
-
Histograms are also described by how many major peaks they have. Histogram A is an example of a distribution with a single peak that is not symmetrical.
Which other histograms have this feature?
-
Some histograms have a gap, a space between two bars where there are no data points. For example, if some students in a class have 7 or more siblings, but the rest of the students have 0, 1, or 2 siblings, the histogram for this data set would show gaps between the bars because no students have 3, 4, 5, or 6 siblings.
Which histograms do you think show one or more gaps?
-
Sometimes there are a few data points in a data set that are far from the center. Histogram A is an example of a distribution with this feature.
Which other histograms have this feature?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Students will have had a chance to discuss the different features of a distribution in small groups. Use the whole-class discussion to prompt students to think about what the features might mean, and whether or how they affect the way we characterize a distribution. Remind students that we have been using the center of a distribution to talk about what is typical in a group. Discuss some of these questions:
- “Look at the histograms that you think show symmetry. When a distribution is approximately symmetrical, where might its center be?”
- “Now look at the histograms that you think are not approximately symmetrical. Where might its center be? How might we describe what is typical of a group that has one peak that is not symmetrical (such as that in Histogram B)?”
- “Look at the histograms that show gaps. How might a gap (such as that in Histogram K) affect our description of what is typical in a group?”
- “Look at the histograms that have values that are far away from other values. Do unusual values (such as those in Histogram G) affect our description of center and spread? If those unusual values weren't there, would our description of center and spread change?”
Expect students’ answers to be very informal. The goal of the discussion is to raise students' awareness that the shape and features of distributions may affect how we characterize the data. This experience provides a conceptual foundation that would help students make sense of measures of center (mean and median) and measures of spread (mean absolute deviation, interquartile range, and range) later.
8.3: Getting to School (10 minutes)
Activity
In this activity, students draw a bar graph and histogram, then describe the distributions shown on each display. Although the two visual displays may appear similar at first glance, there are important distinctions between the representations. Students notice differences in how we might characterize distributions in bar graphs and those in histograms, including how we describe typical values or categories. Along the way, students consolidate their understanding about categorical and numerical data.
Launch
Students will need the data on their travel methods and times, collected at the beginning of the unit. Distribute or display the data collected for these questions from the survey given earlier in the unit. Alternatively, complete the tables in the blackline master ahead of time.
Arrange students in groups of 2. Give one copy of the blackline master to each group of students. Display the data from the prior survey or the completed frequency tables for all to see or give a copy to each group of 2 students. Give students 5–6 minutes to complete the activity. Ask one partner to create a bar graph to represent the data on the class’s travel methods and the other to create a histogram to represent the data on travel times, and then answer the questions together.
Student Facing
Your teacher will provide you with some data that your class collected the other day.
- Use the data to draw a histogram that shows your class’s travel times.

- Describe the distribution of travel times. Comment on the center and spread of the data, as well as the shape and features.
- Use the data on methods of travel to draw a bar graph. Include labels for the horizontal axis.

- Describe what you learned about your class’s methods of transportation to school. Comment on any patterns you noticed.
-
Compare the histogram and the bar graph that you drew. How are they the same? How are they different?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Use one of these suggestions (or make up your own). Research data to create a histogram. Then, describe the distribution.
- Heights of 30 athletes from multiple sports
- Heights of 30 athletes from the same sport
- High temperatures for each day of the last month in a city you would like to visit
- Prices for all the menu items at a local restaurant
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to recognize the differences between histograms and bar graphs.
Select one student to show a completed histogram and another to show a completed bar graph. Then, solicit several observations about how the two graphical displays compare. Ask questions such as:
- “How are the bar graphs and histograms alike? How are they different?”
- “Can we use a bar graph to display the data on travel times? Why or why not?”
- “Can we use a histogram to display the data on methods of travel? Why or why not?”
Next, select a few other students to share their descriptions of the distributions shown on each type of display. Then, ask questions such as:
- “How are your descriptions of the distribution for travel methods different than those for travel times?”
- “Can you talk about the shape of a distribution shown on a bar graph? Can you talk about its center and spread? Why or why not?”
Students should recognize that only the distribution of numerical data can be described in terms of shape, center, or spread. We cannot analyze these features for a distribution of a categorical data on a bar graph because a bar graph does not use a number line. This means the bars can be drawn anywhere, in any order, and with any kind of spacing, so shape, center, and spread would have no meaning.
Supports accessibility for: Language; Organization
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, we look at the shapes and features of distributions that are represented by histograms.
- “What does it mean for a histogram to have symmetry?”
- “What is a 'peak' in a distribution? Is it always in the middle, or can it be to one side?”
- “Can a distribution have more than one peak?”
- “What does it mean for a histogram to show a cluster (or more than one clusters)?”
- “What does it mean for a histogram to show a gap?”
We also contrast bar graphs and histograms.
- “When do we use a histogram and when do we use a bar graph?”
- “What are the major differences between how a histogram is drawn and how a bar graph is drawn?”
8.4: Cool-down - Point Spread (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can describe the shape and features of the distribution shown on a histogram. Here are two distributions with very different shapes and features.
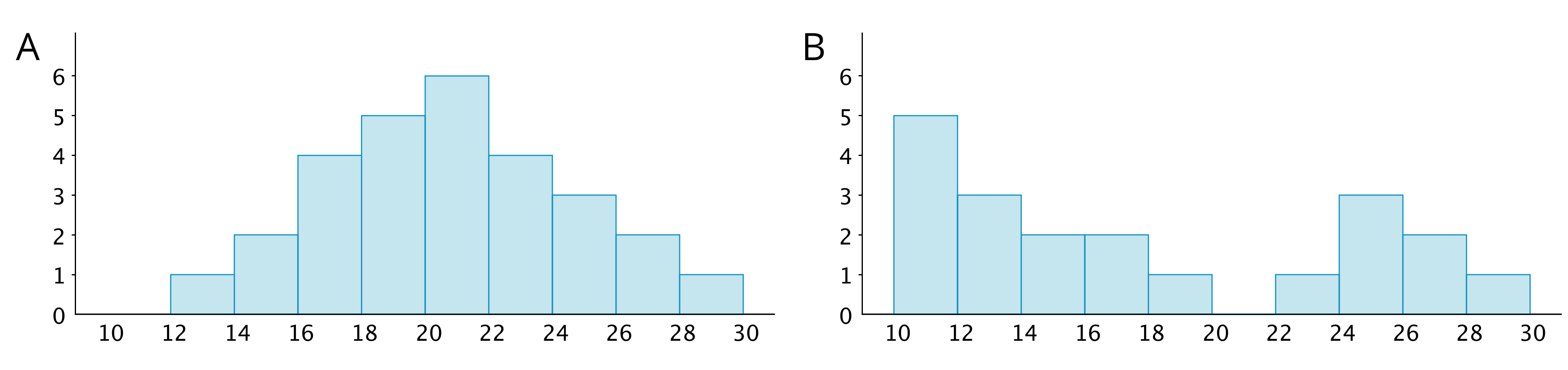
- Histogram A is very symmetrical and has a peak near 21. Histogram B is not symmetrical and has two peaks, one near 11 and one near 25.
- Histogram B has two clusters. A cluster forms when many data points are near a particular value (or a neighborhood of values) on a number line.
- Histogram B also has a gap between 20 and 22. A gap shows a location with no data values.
Here is a bar graph showing the breeds of 30 dogs and a histogram for their weights.
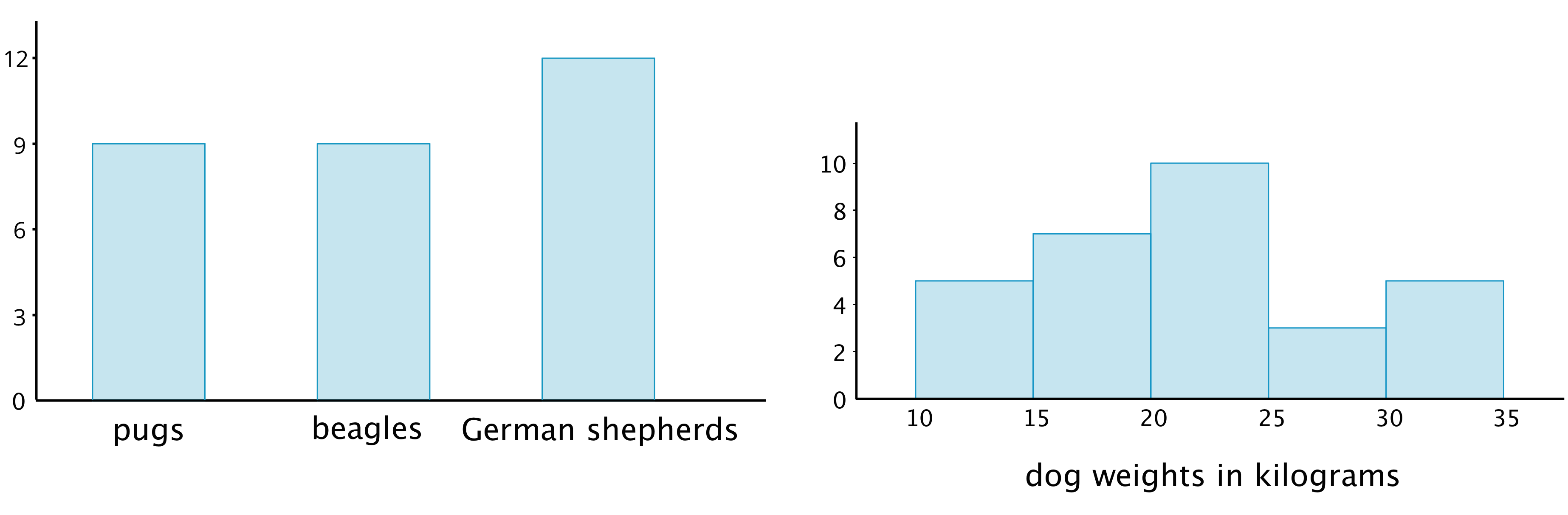
Bar graphs and histograms may seem alike, but they are very different.
- Bar graphs represent categorical data. Histograms represent numerical data.
- Bar graphs have spaces between the bars. Histograms show a space between bars only when no data values fall between the bars.
- Bars in a bar graph can be in any order. Histograms must be in numerical order.
- In a bar graph, the number of bars depends on the number of categories. In a histogram, we choose how many bars to use.