Lesson 11

Han recorded the number of pages that he read each day for five days. The dot plot shows his data.

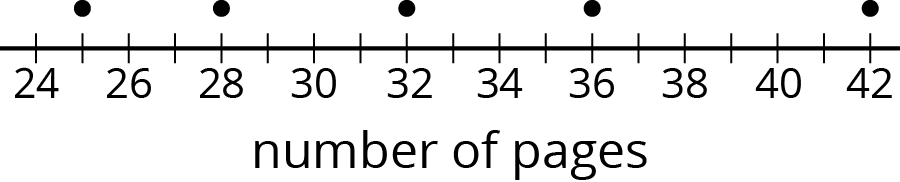
1. Is 30 pages a good estimate of the mean number of pages that Han read each day? Explain your reasoning.
2. Find the mean number of pages that Han read during the five days. Draw a triangle to mark the mean on the dot plot.
3. Use the dot plot and the mean to complete the table.

   number of pages	distance from mean	left or right of mean
   25		left
   28
   32
   36
   42

4. Calculate the mean absolute deviation (MAD) of the data. Explain or show your reasoning.

Ten sixth-grade students recorded the amounts of time each took to travel to school. The dot plot shows their travel times.

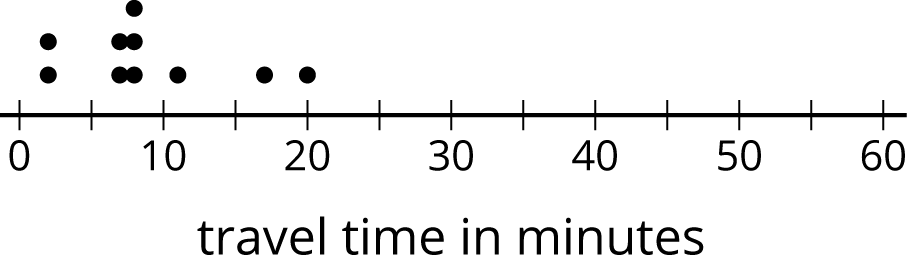
The mean travel time for these students is approximately 9 minutes. The MAD is approximately 4.2 minutes.​

1. Which number of minutes—9 or 4.2—is a typical amount of time for the ten sixth-grade students to travel to school? Explain your reasoning.
2. Based on the mean and MAD, Jada believes that travel times between 5 and 13 minutes are common for this group. Do you agree? Explain your reasoning.
3. A different group of ten sixth-grade students also recorded their travel times to school. Their mean travel time was also 9 minutes, but the MAD was about 7 minutes. What could the dot plot of this second data set be? Describe or draw how it might look.

In an archery competition, scores for each round are calculated by averaging the distance of 3 arrows from the center of the target.

An archer has a mean distance of 1.6 inches and a MAD distance of 1.3 inches in the first round. In the second round, the archer's arrows are farther from the center but are more consistent. What values for the mean and MAD would fit this description for the second round? Explain your reasoning.