Lesson 6

Estimating Probabilities Using Simulation

View Student Lesson

Lesson Narrative

This lesson introduces the idea of simulation. Different groups of students use different chance experiments that are designed to enable you to approximate the probability of a real world event.

Students follow a process similar to what they used in previous lessons for calculating relative frequencies (the activities in which students were rolling a 1 or 2 on a number cube or drawing a green block out of a bag). The distinction in this lesson is that the outcomes students are tracking are from an experiment designed to represent the outcome of some other experiment that would be harder to study directly. Students see that a simulation depends on the experiment used in the simulation being a reasonable stand-in for the actual experiment of interest (MP4).

This lesson works with estimating the probability of simple events in preparation for students being able to estimate the probability of compound events in upcoming lessons.


Learning Goals

Teacher Facing

  • Comprehend the that term “simulation” (in written and spoken language) refers to a chance experiment used to represent a real-world situation.
  • Describe (orally and in writing) a simple chance experiment that could be used to simulate a real-world event.
  • Perform a simulation, and use the results to estimate the probability of a simple event in a real-world situation (using words and other representations).

Student Facing

Let’s simulate real-world situations.

Required Materials

Required Preparation

Print and cut up slips and spinners from the Diego's Walk blackline master. Provide each group of 3 supplies for 1 type of simulation: choosing a situation slip from a bag, spinning a spinner, or rolling 2 number cubes.  The supplies for each simulation include:

  • a paper bag containing a set of slips cut from the blackline master
  • a spinner cut from the blackline master, a pencil and a paper clip
  • 2 standard number cubes

Learning Targets

Student Facing

  • I can simulate a real-world situation using a simple experiment that reflects the probability of the actual event.

CCSS Standards

Building On

Addressing

Glossary Entries

  • simulation

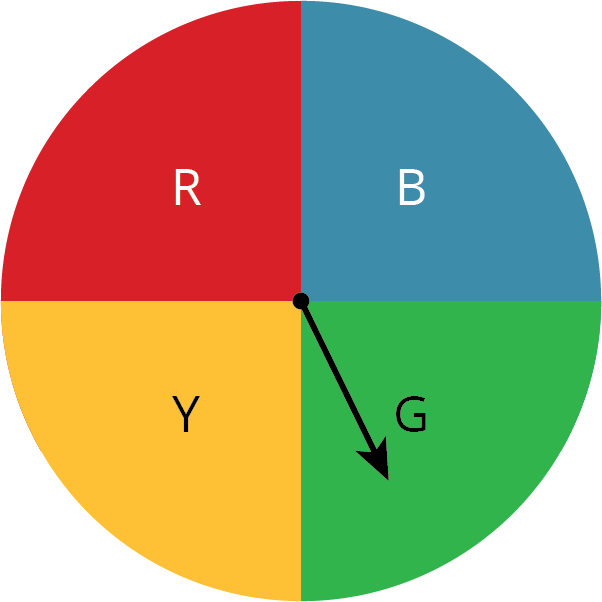
    A simulation is an experiment that is used to estimate the probability of a real-world event.

    For example, suppose the weather forecast says there is a 25% chance of rain. We can simulate this situation with a spinner with four equal sections. If the spinner stops on red, it represents rain. If the spinner stops on any other color, it represents no rain.

    A circular spinner divided into 4 equal parts. 

Print Formatted Materials

For access, consult one of our IM Certified Partners.

Additional Resources

Google Slides

For access, consult one of our IM Certified Partners.
PowerPoint Slides

For access, consult one of our IM Certified Partners.