Lesson 16
Estimating Population Proportions
16.1: Getting to School (5 minutes)
Warm-up
The purpose of this warm-up is for students to compute the fraction of individuals whose responses fall in a specified category. This activity gives students time to think about how to compute these fractions from categorical data.
For the second and third questions, students may debate whether to include the 10 minute times or not. According to the wording of the question asked, it does ask for more than 10 minute times, so maybe exactly 10 minutes should not count (since \(10 \ngtr 10\)). On the other hand, all of the values are listed as whole numbers, so a student who takes 10 minutes and 1 second to get to school may have rounded down to 10, but should have been counted. Noticing the large difference in answers for the third question, it may be worth clarifying the data in this instance, even for an estimate.
Monitor for students who include the 10 minute times for the second and third questions as well as those who do not.
Launch
Give students 2 minutes of quiet work time followed by a whole-class discussion.
Student Facing
A teacher asked all the students in one class how many minutes it takes them to get to school. Here is a list of their responses:
- 20
- 10
- 15
- 8
- 5
- 15
- 10
- 5
- 20
- 5
- 15
- 10
- 3
- 10
- 18
- 5
- 25
- 5
- 5
- 12
- 10
- 30
- 5
- 10
-
What fraction of the students in this class say:
- it takes them 5 minutes to get to school?
- it takes them more than 10 minutes to get to school?
-
If the whole school has 720 students, can you use this data to estimate how many of them would say that it takes them more than 10 minutes to get to school?
Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to share their methods for computing the solutions. Include previously identified students who did or did not include the 10 minute values in their calculations.
If it does not arise during the discussion, explain that answering the third question with the data at hand is only accurate if the sample data is representative of the school. It is possible that the class happens to contain only students who get a ride to school, but much of the school rides the bus.
16.2: Reaction Times (15 minutes)
Activity
In previous lessons, students examined the estimation of the mean and median for populations using data from a sample. In this activity, students apply similar reasoning to estimating the proportion of a population that matches certain characteristics. Students collect a sample of 20 reaction times and compute the fraction of responses in their sample that are in a given range. Then, in the discussion, students compare their estimations to the known population proportion and use the class's proportions to gauge the accuracy of their estimate (MP6).
Launch
Arrange students in groups of 2. Distribute bags of slips cut from the blackline master.
Tell students that, in statistics, a proportion is a number between 0 and 1 that represents the fraction of the data that fits into the desired category. For example, with the data: {Yes, Yes, Yes, No, Maybe} the proportion of “Yes” answers is \(\frac{3}{5}\) or 0.6.
Introduce the context: All 120 seniors at a high school were asked to click a button as soon as they noticed a box change color and the response time was recorded in seconds. These 120 response times represent the population for this activity. Their responses are written on the slips of paper in the bag.
When selecting a sample of 20, each value does not need to be replaced before taking the next one.
Allow students 10 minutes of partner work time followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
The track coach at a high school needs a student whose reaction time is less than 0.4 seconds to help out at track meets. All the twelfth graders in the school measured their reaction times. Your teacher will give you a bag of papers that list their results.
- Work with your partner to select a random sample of 20 reaction times, and record them in the table.
- What proportion of your sample is less than 0.4 seconds?
- Estimate the proportion of all twelfth graders at this school who have a reaction time of less than 0.4 seconds. Explain your reasoning.
- There are 120 twelfth graders at this school. Estimate how many of them have a reaction time of less than 0.4 seconds.
-
Suppose another group in your class comes up with a different estimate than yours for the previous question.
-
What is another estimate that would be reasonable?
-
What is an estimate you would consider unreasonable?
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The reason a proportion is between 0 and 1 is because we are specifically looking for the proportion of a desired category out of the whole group. This is a “part out of whole” fraction, which will be a number between 0 and 1.
Activity Synthesis
The purpose of the discussion is for students to see how multiple sample proportions can help revise their estimates and give an idea of how accurate the individual estimates from samples might be.
Ask the groups to share the proportion from their sample that had fast reaction times and display the results for all to see.
Some questions for discussion:
- “Using the class’s data, how accurate do you think your group's estimate is? Explain or show your reasoning.” (Students should mention the variability of the proportions from the samples influencing the accuracy of the estimate.)
- “The actual proportion for this population is 0.5. How close was your estimate? Explain why your estimate was not exactly the same.” (Each sample might be slightly different since they do not include all of the values, but they should be close.)
- “If each group had 40 reaction times in their samples instead of 20, do you think the estimate would be more or less accurate?” (The estimate should be more accurate since there is more information available.)
Design Principle(s): Optimize output (for comparison); Cultivate conversation
16.3: A New Comic Book Hero (15 minutes)
Activity
In the previous activity, students collected their own sample and computed an estimate for the population proportion based on the sample. In this activity, students use a different context to practice exploring proportions from samples and their extension to populations. The optional activity following this one continues with this context exploring sampling variability.
Launch
Keep students in groups of 2.
Tell students that three comic books, The Adventures of Super Sam, Beyond Human, and Mysterious Planets, are all planning to add a new superhero to their stories. A survey was sent to dedicated readers of each series to ask what type of ability the new hero should have: fly, freeze, or another power.
Display the tables from the Task Statement for all to see. Ask students, “What do you notice? What do you wonder?”
Students may notice:
- There are 4 different responses: fly, freeze, super strength, and invisibility.
- The number of responses for each of the 4 different responses.
- There are 20 responses.
Students may wonder:
- Will the decision for the new hero's power be based only on this survey?
- What proportion chose each of the different powers?
- Is this sample of 20 responses representative of the population?
Give students 5–7 minutes of partner work time followed by a whole-class discussion.
Supports accessibility for: Visual-spatial processing
Student Facing
Here are the results of a survey of 20 people who read The Adventures of Super Sam regarding what special ability they think the new hero should have.

| response | what new ability? |
|---|---|
| 1 | fly |
| 2 | freeze |
| 3 | freeze |
| 4 | fly |
| 5 | fly |
| 6 | freeze |
| 7 | fly |
| 8 | super strength |
| 9 | freeze |
| 10 | fly |
| response | what new ability? |
|---|---|
| 11 | freeze |
| 12 | freeze |
| 13 | fly |
| 14 | invisibility |
| 15 | freeze |
| 16 | fly |
| 17 | freeze |
| 18 | fly |
| 19 | super strength |
| 20 | freeze |
- What proportion of this sample want the new hero to have the ability to fly?
-
If there are 2,024 dedicated readers of The Adventures of Super Sam, estimate the number of readers who want the new hero to fly.
Two other comic books did a similar survey of their readers.
- In a survey of people who read Beyond Human, 42 out of 60 people want a new hero to be able to fly.
- In a survey of people who read Mysterious Planets, 14 out of 40 people want a new hero to be able to fly.
- Do you think the proportion of all readers who want a new hero that can fly are nearly the same for the three different comic books? Explain your reasoning.
-
If you were in charge of these three comics, would you give the ability to fly to any of the new heroes? Explain your reasoning using the proportions you calculated.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to recognize the value of a proportion and why a sample may be necessary to estimate the proportion for the population.
Some questions for discussion:
- “Explain why you think a sample was used instead of the population for this situation.” (The population is too large to ask all of the readers about their preference. Also, the authors may want the power of the new hero to be a surprise to some readers, so they want to get some information without telling everyone about what is coming.)
- “Based on the proportions computed in each of these samples, would you suggest to the authors of any of the comic books to give their new hero the ability to fly?”
- “Although the proportion of responses from the Mysterious Planets sample who chose flight was only 0.35, it was the most popular choice (freeze, super strength, invisibility, and other powers split the remaining votes). Does this information change your answer to the previous question?”
- “Of the three estimates, which do you think is most accurate? Explain your reasoning.” (Beyond Human has the largest sample, so it may be the most accurate.)
Design Principle(s): Optimize output (for explanation)
16.4: Flying to the Shelves (10 minutes)
Optional activity
This optional activity goes beyond grade-level expectations to deepen students’ understanding of sampling variability.
This activity continues the comic book context introduced in the previous activity. There is not a measure of variability such as MAD or IQR for proportions since the data are categorical rather than quantitative, so other methods must be employed to determine the accuracy of an estimate. Students look at dot plots showing the results from multiple samples to gauge the accuracy of the estimates for population proportions (MP7). This activity will provide a foundation for work in later grades.
Launch
Arrange students in groups of 2.
Help students make sense of the dot plot. Each dot in the dot plot represents the proportion from a random sample of 20 readers. 50 random samples were taken and the 50 proportions are plotted on the dot plot. For example, the 0.4 proportion from the previous activity would be represented by one of the 4 dots at 0.4 on the first dot plot.
Ask, “Are any of the sample proportions greater than or equal to 0.5? What does this mean?” (Yes, 2 dots are greater than or equal to 0.5. This means that, in those samples, at least half of the people prefer the new hero to have the ability to fly.)
Give students 5–7 minutes of partner work time followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
The authors of The Adventures of Super Sam chose 50 different random samples of readers. Each sample was of size 20. They looked at the sample proportions who prefer the new hero to fly.
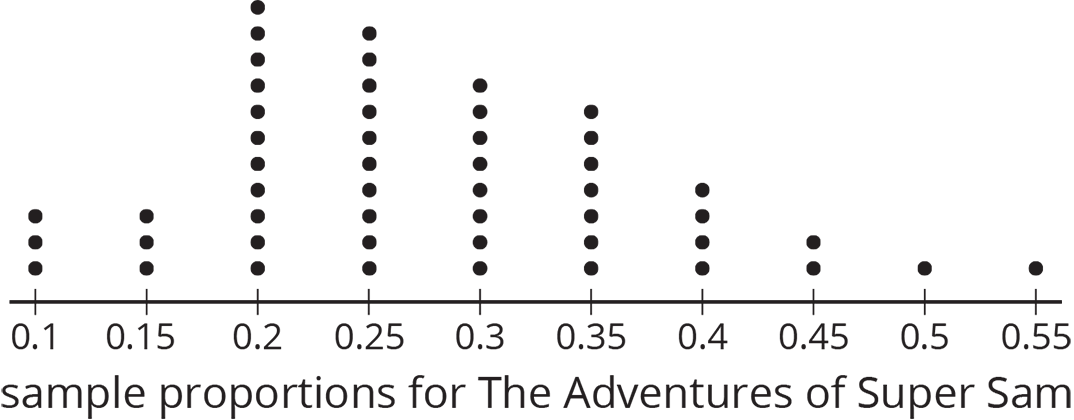
- What is a good estimate of the proportion of all readers who want the new hero to be able to fly?
- Are most of the sample proportions within 0.1 of your estimate for the population proportion?
-
If the authors of The Adventures of Super Sam give the new hero the ability to fly, will that please most of the readers? Explain your reasoning.
The authors of the other comic book series created similar dot plots.


-
For each of these series, estimate the proportion of all readers who want the new hero to fly.
- Beyond Human:
- Mysterious Planets:
- Should the authors of either of these series give their new hero the ability to fly?
- Why might it be more difficult for the authors of Mysterious Planets to make the decision than the authors of the other series?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Draw an example of a dot plot with at least 20 dots that represent the sample proportions for different random samples that would indicate that the population proportion is above 0.6, but there is a lot of uncertainty about that estimate.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to talk about how the variability in sample proportions affects their trust in the estimates of the population proportion.
Consider these questions for discussion:
- “When estimating a population mean or median from a random sample, measures of variability from a sample can be used to help gauge the accuracy of the estimate. With proportions there is not a measure of variability in the same way. How did the information in this activity guide your thoughts about the accuracy of the population estimate?” (Many samples were taken and their proportions computed. The variability of these sample proportions showed how much to trust the population estimate.)
- “How does the distribution of values in the dot plots of sample proportions affect your trust in an estimate of population proportion?” (The more variability, the less certainty in the estimate.)
- “How would the distributions change if the number of responses in each sample were increased?” (The center should remain about the same, the variability should decrease or, in other words, the dots in the dot plot should get closer together towards the center.)
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
Consider asking these discussion questions to clarify the main ideas of the lesson:
- “When using data, what is a proportion? How is it calculated?” (A proportion is the fraction of the data that are in a certain category. It is calculated by counting the number of data values in the category and dividing by the total number of data values in the sample.)
- “In order to say that more than half of the people in a sample responded with a certain answer, what would the proportion for that answer be?” (Any value greater than 0.5)
- “A random sample indicates that a 0.45 proportion of people shopping at a certain store prefer wheat bread to white bread. The store has 3,000 customers. Estimate the number of people shopping at the store who prefer wheat bread.” (About 1,350 since \(0.45 \boldcdot 3,\!000 = 1,\!350\))
16.5: Cool-down - More than 48 Grams (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes a data set consists of information that fits into specific categories. For example, we could survey students about whether they have a pet cat or dog. The categories for these data would be {neither, dog only, cat only, both}. Suppose we surveyed 10 students. Here is a table showing possible results:
| option | number of responses |
|---|---|
| neither dog nor cat | 2 |
| dog only | 4 |
| cat only | 1 |
| both dog and cat | 3 |
In this sample, 3 of the students said they have both a dog and a cat. We can say that the proportion of these students who have a both a dog and a cat is \(\frac{3}{10}\) or 0.3. If this sample is representative of all 720 students at the school, we can predict that about \(\frac{3}{10}\) of 720, or about 216 students at the school have both a dog and a cat.
In general, a proportion is a number from 0 to 1 that represents the fraction of the data that belongs to a given category.