Lesson 9
Multi-step Experiments
9.1: True or False? (5 minutes)
Warm-up
The purpose of this warm-up is to gather strategies and understandings students have for averaging numbers. Understanding these strategies will help students develop fluency and will be useful later in this unit when students will need to be able to compute averages of values.
While 3 problems are given, it may not be possible to share every strategy for all the problems. Consider gathering only 2 or 3 different strategies per problem, saving most of the time for the final question.
Launch
Reveal one problem at a time. Give students 30 seconds of quiet think time for each problem and ask them to give a signal when they have an answer and a strategy. Keep all previous problems displayed throughout the talk. Follow with a whole-class discussion.
Student Facing
Is each equation true or false? Explain your reasoning.
\(8=(8+8+8+8)\div3\)
\((10+10+10+10+10)\div5=10\)
\((6+4+6+4+6+4)\div6=5\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. To involve more students in the conversation, consider asking:
-
“Who can restate ___’s reasoning in a different way?”
-
“Did anyone have the same strategy but would explain it differently?”
-
“Did anyone solve the problem in a different way?”
-
“Does anyone want to add on to _____’s strategy?”
-
“Do you agree or disagree? Why?”
9.2: Spinning a Color and Number (10 minutes)
Activity
In this activity, students are reminded how to calculate probability based on the number of outcomes in the sample space, then apply that to multi-step experiments. The events are described in everyday language, so students need to reason abstractly (MP2) to identify the outcomes described. This lesson begins with students returning to a problem they have previously seen when writing out the sample space. This will save students some time if they can recall or refer back to the initial problem. In the following activities, students will work with situations for which they have not written out the sample space to practice finding probabilities using all the necessary steps.
Launch
Arrange students in groups of 2.
Display the two spinners for all to see. Ask students, “What do you notice? What do you wonder?”
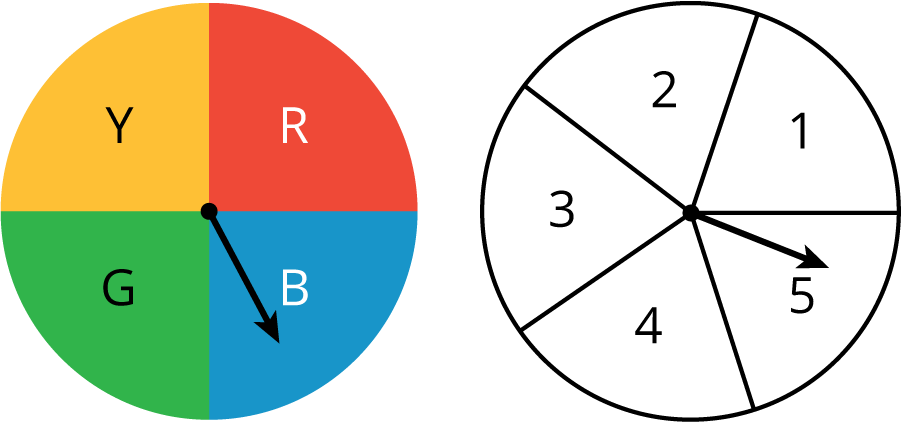
Give students 1 minute to think about the image. Record their responses for all to see.
Students may notice:
- The number of sections in each spinner.
- The labels for the two spinners.
- Within each spinner, the sections are equally sized.
Students may wonder:
- Do you choose which one to spin or do you spin both?
- If you spin both, how many different outcomes will there be?
- Is this part of a game? If so, what is a “good” spin?
Tell students: “For sample spaces where each outcome is equally likely, recall that the probability of an event can be computed by counting the number of outcomes in the event and dividing that number by the total number of outcomes in the sample space.” For example, in the previous lesson, students found that there were 12 possible outcomes when flipping a coin and rolling a number cube. If we wanted the probability of getting heads and rolling an even number, we count that there are 3 ways to do this (H2, H4, and H6) out of the 12 outcomes in the sample space. So, the probability of getting heads and an even number should be \(\frac{3}{12}\) or \(\frac{1}{4}\) or 0.25.
Remind students that they have already drawn out the sample space for this chance experiment in a previous activity, and they may use that to help answer the questions.
Give students of 5 minutes quiet work time followed by partner and whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
The other day, you wrote the sample space for spinning each of these spinners once.
What is the probability of getting:
- Green and 3?
- Blue and any odd number?
- Any color other than red and any number other than 2?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to explain their interpretations of the questions and share methods for solving.
Some questions for discussion:
- “How did you calculate the number of outcomes in the sample space?” (Counting the items in the tree, table, or list, or using the multiplication idea from an earlier lesson.)
- “Although we had the sample space for this situation in a previous problem, how could you find the sample space if you did not know it already?” (Draw a tree, table, or list.)
- “For each problem, how many outcomes were in the event that was described? How did you count them?”
Design Principle(s): Support sense-making; Maximize meta-awareness
9.3: Cubes and Coins (20 minutes)
Activity
In this activity, students continue to compute probabilities for multi-step experiments using the number of outcomes in the sample space. The first problem involves a situation for which students have already seen the sample space. Following this problem, the class will discuss the merits of the different representations for writing out the sample space. The next two problems involve situations in which students may need to write out the sample space on their own. Students are also reminded that some events have a probability of 0, which represents an event that is impossible. In the discussion following the activity, students are asked to think about the probabilities of two events that make up the entire sample space and have no outcomes common to both events (MP2).
Launch
Keep students in groups of 2.
Assign each group a representation for writing out the sample space: a tree, a table, or a list. Tell students that they should write out the sample space for the first problem using the representation they were assigned. (This was done for them in a previous lesson and they are allowed to use those as a guide if they wish.)
Tell students that they should work on the first problem only and then pause for a discussion before proceeding to the next problems.
Give students 2 minutes of partner work time for the first problem followed by a pause for a whole-class discussion centered around the different representations for sample space.
After all groups have completed the first question, select at least one group for each representation and have them explain how they arrived at their answer. As the groups explain, display the appropriate representations for all to see. Ask each of the groups how they counted the number of outcomes in the sample space as well as the number of outcomes in the event using their representation.
List:
Heads 1, heads 2, heads 3, heads 4, heads 5, heads 6, tails 1, tails 2, tails 3, tails 4, tails 5, tails 6
Table:
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | H5 | H6 |
| T1 | T2 | T3 | T4 | T5 | T6 |
Tree:
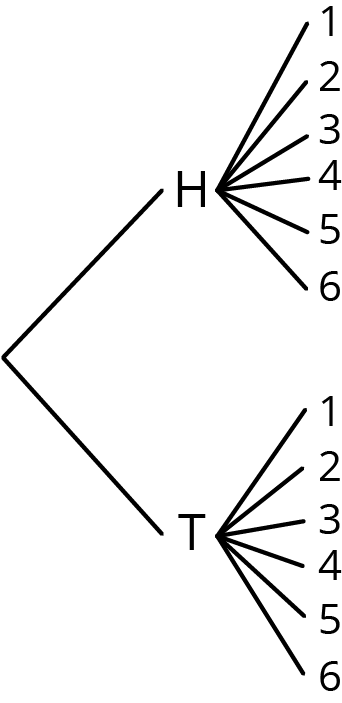
After students have had a chance to explain how they used the representations, ask students to give some pros and cons for using each of the representations. For example, the list method may be easy to write out and interpret, but could be very long and is not the easiest method for keeping track of which outcomes have been written and which still need to be included.
Allow the groups to continue with the remaining problems, telling them they may use any method they choose to work with the sample space for these problems. Give students 10 minutes of partner work time followed by a whole-class discussion about the activity as a whole.
Student Facing
The other day you looked at a list, a table, and a tree that showed the sample space for rolling a number cube and flipping a coin.
-
Your teacher will assign you one of these three structures to use to answer these questions. Be prepared to explain your reasoning.
- What is the probability of getting tails and a 6?
-
What is the probability of getting heads and an odd number?
Pause here so your teacher can review your work.
-
Suppose you roll two number cubes. What is the probability of getting:
- Both cubes showing the same number?
- Exactly one cube showing an even number?
- At least one cube showing an even number?
- Two values that have a sum of 8?
- Two values that have a sum of 13?
- Jada flips three quarters. What is the probability that all three will land showing the same side?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not recognize that rolling a 2 then a 3 is different from rolling a 3 then a 2. Ask students to imagine the number cubes are different colors to help see that there are actually 2 different ways to get these results.
Similarly, some students may think that HHT counts the same as HTH and THH. Ask the student to think about the coins being flipped one at a time rather than all tossed at once. Drawing an entire tree and seeing all the branches may further help.
Activity Synthesis
The purpose of the discussion is for students to explain their methods for solving the problems and to discuss how writing out the sample space aided in their solutions.
Poll the class on how they computed the number of outcomes in the sample space and the number of outcomes in the event for the second set of questions given these options: List, Table, Tree, Computed Outcomes Without Writing Them All Out, Another Method.
Consider these questions for discussion:
- “Which representation did you use for each of the problems?”
- “Do you think you will always try to use the same representation, or can you think of situations when one representation might be better than another?”
- “Did you have a method for finding the number of outcomes in the sample space or event that was more efficient than just counting them?” (The number of outcomes in the sample space for the number cubes could be found using \(6 \boldsymbol{\cdot} 6 = 36\). To find the number of outcomes with at least 1 even number, I knew there would be 6 for each time an even was rolled first and only 3 for each time an odd number was rolled first, so I found the number of outcomes by \(3 \boldsymbol{\cdot} 6 + 3 \boldsymbol{\cdot} 3 = 27\).)
- “One of the events had a probability of zero. What does this mean?”
(It is impossible.) - “What would be the probability of an event that was certain?” (1)
- “Jada was concerned with having all the coins show the same side. What would be the probability of having at least 1 coin not match the others?” (\(\frac{6}{8}\), since there are 6 outcomes where at least 1 coin does not match: HHT, TTH, HTH, THT, HTT, THH.)
- “How do the answers to Jada’s question and the one we just answered relate to one another?” (Since every outcome in the sample space has either “at least one heads” or “all tails,” and there is no outcome that applies to both events, together the sum of their probabilities must be 100% or 1.)
Design Principle(s): Support sense-making
9.4: Pick a Card (15 minutes)
Optional activity
The activity provides further practice in finding probabilities of events.
In this activity, students see an experiment that has two steps where the result of the first step influences the possibilities for the second step. Often this process is referred to as doing something “without replacement.” At this stage, students should approach these experiments in a very similar way to all of the other probability questions they have encountered, but they must be very careful about the number of outcomes in the sample space (MP6).
Launch
Keep students in groups of 2. Give students 5–7 minutes of quiet work time followed by partner and whole-class discussion.
Identify students who are not noticing that it is impossible to draw the same color twice based on the instructions. Refocus these students by asking them to imagine drawing a red card on the first pick and thinking about what’s possible to get for the second card.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Design Principle(s): Optimize output; Maximize meta-awareness
Student Facing
Imagine there are 5 cards. They are colored red, yellow, green, white, and black. You mix up the cards and select one of them without looking. Then, without putting that card back, you mix up the remaining cards and select another one.
-
Write the sample space and tell how many possible outcomes there are.
-
What structure did you use to write all of the outcomes (list, table, tree, something else)? Explain why you chose that structure.
-
What is the probability that:
-
You get a white card and a red card (in either order)?
-
You get a black card (either time)?
-
You do not get a black card (either time)?
-
You get a blue card?
-
You get 2 cards of the same color?
-
You get 2 cards of different colors?
-
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
In a game using five cards numbered 1, 2, 3, 4, and 5, you take two cards and add the values together. If the sum is 8, you win. Would you rather pick a card and put it back before picking the second card, or keep the card in your hand while you pick the second card? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may misread the problem and think that they replace the card before picking the next one. Ask these students to read the problem more carefully and ask the student, “What is possible to get when you draw the second card while you already have a red card in your hand?”
Activity Synthesis
The purpose of the discussion is for students to compare the same context with replacement and without replacement.
Consider asking these questions for discussion:
- “What would change about your calculations if the experiment required replacing the first card before picking a second card?” (There would be 25 outcomes in the sample space. The probability of getting the same color twice would be \(\frac{5}{25}\). The probability of getting different colors would be \(\frac{20}{25}\). The probability of getting red and white would be \(\frac{2}{25}\). The probability of getting a black card would be \(\frac{9}{25}\) and not getting a black card would be \(\frac{16}{25}\). It would still be impossible to get a blue card, so its probability would be 0.)
- “What do you notice about the sum of the probability of getting a black card and the probability of not getting a black card?” (They have a sum of 1.)
- “Explain why these outcomes might have probabilities with this relationship.” (Since you either get a black card or not, together their probabilities should be 1 or 100%.)
Lesson Synthesis
Lesson Synthesis
These discussion questions will help students reflect on their learning:
- “When the outcomes in the sample space are equally likely, how is the size of the sample space used to calculate the probability of an event?”
- “Now that you’ve have plenty of practice, do you have a favorite method for writing out the sample space?”
- “Are there times that one strategy for writing out the sample space makes more sense than others?”
9.5: Cool-down - A Number Cube and 10 Cards (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Suppose we have two bags. One contains 1 star block and 4 moon blocks. The other contains 3 star blocks and 1 moon block.
If we select one block at random from each, what is the probability that we will get two star blocks or two moon blocks?
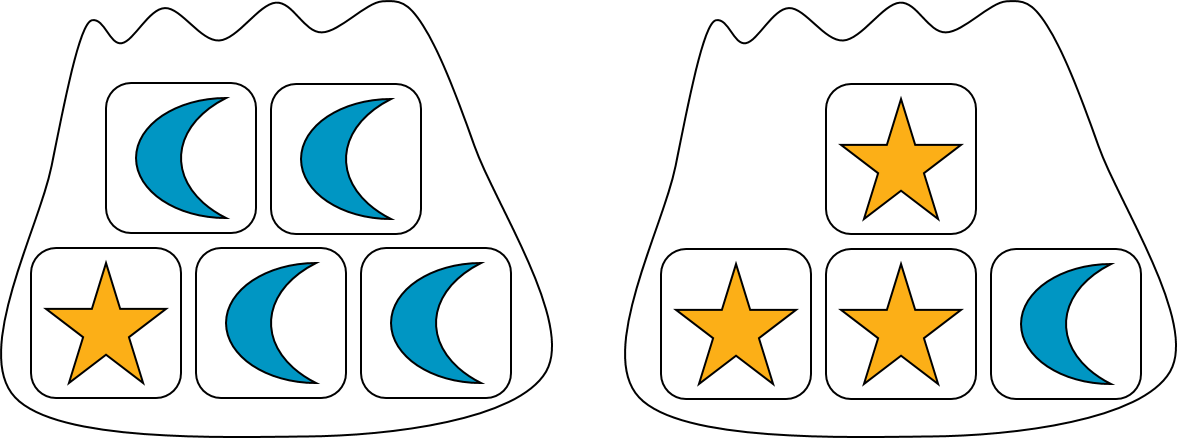
To answer this question, we can draw a tree diagram to see all of the possible outcomes.

There are \(5 \boldcdot 4 = 20\) possible outcomes. Of these, 3 of them are both stars, and 4 are both moons. So the probability of getting 2 star blocks or 2 moon blocks is \(\frac{7}{20}\).
In general, if all outcomes in an experiment are equally likely, then the probability of an event is the fraction of outcomes in the sample space for which the event occurs.