Lesson 5
More Estimating Probabilities
5.1: Is it Likely? (5 minutes)
Warm-up
The purpose of this warm-up is for students to think more deeply about probabilities and what the values actually represent. In this activity, students are asked to compare the likelihood of three events with probabilities given in different formats. In the discussion, students are also asked to think about the context of the situations to see that probabilities are not the only consideration when planning a response.
Launch
Give students 2 minutes of quiet work time followed by a whole-class discussion.
Student Facing
- If the weather forecast calls for a 20% chance of light rain tomorrow, would you say that it is likely to rain tomorrow?
- If the probability of a tornado today is \(\frac{1}{10}\), would you say that there will likely be a tornado today?
- If the probability of snow this week is 0.85, would you say that it is likely to snow this week?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students, "Which situation would you worry about the most? Is that the same situation that is the most likely?"
Note that our interpretation of the scenario influences how we feel about how likely an event is to happen. Although the likelihood of rain is higher, the implications of a tornado are much greater, so you may be more likely to worry about the tornado than the rain.
5.2: Making My Head Spin (20 minutes)
Activity
In this activity, students return to calculating probabilities using the sample space, and they compare the calculated probabilities to the outcomes of their actual trials. Students have a chance to construct arguments (MP3) about why probability estimates based on carrying out the experiment many times might differ from the expected probability. Students use a spinner in this activity, which will be helpful when designing simulations in upcoming lessons.
Launch
Arrange students in groups of 4.
Classes using the digital curriculum have spinner applets to use if they choose to. These applets are based on the work of Terry Lee Lindenmuth in GeoGebra.
Following the teacher demonstration, give students 5 minutes of quiet work time, then 10 minutes of group work followed by a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Work with your group to decide which person will use each spinner. Make sure each person selects a different spinner.
Answer the first set of questions on your own.
Spinner A
Spinner B
Spinner C
Spinner D
- Spin your spinner 10 times and record your outcomes.
- Did you get all of the different possible outcomes in your 10 spins?
-
What fraction of your 10 spins landed on 3?
Work with your group to answer the next set of questions.
- Share your outcomes with your group and record their outcomes.
- Outcomes for spinner A:
- Outcomes for spinner B:
- Outcomes for spinner C:
- Outcomes for spinner D:
- Do any of the spinners have the same sample space? If so, do they have the same probabilities for each number to result?
- For each spinner, what is the probability that it ends on the number 3? Explain or show your reasoning.
- For each spinner, what is the probability that it lands on something other than the number 3? Explain or show your reasoning.
- Noah put spinner D on top of his closed binder and spun it 10 times. It never landed on the number 1. How might you explain why this happened?
- Han put spinner C on the floor and spun it 10 times. It never landed on the number 3, so he says that the probability of getting a 3 is 0. How might you explain why this happened?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 4. Provide 1 set of 4 spinners cut from the blackline master to each group. Each student will need a pencil and paper clip. Demonstrate how to use a pencil and paper clip to spin the spinner: Unbend one end of the paper clip so that it is straight. Put the paper clip on the end of the pencil and the pencil tip at the center of the spinner. Spin the paper clip so that it rotates around the pencil and the unbent portion points to the result of the spin. If it is difficult to determine which section the end of the paper clip points to, it is okay to disregard that spin and spin again.
Classes using the digital curriculum have spinner applets to use if they choose to. These applets are based on the work of Terry Lee Lindenmuth in GeoGebra.
Following the teacher demonstration, give students 5 minutes of quiet work time, then 10 minutes of group work followed by a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Your teacher will give you 4 spinners. Make sure each person in your group uses a different spinner.
- Spin your spinner 10 times, and record your outcomes.
- Did you get all of the different possible outcomes in your 10 spins?
-
What fraction of your 10 spins landed on 3?
-
Next, share your outcomes with your group, and record their outcomes.
- Outcomes for spinner A:
- Outcomes for spinner B:
- Outcomes for spinner C:
- Outcomes for spinner D:
- Do any of the spinners have the same sample space? If so, do they have the same probabilities for each number to result?
- For each spinner, what is the probability that it lands on the number 3? Explain or show your reasoning.
- For each spinner, what is the probability that it lands on something other than the number 3? Explain or show your reasoning.
- Noah put spinner D on top of his closed binder and spun it 10 times. It never landed on the number 1. How might you explain why this happened?
- Han put spinner C on the floor and spun it 10 times. It never landed on the number 3, so he says that the probability of getting a 3 is 0. How might you explain why this happened?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Design a spinner that has a \(\frac{2}{3}\) probability of landing on the number 3. Explain how you could precisely draw this spinner.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think they need to have their probability estimates match the computed probability. Remind them of the activity "Due For a Win" to see why we might expect the estimated probability and the calculated probability to be a little different.
Activity Synthesis
The purpose of this discussion is to think about reasons why the estimate of a probability may be different from the actual probability.
Select some students to share their responses to the last 5 questions.
Ask, "How does your fraction of 3 spins compare to the probability you expect from just looking at the spinner?"
Explain that although the spinners provided were designed to have equally sized sections (except for spinner D which has the angles \(180^\circ, 45^\circ,\) and \(90^\circ\)), sometimes it may be difficult to determine when the sections are exactly the same size. For some situations where things are not so evenly divided, some experimenting may be needed to determine that the outcomes actually follow the probability we might expect.
There are two main reasons why the fraction of the time an event occurs may differ from the actual probability:
- The simulation was designed or run poorly.
- Maybe the spinner sections were not equal sized when they should be or maybe the spinner was tilted.
- Maybe the items being chosen from the bag were different sizes, so you were more likely to grab one than another.
- Maybe the coin or number cube are not evenly weighted and are more likely to land with one side up than others.
- Maybe the computer that was programmed to return a random number has a problem with the code that returns some numbers more often than others.
- Not enough trials were run.
- As in the previous lesson, if you flip a coin once and it comes up heads, that doesn’t mean that it always will. Even if you flip it 100 times, it’s not guaranteed to land heads up exactly 50 times, so some slight deviation is to be expected.
Design Principle(s): Support sense-making; Cultivate conversation
5.3: How Much Green? (10 minutes)
Activity
In the previous activity, students could see the entire spinner and compute the probability to compare with their experimental results. In many contexts, it is not possible to know the entire sample space or compute an exact probability from the situation itself. For example, the probability of rain tomorrow usually cannot be exactly estimated from available information. In this activity, students see how to approach such problems by estimating the probability of an event using the results from repeating trials (MP8). In this particular example, the exact probability can be computed when the information is revealed, so students can compare their results to this value. In situations like predicting the weather, estimates may be the best thing we have available. Students gain exposure to the process of drawing blocks from a bag, which will be useful in designing simulations in future lessons.
Launch
Arrange students in groups of 3–4. Distribute 1 paper bag containing 5 snap cubes (3 green cubes and 2 cubes of some other color that match each other) to each group. 5 minutes of group work followed by a whole-class discussion.
Design Principle(s): Maximize meta-awareness
Student Facing
Your teacher will give you a bag of blocks that are different colors. Do not look into the bag or take out more than 1 block at a time. Repeat these steps until everyone in your group has had 4 turns.
- Take one block out of the bag and record whether or not it is green.
- Put the block back into the bag, and shake the bag to mix up the blocks.
- Pass the bag to the next person in the group.
- What do you think is the probability of taking out a green block from this bag? Explain or show your reasoning.
- How could you get a better estimate without opening the bag?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may estimate a probability that is different from the fraction of times they draw a green block. Ask these students for a reason they chose a different value for their estimate.
Activity Synthesis
The purpose of the discussion is to show that estimating the probability of an event can be done using repeated trials and is usually improved by including more trials.
Ask each group how many green blocks they got in their trials and display the class results for all to see.
Consider asking these discussion questions:
- "How can we use the values from the class to estimate the probability of drawing out a green block?" (By using the data we have, we can estimate the fraction of blocks that are green.)
- "Based on the class data, what is the estimated probability of choosing a green block from the bag?"
- "Was the probability estimated from the class data different from the probability estimate based on the data just from your group? Why?" (Yes, since not everyone picked out the same thing each time.)
- "Some of you may have felt that there are 5 blocks in the bag. If we use that information, does that change our estimate of the probability?" (If there are only 5 blocks, it only makes sense for the probability to be \(0, \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5},\) or \(\frac{5}{5}\).)
- Allow students to open the bags and see what blocks are in there. "What is the probability based on this observation?" (\(\frac{3}{5}\))
- "Does it match your group estimates? Does it match the class estimates?"
- "Was the estimate from the class data more accurate than the estimates from the groups?" (It should be since more trials are included.)
Lesson Synthesis
Lesson Synthesis
Consider asking these discussion questions:
- "A student repeats the process of taking blocks out of a bag and replacing them 100 times. A green block is drawn 67 times. What is a good estimate for the probability of drawing out a green block from the bag?" (\(\frac{67}{100}\))
- "A chance experiment is done a few times and the fraction of outcomes in a certain event is used as an estimate for the probability of the event. If the experiments are done carefully, how could the estimate be improved?" (Usually, the more trials done for an experiment, the closer the estimate will be to a computed probability.)
- "A chance experiment is repeated many times, but the fraction of outcomes for which a certain event occurs does not match the actual probability of the event. What are some reasons this may happen?" (The experiment may not have been repeated enough times. The experiment was badly done. For example, the experiment may not have been as random as originally thought. We usually expect a little difference between the estimated probability and the actual probability.)
5.4: Cool-down - The Probability of Spinning B (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Suppose a bag contains 5 blocks. If we select a block at random from the bag, then the probability of getting any one of the blocks is \(\frac15\).

Now suppose a bag contains 5 blocks. Some of the blocks have a star, and some have a moon. If we select a block from the bag, then we will either get a star block or a moon block. The probability of getting a star block depends on how many there are in the bag.
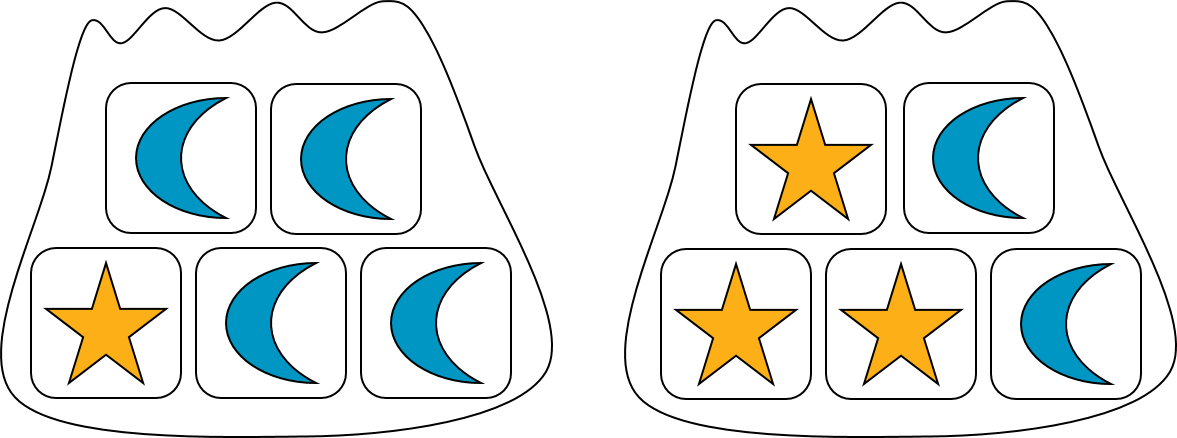
In this example, the probability of selecting a star block at random from the first bag is \(\frac15\), because it contains only 1 star block. (The probability of getting a moon block is \(\frac45\).) The probability of selecting a star block at random from the second bag is \(\frac35\), because it contains 3 star blocks. (The probability of getting a moon block from this bag is \(\frac25\).)
This shows that two experiments can have the same sample space, but different probabilities for each outcome.