Lesson 11
Comparing Groups
11.1: Notice and Wonder: Comparing Heights (5 minutes)
Warm-up
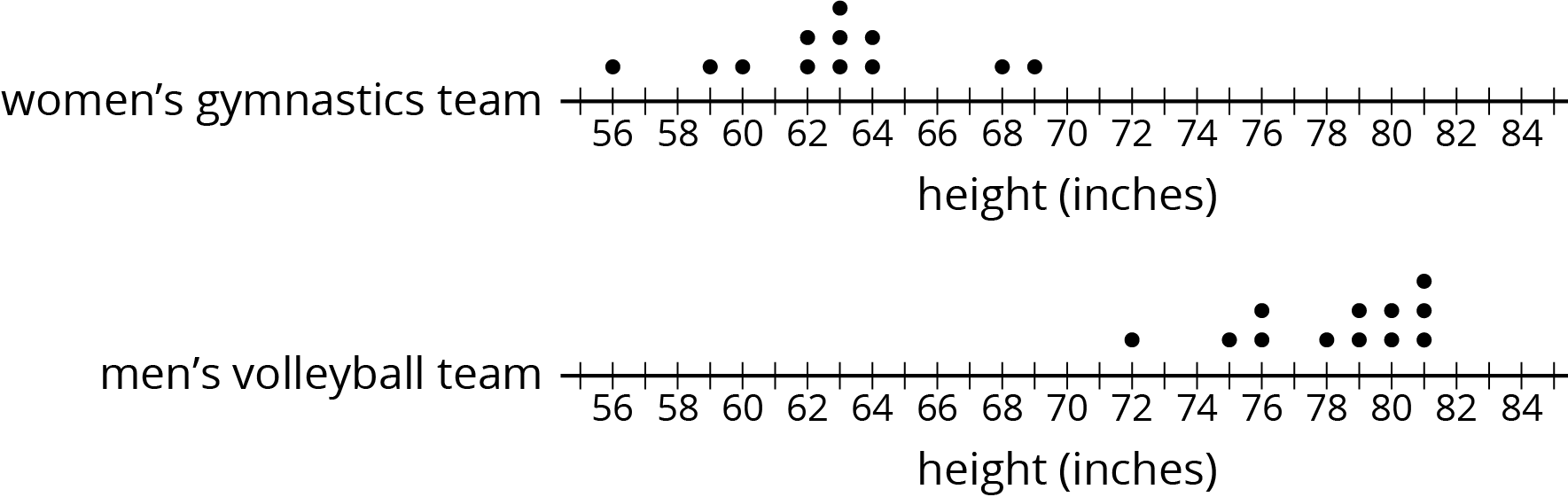
The purpose of this warm-up is to collect ideas that will be useful in the discussions in this lesson. While students may notice and wonder many things about these images, the methods of showing that the volleyball team is much taller than the gymnastic team are the important discussion points.
Launch
Arrange students in groups of 2. Tell students that they will look at the dot plots, and their job is to think of at least one thing they notice and at least one thing they wonder. Display the dot plots for all to see. Ask students to give a signal when they have noticed or wondered about something. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Student Facing
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. If possible, record the relevant reasoning on or near the image. After each response, ask the class if they agree or disagree and to explain alternative ways of thinking, referring back to the images each time. If the definitive difference in height does not come up during the conversation, ask students to discuss this idea.
The next activity looks more closely at comparing these data sets. It is not necessary to have students calculate anything (mean, median, MAD, IQR) yet.
11.2: More Team Heights (15 minutes)
Activity
In this activity, students are asked to compare the heights of two groups of people. The wording of the questions allows for multiple interpretations and any reasonable answer should be accepted (MP1). This activity also provides an opportunity to remind students of how to analyze dot plots as well as how to calculate the measures of center and variability of the data.
Launch
Keep students in groups of 2.
Display the dot plots from the warm-up activity and help students see that the data sets given in their books or devices match the numbers shown in the dot plots.
For the problem addressing the tennis and badminton teams, you may suggest each student create a dot plot of one of the groups and then compare with their partner.
Allow students 10 minutes of partner work time followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
-
How much taller is the volleyball team than the gymnastics team?
-
Gymnastics team’s heights (in inches) : 56, 59, 60, 62, 62, 63, 63, 63, 64, 64, 68, 69
-
Volleyball team’s heights (in inches): 72, 75, 76, 76, 78, 79, 79, 80, 80, 81, 81, 81
-
-
Make dot plots to compare the heights of the tennis and badminton teams.
-
Tennis team’s heights (in inches): 66, 67, 69, 70, 71, 73, 73, 74, 75, 75, 76
-
Badminton team’s heights (in inches): 62, 62, 65, 66, 68, 71, 73
What do you notice about your dot plots?
-
- Elena says the members of the tennis team were taller than the badminton team. Lin disagrees. Do you agree with either of them? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to think about ways we could approach comparing two groups as well as have an opportunity to review dot plots, measures of center, and measures of variation from prior grades.
Ask, “What are some ways we can compare groups of things?” At this stage, students are only expected to informally compare the groups. Although a consistent “general rule” for comparing groups will be introduced in later lessons, this activity is about getting a general idea that some groups (like the gymnastics and volleyball teams) have a rather clear difference while others (like the tennis and badminton teams) may be more alike.
Ask students about the distribution of the data shown in the dot plots. Make sure to highlight the shape, center, and spread. Review how to find the mean as a measure of the center of a data set. Review how to calculate the mean absolute deviation (MAD) as a measure of the variability of a data set. Students may mention median and interquartile range (IQR) as other ways to measure center and variability. Although median and IQR are not needed in this activity, it may be useful to review how to calculate those values as well. Both measures of center and variability will be used later in the unit.
Introduce the idea of judging how much two data sets overlap.
Design Principle(s): Support sense-making
11.3: Family Heights (15 minutes)
Activity
Following the review from the previous activity, students are asked to use these calculations to compare two groups more formally. Students are shown one quantifiable method of determining whether the two groups are relatively close or relatively very different in the discussion following the activity involving describing the difference of the measures of center as a multiple of the variability (MP2). The important idea for students to grasp from this activity is that the measures of center and measures of variability of the groups work together to give an idea of how similar or different the groups are.
As students work to compare heights of the two families, monitor for students who:
- Create dot plots of the data and look at the overlap visually.
- Compute measures of center to compare the groups numerically.
- Also compute measures of variability to compare the measures of center for each group accounting for the spread of values.
Launch
Keep students in groups of 2.
Introduce students to the idea that both the measures of center as well as the measures of variability are important when comparing data sets by asking students about these contexts.
- “Two groups of adults have mean weights that are different by 10 pounds. Are the two groups very different in weight?”
- “Two groups of 8 year olds have weights that are different by 10 pounds. Are the two groups very different in weight?”
- “Two groups of birds have weights that are different by 3.2 ounces (0.2 pounds). Are the two groups very different in weight?”
Without knowing more about the exact numbers, it seems that the adults might not be that different. A typical adult might weigh 180 pounds and, depending on diet and activity, even one person’s weight might go up or down by 10 pounds in a few weeks. It might be hard to tell these two groups apart even with the 10 pound difference in means.
On the other hand, 8 year olds typically weigh about 50 pounds, so a 10 pound difference can mean a lot more. A group with an average weight of 50 pounds is 25% heavier than a group with an average weight of 40 pounds.
For the birds, it might be hard to say how different the groups are unless we have more information. If the two groups contain the same type of bird (e.g., parrots), we might expect the weights to be fairly consistent, so a 3.2 ounce difference could be a lot. If the two groups each contain a variety of types (from hummingbirds up to emus), the 3.2 ounce difference might not be very much.
Based on these examples, it helps to know not only the means (or medians), but also the variability of the groups. We saw this in the previous activity with the overlap in the dot plots.
For the work in this activity, tell students to try to give some values to help back up their comparison of the two groups.
Allow students 1 minute of quiet think time to examine ways of approaching the problem, followed by partner work time and a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Optimize output (for comparison); Maximize meta-awareness
Student Facing
Compare the heights of these two families. Explain or show your reasoning.
-
The heights (in inches) of Noah’s family members: 28, 39, 41, 52, 63, 66, 71
-
The heights (in inches) of Jada’s family members: 49, 60, 68, 70, 71, 73, 77
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
If Jada's family adopts newborn twins who are each 18 inches tall, does this change your thinking? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to begin to be more formal in their comparison of data from different groups. In particular, a general rule is established that will be used in this unit.
Select students to share their approaches in the sequence outlined in the Activity Narrative.
The heights of Noah’s and Jada’s families overlap more than the heights of the gymnastics and volleyball teams. The difference in means for the two families is about the same as between the two teams.
- The difference between the mean heights of the volleyball and gymnastics teams is \(78.17 - 62.75\), or 15.42 inches.
- The difference between the mean heights of Jada’s and Noah’s families is \(66.86 - 51.43\), or 15.43 inches. The variability in heights for the families is greater than the variability in heights for the teams.
Explain: The difference between the means is not enough information to know whether or not the data sets are very different. One way to express the amount of overlap is to divide the difference in means by the (larger) mean absolute deviation.
Demonstrate for students how to do this calculation for the volleyball and gymnastics teams:
-
The difference in means is more than 6 times the measure of variability, because \(15.42 \div 2.46 \approx 6.3\).
Leave the calculation for the two teams displayed. Ask students to do the calculation for Jada’s and Noah’s families.
-
The difference in means is a little more than 1 time the measure of variability, because \(15.43 \div 13.22 \approx 1.2\).
As a general rule, we will consider it a large difference between the data sets if the difference in means is more than twice the mean absolute deviation. If the mean absolute deviation is different for each group, use the larger one for this calculation.
For students who ask why twice the MAD is used rather than some other value, defer the question for later in the unit. A later lesson titled Do They Carry More? will address this question in more detail.
11.4: Track Length (10 minutes)
Optional activity
In this activity, students continue to review the meaning of mean and mean absolute deviation as well as practice using the method they were shown in the previous activity to compare multiple groups based on their means and measure of variability. Students begin by matching information about a set of data to its dot plot and calculating the mean and mean absolute deviation for the remaining dot plots, then they compare the data sets pairwise using the mean and MAD values (MP3). In the discussion, students are introduced to a way to add extra information to dot plots to visualize the general rule given in the previous activity.
Launch
Keep students in groups of 2. Give students 5 minutes of partner work time followed by a whole-class discussion.
Student Facing
Here are three dot plots that represent the lengths, in minutes, of songs on different albums.
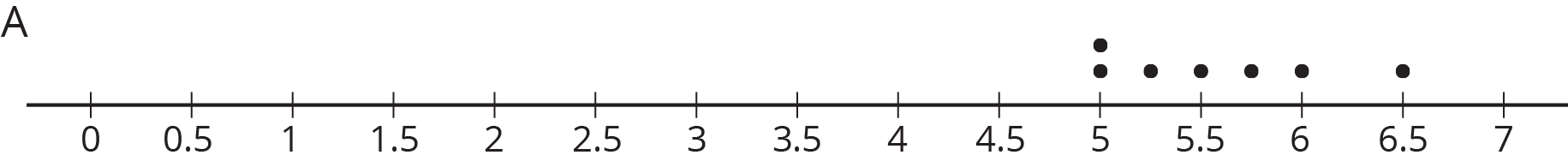


-
One of these data sets has a mean of 5.57 minutes and another has a mean of 3.91 minutes.
- Which dot plot shows each of these data sets?
- Calculate the mean for the data set on the other dot plot.
-
One of these data sets has a mean absolute deviation of 0.30 and another has a MAD of 0.44.
- Which dot plot shows each of these data sets?
- Calculate the MAD for the other data set.
-
Do you think the three groups are very different or not? Be prepared to explain your reasoning.
-
A fourth album has a mean length of 8 minutes with a mean absolute deviation of 1.2. Is this data set very different from each of the others?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is to help students visualize the calculations they performed.
Ask, “Before calculating any of the values, would you have guessed that dot plots B and C would not be very different, but A would be very different from the other two? Explain your reasoning.” (Yes, since there is some overlap between the data of dot plots B and C, but the data in A does not overlap very much with B and not at all with C.)
Demonstrate a technique for students to see the the general rule on the dot plots using dot plot A. Mark the mean of the data set on the dot plot with a triangle, then draw a line segment from the triangle so that its length is 2 MADs in each direction. On dot plot A, draw a triangle at 5.57 and a line segment from 4.69 (\(5.57 - 2 \boldsymbol{\cdot} 0.44\)) to 6.45 (\(5.57 + 2 \boldsymbol{\cdot} 0.44\)) as in the image here.

Lesson Synthesis
Lesson Synthesis
Consider asking these questions for discussion:
- “What does a dot plot tell you?”
- “What are some measures of center, and how are they calculated?”
- “Why is a measure of center useful for comparing two groups?”
- “Why is a measure of variability also needed when comparing two groups?”
- “What is the general rule we will use to determine whether two groups have a large difference or not?”
11.5: Cool-down - Prices of Homes (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Comparing two individuals is fairly straightforward. The question "Which dog is taller?" can be answered by measuring the heights of two dogs and comparing them directly. Comparing two groups can be more challenging. What does it mean for the basketball team to generally be taller than the soccer team?
To compare two groups, we use the distribution of values for the two groups. Most importantly, a measure of center (usually mean or median) and its associated measure of variability (usually mean absolute deviation or interquartile range) can help determine the differences between groups.
For example, if the average height of pugs in a dog show is 11 inches, and the average height of the beagles in the dog show is 15 inches, it seems that the beagles are generally taller. On the other hand, if the MAD is 3 inches, it would not be unreasonable to find a beagle that is 11 inches tall or a pug that is 14 inches tall. Therefore the heights of the two dog breeds may not be very different from one another.