Lesson 2
Chance Experiments
2.1: Which is More Likely? (5 minutes)
Warm-up
The purpose of this warm-up is to engage students' intuition about likelihood of events. The following activities in this lesson continue to develop more formal ways of thinking about likelihood leading to the definition of probability in the next lesson.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet work time and time to share their response with a partner. Follow with a whole-class discussion.
Student Facing
Which is more likely to happen?
-
When reaching into a dark closet and pulling out one shoe from a pile of 20 pairs of shoes, you pull out a left shoe.
-
When listening to a playlist—which has 5 songs on it—in shuffle mode, the first song on the playlist plays first.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think that it is required to pull out a specific shoe rather than any left shoe. Ask students to visualize the problem and determine how many left shoes are in the closet.
Activity Synthesis
The purpose of the discussion is to help students recognize their own intuition about the likelihood of an event even when prior outcomes are not available.
Have partners share responses with the class, and ask at least one student for each option for their reasoning. Give students time to discuss their reasoning until they come to an agreement.
It may be helpful to reiterate that the outcomes from these actions are not certain. It is certainly possible to do both things and draw out a right shoe and listen to the first song on the list first, but it is not very likely based on the situations.
2.2: How Likely Is It? (10 minutes)
Activity
As preparation for talking about probability, students are asked to engage their intuition about the concept by loosely grouping scenarios into categories based on their likelihood by reasoning abstractly about situations in context as in MP2. Some of the categories are meant to be loosely interpreted while others (such as "certain" and "impossible") have more precise meanings.
Launch
Arrange students in groups of 2.
Tell students that a “standard number cube” is an object that has the numbers 1 through 6 printed on a cube so that each face shows a different number. This item will be referenced throughout the unit.
It may help students to understand the categories of likelihood with an example of opening a book to a random page:
- Impossible: Opening a 100 page book to page -300.
- Unlikely: Opening a 100 page book to exactly page 45.
- Equally likely as not: Opening a 100 page book to a page numbered less than 51.
- Likely: Opening a 100 page book to a page numbered greater than 10.
- Certain: Opening a 100 page book to a page numbered less than 1,000.
Allow students 5--7 minutes quiet work time followed by partner and whole-class discussion.
Supports accessibility for: Organization; Attention; Social-emotional skills
Design Principle(s): Support sense-making; Optimize output (for explanation)
Student Facing
-
Label each event with one of these options:
impossible, unlikely, equally likely as not, likely, certain
- You will win grand prize in a raffle if you purchased 2 out of the 100 tickets.
- You will wait less than 10 minutes before ordering at a fast food restaurant.
- You will get an even number when you roll a standard number cube.
- A four-year-old child is over 6 feet tall.
- No one in your class will be late to class next week.
- The next baby born at a hospital will be a boy.
g. It will snow at our school on July 1.
h. The Sun will set today before 11:00 p.m.
i. Spinning this spinner will result in green.
j. Spinning this spinner will result in red.
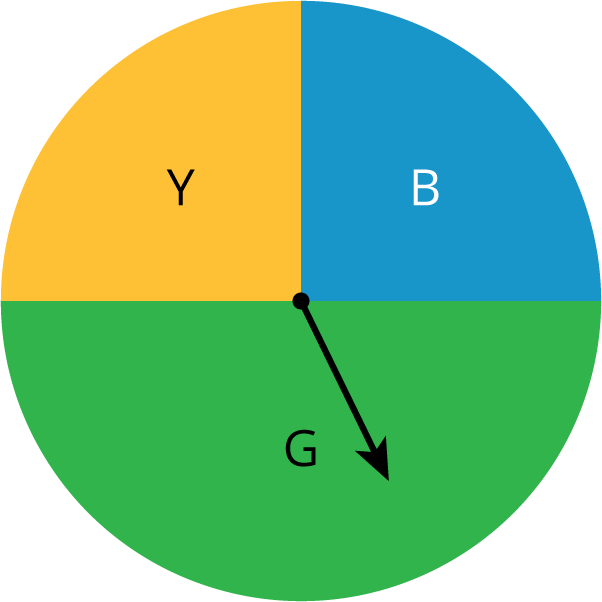
- Discuss your answers to the previous question with your partner. If you disagree, work to reach an agreement.
-
Invent another situation for each label, for a total of 5 more events.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to see that the loose categories can be understood in a more formal way. Some students may begin to attach numbers to the likelihood of the events and that is a good way to begin the transition to thinking about probability.
There may be some discussion about the category "equally likely as not." Are events in this category required to be at exactly 50% or would an event with 55% or 48% likelihood be placed in this category as well? At this stage, the categories are meant to be loose, so it is not necessary that everyone agree on what goes in each category.
Questions for discussion
- "Were any of the scenarios listed difficult to categorize?"
- "Which categories are the most strict about what can go in them?" ("Certain" should represent scenarios that must happen with 100% certainty. "Impossible" should represent scenarios that cannot happen.)
- "What does it mean for an event to be certain?" (That it must happen.)
- "What does it mean for an event to be likely?" (Between about 50% and 100% chance.)
2.3: Take a Chance (10 minutes)
Activity
In this lesson, students begin to move towards a more quantitative understanding of likelihood by observing a game that has two rounds with different requirements for winning in each round. The game is also played multiple times to help students understand that the actual number of times an outcome occurs may differ from expectations based on likelihood at first, but should narrow towards the expectation in the long-run. By repeating the process many times, students engage in MP8 by recognizing a structure beginning to form with the results. Activities in later lessons will more formally show this structure forming from the repeated processes.
Launch
Arrange students in groups of 2. Following the demonstration game, allow 5 minutes of partner work followed by a whole-class discussion.
Have the students play this game of chance 10 times by playing the two rounds each time. Display the results of each round for all to see. For example:
| person choosing number | winner | chooser wins? |
|---|---|---|
| Lin | Noah | |
| Lin | Lin | X |
| Noah | Noah | X |
| Lin | Lin | X |
Tell students that the questions ask about whether the person choosing the number wins the game or not. They should not concentrate on who won more often, but how often the number chooser wins the round. In the example table, the column with the Xs is the focus.
The digital version is slightly different, with an applet generating random numbers from 1 to 6. This applet is based on the work of pirsquared in GeoGebra.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
This applet displays a random number from 1 to 6, like a number cube. With a partner, you will play a game of chance.
-
In the first round, one of you will score on an even roll and one of you will score on an odd roll. You decide that first.
-
In the second round, the winner of round 1 will score on numbers \(1 - 4\), and the other player will score on numbers \(5 - 6\).
-
Each round is 10 rolls. Be sure to turn on "History" after your first roll and wait for it to update before rolling again.
- When each player had three numbers, did one of them usually win?
- When one player had four numbers, did you expect them to win? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Following the demonstration game, allow 5 minutes of partner work followed by a whole-class discussion.
Select two students to play this game of chance that consists of 2 rounds. Give 1 standard number cube to each student.
Round 1: One student chooses three numbers that will count as a win for them. The other student wins if any of the other numbers come up. Roll the number cube.
Round 2: Whoever lost the first round gets to choose 4 numbers that will count for a win for them while their partner gets the remaining 2 numbers. Roll the number cube.
Have the students play this game of chance 10 times by playing the two rounds each time. Display the results of each round for all to see. For example:
| person choosing number | winner | chooser wins? | |
|---|---|---|---|
| game 1, round 1 | Lin | Noah | |
| game 1, round 2 | Lin | Lin | X |
| game 2, round 1 | Noah | Noah | X |
| game 2, round 2 | Lin | Lin | X |
Tell students that the questions ask about whether the person choosing the number wins the game or not. They should not concentrate on who won more often, but how often the number chooser wins the round. In the example table, the column with the Xs is the focus.
The digital version is slightly different, with an applet generating random numbers from 1 to 6. This applet is based on the work of pirsquared in GeoGebra.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Your teacher will have 2 students play a short game.
- When the first person chose 3 numbers, did they usually win?
- When the person chose 4 numbers, did you expect them to win? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
On a game show, there are 3 closed doors. One door has a prize behind it. The contestant chooses one of the doors. The host of the game show, who knows where the prize is located, opens one of the other doors which does not have the prize. The contestant can choose to stay with their first choice or switch to the remaining closed door.
- Do you think it matters if the contestant switches doors or stays?
-
Practice playing the game with your partner and record your results. Whoever is the host starts each round by secretly deciding which door has the prize.
- Play 20 rounds where the contestant always stays with their first choice.
- Play 20 more rounds where the contestant always switches doors.
- Did the results from playing the game change your answer to the first question? Explain.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Define a chance experiment. A chance experiment is the process of making an observation of something when there is uncertainty about which of two or more possible outcomes will occur. Each time a standard number cube is thrown, it is a chance experiment. This is because we cannot be certain of which number will be the outcome of this experiment.
Some questions for discussion:
- "Who did you expect to win each time: the person choosing the number or the other person? Explain your reasoning."
- "In one round of the game it was more likely that the person choosing the numbers would win. We’ll be talking a lot in this unit about how likely or probable an event is to happen and even assigning numbers to the likelihood."
- "What if we had to assign numbers to the 'likelihood' of the person choosing the numbers winning for each round? For each part of the game, what percentage or fraction would you assign to the likelihood of the person who chose the numbers winning?" (For the first round of the game, there is a 50% or \(\frac{1}{2}\) chance for each person to win. For the second round of the game, the person choosing the numbers should have a 67% or \(\frac{4}{6}\) or \(\frac{2}{3}\) chance to win.)
- "What percentage or fraction would you assign to waiting for less than 10 minutes before your order is taken at the fast food restaurant from the previous task?" (Answers vary. Values between 80% and 100% are expected. It is not necessary to agree on a particular value at this point.)
- "How could we get more evidence to support these answers?" (Collect data from fast food restaurants to find a fraction of customers who order their food within 10 minutes.)
2.4: Card Sort: Likelihood (10 minutes)
Activity
The last activity in this lesson moves one more step closer to quantifying likelihood of scenarios by ordering them individually rather than into groups. Some of the scenarios have a numerical probability expressed as a percentage, some in decimal form, some as a fraction, and some do not have a numerical probability given (MP7). This gives students the opportunity to work with probabilities expressed as percentages, decimals, and fractions.
You will need the blackline master for this activity.
Launch
Arrange students in groups of 3. Distribute one copy of the blackline master for each group.
Tell students to take turns ordering the cards by beginning with one card, then adding in additional cards one at a time before, after, or between cards as needed.
Give students 5 minutes for group work followed by a whole-class discussion.
Student Facing
-
Your teacher will give you some cards that describe events. Order the events from least likely to most likely.
-
After ordering the first set of cards, pause here so your teacher can review your work. Then, your teacher will give you a second set of cards.
-
Add the new set of cards to the first set so that all of the cards are ordered from least likely to most likely.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may have trouble understanding the Rock, Paper, Scissors context. Tell these students that a player randomly chooses one of the three items to play in each round. If students still struggle, tell them that each of the three items are expected to be played with equal likelihood.
Activity Synthesis
The purpose of the discussion is for students to talk about the methods they used to sort the cards and compare likelihood of different situations.
Some questions for discussion:
- "How were the numerical values of the likelihoods written?" (Some were written as percentages, some as fractions, and some as decimal values.)
- "How did you compare them when there was a mix of percentages, fractions, and decimals?"
- "Some of the cards did not have a percentage, fraction, or decimal. How did you determine where those cards would go in the order?"
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Ask students “what is a chance event?”
In the same groups of 2, have partners come up with examples of each of these types of events:
- impossible
- unlikely
- equally likely as not
- likely
- certain
Ask partners to share responses with the class.
2.5: Cool-down - According To (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A chance experiment is something that happens where the outcome is unknown. For example, if we flip a coin, we don’t know if the result will be a head or a tail. An outcome of a chance experiment is something that can happen when you do a chance experiment. For example, when you flip a coin, one possible outcome is that you will get a head. An event is a set of one or more outcomes.
We can describe events using these phrases:
- Impossible
- Unlikely
- Equally likely as not
- Likely
- Certain
For example, if you flip a coin:
- It is impossible that the coin will turn into a bottle of ketchup.
- It is unlikely the coin will land on its edge.
- It is equally likely as not that you will get a tail.
- It is likely that you will get a head or a tail.
- It is certain that the coin will land somewhere.
The probability of an event is a measure of the likelihood that an event will occur. We will learn more about probabilities in the lessons to come.