Lesson 3
What Are Probabilities?
3.1: Which Game Would You Choose? (5 minutes)
Warm-up
The purpose of this warm-up is for students to choose the more likely event based on their intuition about the possible outcomes of two chance experiments. The activities in this lesson that follow define probability and give ways to compute numerical values for the probability of chance events such as these.
Launch
Arrange students in groups of 2. Give students 1 minute of quiet work time followed by time to share their response with a partner. Follow with a whole-class discussion.
Student Facing
Which game would you choose to play? Explain your reasoning.
Game 1: You flip a coin and win if it lands showing heads.
Game 2: You roll a standard number cube and win if it lands showing a number that is divisible by 3.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have trouble comparing \(\frac{1}{2}\) and \(\frac{2}{6}\). Review how to compare fractions with these students.
Some students may struggle with the wording of the second game. Help them understand what it means for a number to be divisible by a certain number and consider providing them with a standard number cube to examine the possible values.
Activity Synthesis
Have partners share their answers and display the results for all to see. Select at least one student for each answer provided to give a reason for their choice.
If no student mentions it, explain that the number of possible outcomes that count as a win and the number of total possible outcomes are both important to determining the likelihood of an event. That is, although there are two ways to win with the standard number cube and only one way to win on the coin, the greater number of possible outcomes in the second game makes it less likely to provide a win.
3.2: What’s Possible? (15 minutes)
Activity
Following the warm-up discussion in which the importance of the number of possible outcomes from an experiment is discussed, students are introduced to the term sample space. Students examine experiments to determine the set of outcomes in the sample space and then use the sample spaces to think about the likelihood of the events. Following the activity, students engage in MP6 by attaching numerical values to the likelihood of events through the word probability.
In some cases, the actual sample space is unknown. For example, in the warm-up for the first lesson of this unit, all the different types of fish in the lake may not be known. In these cases, probabilities may be less precise, but can still be estimated based on the outcomes from previous experiments. Students will begin to explore this idea in the next activity and later lessons will explore the concept in more detail.
Launch
Arrange students in groups of 2.
Define random as doing something so that the outcomes are based on chance. An example is putting the integers 1 through 20 on a spinner with each number in an equal sized section. Something that is not random might be answering a multiple choice question on a test for a subject you've studied.
Explain that, for a chance experiment, each possible result is called an outcome. The set of all possible outcomes is called the sample space. Spinning a spinner with equal sized sections marked 1 through 20 has a possible outcome of 8, but neither heads nor green is a possible outcome. The sample space is made up of all integers from 1 through 20.
Give students 10 minutes of partner work time followed by whole-class discussion.
Student Facing
-
For each situation, list the sample space and tell how many outcomes there are.
- Han rolls a standard number cube once.
-
Clare spins this spinner once.
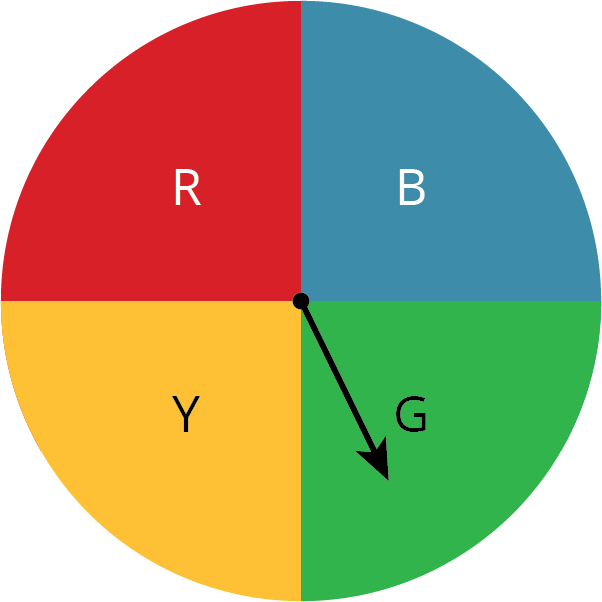
- Kiran selects a letter at random from the word “MATH.”
- Mai selects a letter at random from the alphabet.
- Noah picks a card at random from a stack that has cards numbered 5 through 20.
-
Next, compare the likelihood of these outcomes. Be prepared to explain your reasoning.
- Is Clare more likely to have the spinner stop on the red or blue section?
- Is Kiran or Mai more likely to get the letter T?
- Is Han or Noah more likely to get a number that is greater than 5?
- Suppose you have a spinner that is evenly divided showing all the days of the week. You also have a bag of papers that list the months of the year. Are you more likely to spin the current day of the week or pull out the paper with the current month?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Are there any outcomes for two people in this activity that have the same likelihood? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Note that all of the outcomes are equally likely within each sample space. This is not always the case, but it is in these examples.
Explain that sometimes it is important to have an actual numerical value rather than a vague sense of likelihood. To answer how probable something is to happen, we assign a probability.
Probabilities are values between 0 and 1 and can be expressed as a fraction, decimal, or percentage. Something that has a 50% chance of happening, like a coin landing heads up, can also be described by saying, “The probability of a coin landing heads up is \(\frac{1}{2}\).” or “The probability of the coin landing heads up is 0.5.”
When each outcome in the sample space is equally likely, we may calculate the probability of a desired event by dividing the number of outcomes for which the event occurs by the total number of outcomes in the sample space.
- "A standard number cube is rolled. What is the sample space?" (1, 2, 3, 4, 5, 6)
- "How many outcomes are in the sample space?" (6)
- "What is the probability of rolling a 3? Explain your reasoning." (\(\frac{1}{6}\) since there is a single 3 and 6 outcomes in the sample space.)
- "An experiment has one of each different possible outcome. The probability of getting one of the outcomes is \(\frac{1}{30}\). How many outcomes are in the sample space?" (30)
Supports accessibility for: Conceptual processing; Language; Memory
Design Principle(s): Optimize output (for explanation)
3.3: What’s in the Bag? (15 minutes)
Activity
In this activity, students are introduced to the idea that not all sample spaces are obvious before actually doing the experiment. Therefore, it is not always possible to calculate the exact probabilities for events before doing or simulating the experiment. In such situations, it is important to reason abstractly about the scenario (MP2) to gain an understanding of the situation. Students refine their guesses about the sample space by repeatedly drawing items from a bag and looking for patterns in this repetition (MP8). In later lessons, students learn how to estimate probabilities from simulations.
You will need the blackline master for this activity.
Launch
Arrange students in groups of 4. Provide each group with a paper bag containing 1 set of slips cut from the blackline master. 10 minutes partner work followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
Your teacher will give your group a bag of paper slips with something printed on them. Repeat these steps until everyone in your group has had a turn.
- As a group, guess what is printed on the papers in the bag and record your guess in the table.
- Without looking in the bag, one person takes out one of the papers and shows it to the group.
- Everyone in the group records what is printed on the paper.
- The person who took out the paper puts it back into the bag, shakes the bag to mix up the papers, and passes the bag to the next person in the group.
| Guess the sample space. |
What is printed on the paper? |
|
|---|---|---|
| person 1 | ||
| person 2 | ||
| person 3 | ||
| person 4 |
- How was guessing the sample space the fourth time different from the first?
- What could you do to get a better guess of the sample space?
- Look at all the papers in the bag. Were any of your guesses correct?
- Are all of the possible outcomes equally likely? Explain.
- Use the sample space to determine the probability that a fifth person would get the same outcome as person 1.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think that the phrase "equally likely" means there is a 50% chance of it happening. Tell students that, in this context, each outcome is equally likely if the probability does not change if you change the question to a different outcome in the sample space. For example, "What is the probability you get a letter A from this bag?" has the same answer as the question, "What is the probability you get a letter B from this bag?"
Activity Synthesis
The purpose of this discussion is for students to understand that often, in the real-world, we do not know the entire sample space before doing the experiment. They will learn in later lessons how to estimate the probabilities for such experiments.
Consider asking some of the following questions:
- "After the first paper is drawn, a group guesses, 'A bunch of letter Cs.' What might they have picked on their first paper that would lead to that guess? What could that group get on their second paper that would make them change their guess? Could they get something for the second paper that would make them sure their guess was right?" (They probably picked a letter C on their first draw. Any other letter on the second draw should make them change their guess. No, they might get another C that would make them think they are right, but with only two tries, there is still a good chance that other letters are in the bag.)
- "After the second paper is drawn, a group guesses, 'All of the consonants.' What might they have picked in their first two papers that would lead to that guess? What could that group get on their third paper that would make them change their guess? Could they get something that would make them more sure of their guess?" (They probably picked two consonants on their first two draws. If they picked a vowel, they would have to change their guess. If they picked another consonant, they might feel better about the guess, but should still not be certain of it.)
- "How did you refine your predictions with each round?"
- "If you had a new bag of papers and you took out papers 50 times and never got a 'Z,' would that mean there is no 'Z' in the bag?" (Not necessarily, but it might make me wonder if it's not in there.)
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
Consider asking some of the questions:
- "If you choose one letter at random from the English alphabet, how many outcomes are in the sample space? How many outcomes are in the event that a vowel (not including Y) is chosen?" (There are 26 outcomes in the sample space. There are 5 outcomes that are vowels: A, E, I, O, and U.)
- "What is the sample space of a chance experiment? How is the number of outcomes in the sample space related to the probability of an event if the outcomes in the sample space are equally likely?" (The sample space is the list of possible outcomes for an experiment. When there are more outcomes in the sample space, the probability of a single outcome occurring is lower.)
- "When there are 100 different outcomes in the sample space that are equally likely, what is the probability that a specific outcome will happen?" (\(\frac{1}{100}\) or 1% or 0.01)
3.4: Cool-down - Letter of the Day (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The probability of an event is a measure of the likelihood that the event will occur. Probabilities are expressed using numbers from 0 to 1.
- If the probability is 0, that means the event is impossible. For example, when you flip a coin, the probability that it will turn into a bottle of ketchup is 0. The closer the probability of some event is to 0, the less likely it is.
- If the probability is 1, that means the event is certain. For example, when you flip a coin, the probability that it will land somewhere is 1. The closer the probability of some event is to 1, the more likely it is.
If we list all of the possible outcomes for a chance experiment, we get the sample space for that experiment. For example, the sample space for rolling a standard number cube includes six outcomes: 1, 2, 3, 4, 5, and 6. The probability that the number cube will land showing the number 4 is \(\frac16\). In general, if all outcomes in an experiment are equally likely and there are \(n\) possible outcomes, then the probability of a single outcome is \(\frac{1}{n}\).
Sometimes we have a set of possible outcomes and we want one of them to be selected at random. That means that we want to select an outcome in a way that each of the outcomes is equally likely. For example, if two people both want to read the same book, we could flip a coin to see who gets to read the book first.