Lesson 6
Absolute Value of Numbers
Lesson Narrative
In the past several lessons, students have reasoned about the structure of rational numbers by plotting them on a number line and noting their relative positions and distances from zero. They learned that opposite numbers have the same distance from zero. Students now formalize the concept of a number’s magnitude with the term absolute value. They learn that the absolute value of a number is its distance from zero, which means that opposite numbers have the same absolute value. Students reason abstractly about the familiar contexts of temperature and elevation using the concept and notation of absolute value (MP2).
Learning Goals
Teacher Facing
- Compare rational numbers and their absolute values, and explain (orally and in writing) the reasoning.
- Comprehend the phrase “absolute value” and the symbol $||$ to refer to a number’s distance from zero on the number line.
- Interpret rational numbers and their absolute values in the context of elevation or temperature.
Student Facing
Let’s explore distances from zero more closely.
Learning Targets
Student Facing
- I can explain what the absolute value of a number is.
- I can find the absolute values of rational numbers.
- I can recognize and use the notation for absolute value.
CCSS Standards
Glossary Entries
-
absolute value
The absolute value of a number is its distance from 0 on the number line.
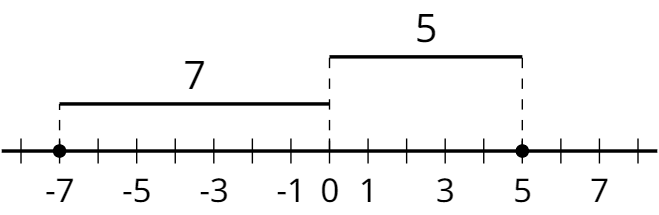
The absolute value of -7 is 7, because it is 7 units away from 0. The absolute value of 5 is 5, because it is 5 units away from 0.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |