Lesson 1
Positive and Negative Numbers
1.1: Notice and Wonder: Memphis and Bangor (5 minutes)
Warm-up
The purpose of this task is to introduce students to temperatures measured in degrees Celsius. Many students have an intuitive understanding of temperature ranges in degrees Fahrenheit that are typical of the city or town in which they live, but many are unfamiliar with the Celsius scale.
Launch
Arrange students in groups of 2. Tell students that they will look at an image, and their job is to think of at least one thing they notice and at least one thing they wonder. Display the image for all to see. Ask students to give a signal when they have noticed or wondered about something. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Student Facing

What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. If possible, record the relevant reasoning on or near the image. After each response, ask the class if they agree or disagree and to explain alternative ways of thinking, referring back to the images each time. Explain to students that temperatures are usually measured in either degrees Fahrenheit, which is what they are probably most familiar with, and degrees Celsius, which may be new for them. Tell them that many other countries measure temperature in degrees Celsius and that scientists use this temperature scale. One thing that is special about the Celsius scale is that water freezes at 0 degrees and boils at 100 degrees (at sea level).
1.2: Above and Below Zero (10 minutes)
Activity
The purpose of this task is to understand that there are natural mathematical questions about certain contexts for which there are no answers if we restrict ourselves to positive numbers. The idea is to motivate the need for negative numbers and to see that there is a natural representation of them on the number line. This task is not about operations with signed numbers, but rather why we extend our number system beyond positive numbers. Students reason abstractly and quantitatively when they represent the change in temperature on a number line (MP2).
Launch
Display this image for all to see.

Tell students, “The thermometer showed a temperature of 7 degrees Celsius one morning. Later, the temperature increased 4 degrees. We can represent this change in temperature using a number line, as shown in the picture.”
Arrange students in groups of 2. Give students 2 minutes of quiet work time for question 1. Give students 2 minutes to compare their responses to their partners and to work on question 2.
Students using the digital version of the curriculum can explore the changes in temperature with the dynamic applet.
Design Principle(s): Support sense-making
Student Facing
1. Here are three situations involving changes in temperature. Represent each change on the applet, and draw it on a number line. Then, answer the question.
-
At noon, the temperature was 5 degrees Celsius. By late afternoon, it has risen 6 degrees Celsius. What was the temperature late in the afternoon?
-
The temperature was 8 degrees Celsius at midnight. By dawn, it has dropped 12 degrees Celsius. What was the temperature at dawn?
-
Water freezes at 0 degrees Celsius, but the freezing temperature can be lowered by adding salt to the water. A student discovered that adding half a cup of salt to a gallon of water lowers its freezing temperature by 7 degrees Celsius. What is the freezing temperature of the gallon of salt water?
2. Discuss with a partner:
-
How did you name the resulting temperature in each situation? Did both of you refer to each resulting temperature by the same name or different names?
-
What does it mean when the resulting temperature is above 0 on the number line? What does it mean when a temperature is below 0?
-
Do numbers below 0 make sense outside of the context of temperature? If you think so, give some examples to show how they make sense. If you don’t think so, give some examples to show otherwise.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Display this image for all to see.

Tell students, “The thermometer showed a temperature of 7 degrees Celsius one morning. Later, the temperature increased 4 degrees. We can represent this change in temperature using a number line, as shown in the picture.”
Arrange students in groups of 2. Give students 2 minutes of quiet work time for question 1. Give students 2 minutes to compare their responses to their partners and to work on question 2.
Students using the digital version of the curriculum can explore the changes in temperature with the dynamic applet.
Design Principle(s): Support sense-making
Student Facing
-
Here are three situations involving changes in temperature and three number lines. Represent each change on a number line. Then, answer the question.
- At noon, the temperature was 5 degrees Celsius. By late afternoon, it has risen 6 degrees Celsius. What was the temperature late in the afternoon?
-
The temperature was 8 degrees Celsius at midnight. By dawn, it has dropped 12 degrees Celsius. What was the temperature at dawn?
- Water freezes at 0 degrees Celsius, but the freezing temperature can be lowered by adding salt to the water. A student discovered that adding half a cup of salt to a gallon of water lowers its freezing temperature by 7 degrees Celsius. What is the freezing temperature of the gallon of salt water?

-
Discuss with a partner:
-
How did each of you name the resulting temperature in each situation?
-
What does it mean when the temperature is above 0? Below 0?
-
Do numbers less than 0 make sense in other contexts? Give some specific examples to show how they do or do not make sense.
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty representing change on the number line. Students sometimes count tick marks rather than counting the space between tick marks when working on a number line. For example, in the original problem image, the arrow on the number line represents a change of 4 degrees. Some students may begin at tick mark 7 and count the tick marks to yield a temperature change of 5 degrees. When reviewing that task with the whole class, be sure to make this important point and demonstrate counting on a number line by highlighting the space between the tick marks while counting out loud.
Activity Synthesis
Some students will use the phrase “degrees below zero.” Use this activity to introduce the term negative as a way to represent a quantity less than zero. In contrast, ask students how they would describe a quantity that is greater than zero on the number line. Some students will have a pre-existing understanding of positive and negative numbers. Discuss the use of + and - as symbols to denote positive and negative numbers. Notation will be important throughout the rest of this unit. Students should understand that +7 and 7 both represent positive 7. Negative 7 is represented as -7.
Supports accessibility for: Conceptual processing; Language; Memory
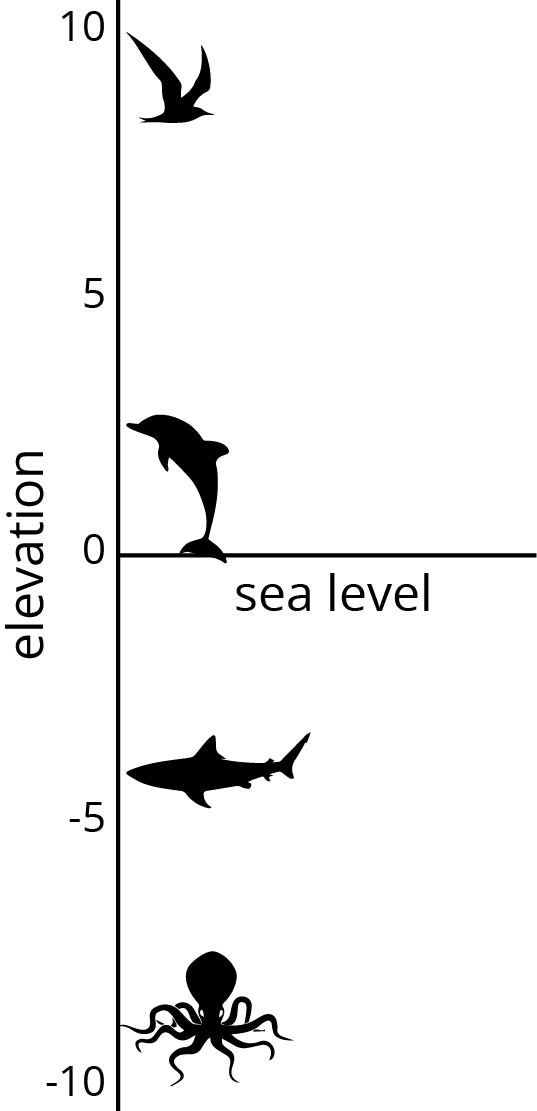
1.3: High Places, Low Places (20 minutes)
Activity
The purpose of this task is to present a second, natural context for negative numbers and to start comparing positive and negative numbers in preparation for ordering them. Monitor for students who make connections between elevation and temperature or come up with strategies for deciding which points are lower or higher than other points. Students may use the structure of a vertical number line in order to compare the relative location of each elevation (MP7).
Launch
Display the table of elevations for all to see. Ask students to think of a way to explain in their own words what the numbers mean. Ask two or three students to share their ideas.
Tell students, “The term ‘elevation’ is commonly used to describe the height of a place (such as a city) or an object (such as an aircraft) compared to sea level. Denver, CO, is called ‘The Mile High City’ because its elevation is 1 mile or 5,280 feet above sea level.”
Arrange students in groups of 2 and give students 5 minutes of quiet work time to answer the first five questions. Ask students to be prepared to explain their thinking in a whole-class discussion.
Students using the digital activity are provided with an interactive map in addition to the questions about elevation. After they complete the questions in the task, they can drag each point to the elevation on the number line for the landmark it represents.
Supports accessibility for: Organization; Attention
Design Principle(s): Support sense-making
Student Facing
-
Here is a table that shows elevations of various cities.
city elevation (feet) Harrisburg, PA 320 Bethell, IN 1,211 Denver, CO 5,280 Coachella, CA -22 Death Valley, CA -282 New York City, NY 33 Miami, FL 0 - On the list of cities, which city has the second highest elevation?
- How would you describe the elevation of Coachella, CA, in relation to sea level?
- How would you describe the elevation of Death Valley, CA, in relation to sea level?
- If you are standing on a beach right next to the ocean, what is your elevation?
- How would you describe the elevation of Miami, FL?
-
A city has a higher elevation than Coachella, CA. Select all numbers that could represent the city’s elevation. Be prepared to explain your reasoning.
- -11 feet
- -35 feet
- 4 feet
- -8 feet
- 0 feet
-
Here are two tables that show the elevations of highest points on land and lowest points in the ocean. Distances are measured from sea level. Drag the points marking the mountains and trenches to the vertical number line and answer the questions.
point mountain continent elevation (meters) C Everest Asia 8,848 H Kilimanjaro Africa 5,895 E Denali North America 6,168 A Pikchu Pikchu South America 5,664 point trench ocean elevation (meters) F Mariana Trench Pacific -11,033 B Puerto Rico Trench Atlantic -8,600 D Tonga Trench Pacific -10,882 G Sunda Trench Indian -7,725 - Which point in the ocean is the lowest in the world? What is its elevation?
- Which mountain is the highest in the world? What is its elevation?
- If you plot the elevations of the mountains and trenches on a vertical number line, what would 0 represent? What would points above 0 represent? What about points below 0?
- Which is farther from sea level: the deepest point in the ocean, or the top of the highest mountain in the world? Explain.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Display the table of elevations for all to see. Ask students to think of a way to explain in their own words what the numbers mean. Ask two or three students to share their ideas.
Tell students, “The term ‘elevation’ is commonly used to describe the height of a place (such as a city) or an object (such as an aircraft) compared to sea level. Denver, CO, is called ‘The Mile High City’ because its elevation is 1 mile or 5,280 feet above sea level.”
Arrange students in groups of 2 and give students 5 minutes of quiet work time to answer the first five questions. Ask students to be prepared to explain their thinking in a whole-class discussion.
Students using the digital activity are provided with an interactive map in addition to the questions about elevation. After they complete the questions in the task, they can drag each point to the elevation on the number line for the landmark it represents.
Supports accessibility for: Organization; Attention
Design Principle(s): Support sense-making
Student Facing
-
Here is a table that shows elevations of various cities.
city elevation (feet) Harrisburg, PA 320 Bethell, IN 1,211 Denver, CO 5,280 Coachella, CA -22 Death Valley, CA -282 New York City, NY 33 Miami, FL 0 - On the list of cities, which city has the second highest elevation?
- How would you describe the elevation of Coachella, CA in relation to sea level?
- How would you describe the elevation of Death Valley, CA in relation to sea level?
- If you are standing on a beach right next to the ocean, what is your elevation?
- How would you describe the elevation of Miami, FL?
-
A city has a higher elevation than Coachella, CA. Select all numbers that could represent the city’s elevation. Be prepared to explain your reasoning.
- -11 feet
- -35 feet
- 4 feet
- -8 feet
- 0 feet
-
Here are two tables that show the elevations of highest points on land and lowest points in the ocean. Distances are measured from sea level.
mountain continent elevation (meters) Everest Asia 8,848 Kilimanjaro Africa 5,895 Denali North America 6,168 Pikchu Pikchu South America 5,664 trench ocean elevation (meters) Mariana Trench Pacific -11,033 Puerto Rico Trench Atlantic -8,600 Tonga Trench Pacific -10,882 Sunda Trench Indian -7,725 - Which point in the ocean is the lowest in the world? What is its elevation?
- Which mountain is the highest in the world? What is its elevation?
- If you plot the elevations of the mountains and trenches on a vertical number line, what would 0 represent? What would points above 0 represent? What about points below 0?
- Which is farther from sea level: the deepest point in the ocean, or the top of the highest mountain in the world? Explain.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A spider spins a web in the following way:
- It starts at sea level.
- It moves up one inch in the first minute.
- It moves down two inches in the second minute.
- It moves up three inches in the third minute.
- It moves down four inches in the fourth minute.
Assuming that the pattern continues, what will the spider’s elevation be after an hour has passed?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty comparing negative elevations. For example, when students are asked to find a higher elevation than Coachella, CA, they may think that -35 feet is a higher elevation than -22 feet because 35 > 22. Encourage students to create a vertical number line and plot elevations before comparing them. Alternatively, provide them with a pre-made number line to use.
Activity Synthesis
The important concept is that elevation measures how far below or above sea level something is. Positive elevation tells us that something is above sea level, whereas negative elevation tells us that something is below sea level. In the same way, positive numbers are greater than zero and negative numbers are less than zero. Zero is neither greater than or less than zero; therefore, it is neither positive or negative. Invite selected students to share their thinking about how they compared different elevations and any similarities they may have noticed between elevation and temperature.
Lesson Synthesis
Lesson Synthesis
In this lesson, students considered two contexts that motivate the need for numbers less than zero. Focus their attention on what zero represents in each situation, since that choice affects the interpretation of positive and negative numbers in the context.
- What does zero represent in each situation? (freezing point of water, sea level)
- What does a positive number represent in each context? (temperatures above freezing, elevations above sea level)
- What does a negative number represent in each context? (temperatures below freezing, elevations below sea level)

- Is -30 degrees warmer or colder than -40 degrees?
- Is an elevation of -20 feet higher or lower than an elevation of -10 feet?
- In general, what is a positive number? Where are they located on a number line? (a number that is greater than zero; on the same side of 0 as 1, which is usually to the right of zero or above zero)
- In general, what is a negative number? Where are they located on a number line? (a number that is less than zero; on the opposite side of 0 as 1, which is usually to the left of zero or below zero)
1.4: Cool-down - Agree or Disagree? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Positive numbers are numbers that are greater than 0. Negative numbers are numbers that are less than zero. The meaning of a negative number in a context depends on the meaning of zero in that context.
For example, if we measure temperatures in degrees Celsius, then 0 degrees Celsius corresponds to the temperature at which water freezes.
In this context, positive temperatures are warmer than the freezing point and negative temperatures are colder than the freezing point. A temperature of -6 degrees Celsius means that it is 6 degrees away from 0 and it is less than 0. This thermometer shows a temperature of -6 degrees Celsius.
If the temperature rises a few degrees and gets very close to 0 degrees without reaching it, the temperature is still a negative number.

Another example is elevation, which is a distance above or below sea level. An elevation of 0 refers to the sea level. Positive elevations are higher than sea level, and negative elevations are lower than sea level.