Lesson 6
Absolute Value of Numbers
6.1: Number Talk: Closer to Zero (5 minutes)
Warm-up
The purpose of this Number Talk is to elicit strategies and understandings students have about the distance from 0 on the number line. These understandings help students develop fluency and will be helpful later in this lesson when students will need to be able to think about distance from 0 for various rational numbers. While four problems are given, it may not be possible to share every strategy. Consider gathering only two or three different strategies per problem.
Launch
Reveal one problem at a time. Give students 30 seconds of quiet think time for each problem and ask them to give a signal when they have an answer and a strategy. Keep all previous problems displayed throughout the talk. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
For each pair of expressions, decide mentally which one has a value that is closer to 0.
\(\frac{9}{11}\) or \(\frac{15}{11}\)
\(\frac15\) or \(\frac19\)
\(1.25\) or \(\frac54\)
\(0.01\) or \(0.001\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their reasoning for each problem. Record and display their explanations for all to see. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone have the same answer but would explain it differently?”
- “Did anyone reason about the problem in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
- “Do you agree or disagree? Why?
Design Principle(s): Optimize output (for explanation)
6.2: Jumping Flea (15 minutes)
Activity
The purpose of this task is to help students understand the absolute value of a number as its distance from 0 on the number line. The context is not realistic, but helps students visualize relationships on the number line in a more concrete way. Students have used the concept of absolute value informally in previous lessons, but this is where the term is formally introduced and used precisely (MP6).
Launch
Allow students 10 minutes quiet work time followed by whole-class discussion.
Students using the digital materials, will use an applet to visualize the bug jumping. Students can pick a starting point for the bug, choose the direction it jumps, and then check where it lands.
Student Facing
Move the bug to a starting point, choose a jump distance, and press the jump button. You may need to zoom in or out if your bug jumps off the screen.
- A bug is jumping around on a number line.
- If the bug starts at 1 and jumps 4 units to the right, where does it end up? How far away from 0 is this?
- If the bug starts at 1 and jumps 4 units to the left, where does it end up? How far away from 0 is this?
- If the bug starts at 0 and jumps 3 units away, where might it land?
- If the bug jumps 7 units and lands at 0, where could it have started?
- The absolute value of a number is the distance it is from 0. The bug is currently to the left of 0 and the absolute value of its location is 4. Where on the number line is it?
- If the bug is to the left of 0 and the absolute value of its location is 5, where on the number line is it?
- If the bug is to the right of 0 and the absolute value of its location is 2.5, where on the number line is it?
- We use the notation \(|{\text-2}|\) to say “the absolute value of -2,” which means “the distance of -2 from 0 on the number line.”
- What does \(|{\text-7}|\) mean and what is its value?
- What does \(|{1.8}|\) mean and what is its value?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Allow students 10 minutes quiet work time followed by whole-class discussion.
Students using the digital materials, will use an applet to visualize the bug jumping. Students can pick a starting point for the bug, choose the direction it jumps, and then check where it lands.
Student Facing
-
A flea is jumping around on a number line.
-
If the flea starts at 1 and jumps 4 units to the right, where does it end up? How far away from 0 is this?
-
If the flea starts at 1 and jumps 4 units to the left, where does it end up? How far away from 0 is this?
-
If the flea starts at 0 and jumps 3 units away, where might it land?
-
If the flea jumps 7 units and lands at 0, where could it have started?
- The absolute value of a number is the distance it is from 0. The flea is currently to the left of 0 and the absolute value of its location is 4. Where on the number line is it?
- If the flea is to the left of 0 and the absolute value of its location is 5, where on the number line is it?
- If the flea is to the right of 0 and the absolute value of its location is 2.5, where on the number line is it?
-
-
We use the notation \(|{\text-2}|\) to say "the absolute value of -2," which means "the distance of -2 from 0 on the number line."
- What does \(|\text-7|\) mean and what is its value?
- What does \(|{1.8}|\) mean and what is its value?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may confuse absolute value with opposites, thinking that absolute value changes the sign of the number. Remind students that absolute value represents the distance of the number from 0 without worrying about the sign or direction. Use some concrete examples: in a board game, 3 moves forward and 3 moves backward both involve 3 jumps but you land in different places; traveling 5 miles east or 5 miles west would put the same number of miles on your car’s odometer, but you end up in different places depending on the direction; earning $10 and spending $10 both involve the amount $10 but in one case you gain it and in the other you lose it. Absolute value is just the amount involved, not including the sign.
Activity Synthesis
Define the absolute value of a number as its distance from 0. Ask students to contrast \(|\text-8|\) and \(|8|\) to come to the conclusion that they have the same value but represent the distance between two distinct points and zero. Also ask for situations where they think the absolute value might be useful (example: your car’s odometer tracks the miles you drove, but if you make a round trip—the same distance in two opposite directions—the difference between where you started and where you ended is zero).
To help clear up misconceptions related to opposites and absolute values, ask:
- “What is the difference between a number’s opposite and a number’s absolute value?” (Opposite is another number on the number line whose distance from zero is the same; absolute value is a number that describes that distance.)
- “Does finding a number’s absolute value always mean changing the sign?” (No, absolute value represents the distance from zero. If the number is positive, the number and its absolute value are the same. If the number is negative, the distance is represented by the number without its negative sign.)
- “If \(n\) is any number that can be positive or negative, what is the sign of the absolute value of \(n\)?”
Supports accessibility for: Visual-spatial processing; Conceptual processing
Design Principle(s): Support sense-making, Cultivate conversation
6.3: Absolute Elevation and Temperature (15 minutes)
Activity
The purpose of this task is for students to develop their understanding of the \(|x|\) notation in familiar contexts. They should build their understanding that \(|x|\) represents the distance from zero to \(x\) and that \(|\text-x|\) and \(|x|\) are equal.
Launch
Allow students 10 minutes quiet work time followed by whole-class discussion.
Student Facing
-
A part of the city of New Orleans is 6 feet below sea level. We can use “-6 feet” to describe its elevation, and “\(|\text-6|\) feet” to describe its vertical distance from sea level. In the context of elevation, what would each of the following numbers describe?
-
25 feet
-
\(|25|\) feet
-
-8 feet
-
\(|\text-8|\) feet
-
-
The elevation of a city is different from sea level by 10 feet. Name the two elevations that the city could have.
-
We write “\(\text-5^\circ \text{C}\)” to describe a temperature that is 5 degrees Celsius below freezing point and “\(5^\circ \text{C}\)” for a temperature that is 5 degrees above freezing. In this context, what do each of the following numbers describe?
-
\(1^\circ \text{C}\)
-
\(\text-4^\circ \text{C}\)
-
\(|12|^\circ \text{C}\)
-
\(|\text-7|^\circ \text{C}\)
-
-
-
Which temperature is colder: \(\text-6^\circ \text{C}\) or \(3^\circ \text{C}\)?
-
Which temperature is closer to freezing temperature: \(\text-6^\circ \text{C}\) or \(3^\circ \text{C}\)?
-
Which temperature has a smaller absolute value? Explain how you know.
-
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
At a certain time, the difference between the temperature in New York City and in Boston was 7 degrees Celsius. The difference between the temperature in Boston and in Chicago was also 7 degrees Celsius. Was the temperature in New York City the same as the temperature in Chicago? Explain your answer.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
To summarize students’ work, consider displaying the following diagram and these four expressions. Give students a minute to study the diagram and match each letter on the diagram to an appropriate expression.
- -4 feet
- \(|{15}|\) feet
- \(|{\text -4}|\) feet
- 15 feet

Supports accessibility for: Conceptual processing; Language; Memory
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, students learned the definition of absolute value and its relationship to rational numbers. Ask students to do the following:
- Order the numbers 1, 3, and 6 from least to greatest. (1, 3, 6.)
- Order \(|1|\), \(|3|\), and \(|6|\) from least to greatest. (\(|1|, |3|, |6|\).)
- Order the numbers -1, -3, and -6 from least to greatest. (-6, -3, -1.)
- Order \(|\text-1|\), \(|\text-3|\), and \(|\text-6|\) from least to greatest. (\(|\text-1|, |\text-3|, |\text-6|\).)
- What do you notice about the order of numbers after taking absolute value? Explain why this happens.
Consider asking students to sketch a number line if they get stuck. Students should see that the order remained the same for the positive numbers but reversed for the negative numbers. They should be able to explain that as numbers move to the left on the number line, their absolute value gets larger because they are further from 0. This realization should help solidify the thinking that has been building for the past several lessons about the ordering and magnitude of rational numbers.
6.4: Cool-down - Greater, Less, the Same (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We compare numbers by comparing their positions on the number line: the one farther to the right is greater; the one farther to the left is less.
Sometimes we wish to compare which one is closer to or farther from 0. For example, we may want to know how far away the temperature is from the freezing point of \(0 ^\circ \text{C}\), regardless of whether it is above or below freezing.
The absolute value of a number tells us its distance from 0.
The absolute value of -4 is 4, because -4 is 4 units to the left of 0. The absolute value of 4 is also 4, because 4 is 4 units to the right of 0. Opposites always have the same absolute value because they both have the same distance from 0.
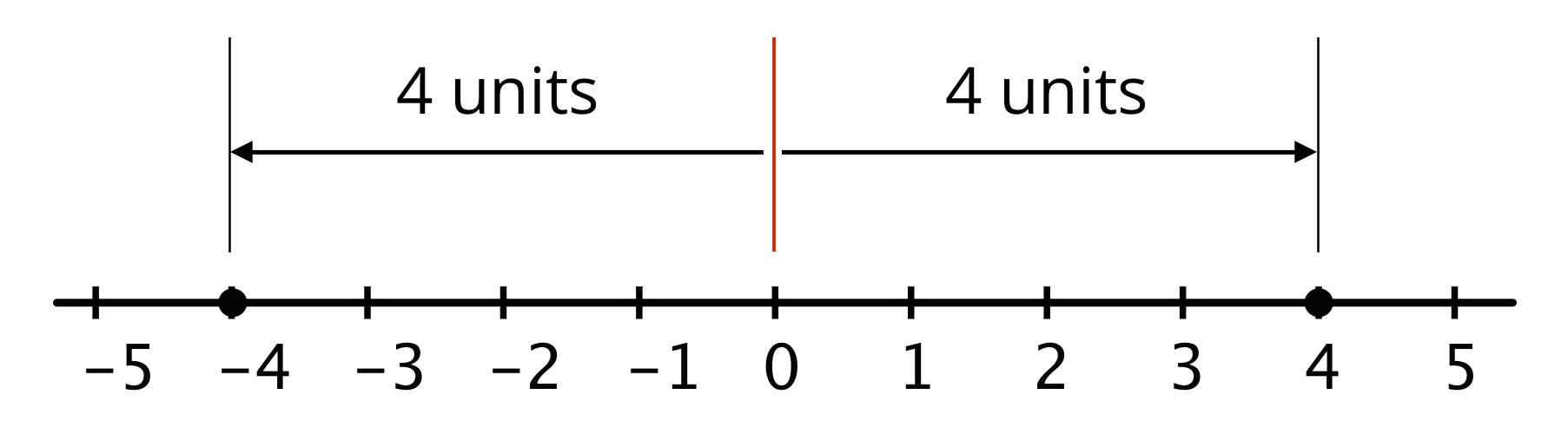
The distance from 0 to itself is 0, so the absolute value of 0 is 0. Zero is the only number whose distance to 0 is 0. For all other absolute values, there are always two numbers—one positive and one negative—that have that distance from 0.
To say “the absolute value of 4,” we write: \(\displaystyle |4|\)
To say that “the absolute value of -8 is 8,” we write: \(\displaystyle |\text- 8| = 8\)