Lesson 3
Comparing Positive and Negative Numbers
3.1: Which One Doesn’t Belong: Inequalities (5 minutes)
Warm-up
This warm-up prompts students to compare four expressions that will prime them for writing inequality statements involving signed numbers in later activities. It encourages students to explain their reasoning, hold mathematical conversations, and gives you the opportunity to hear how they use terminology and talk about characteristics of the inequalities in comparison to one another. To allow all students to access the activity, each inequality has one obvious reason it does not belong. During the discussion, listen for important ideas and terminology that will be helpful in upcoming work of the unit.
At this time, students might explain the direction of the inequality symbol in terms of the size of the numbers. This explanation is acceptable for students to give during this warm-up, but the next activity introduces a more correct concept of ordering that includes negative numbers.
Launch
Arrange students in groups of 2–4. Display the questions for all to see. Ask students to indicate when they have noticed one question that does not belong and can explain why. Give students 1 minute of quiet think time and then time to share their thinking with their group. In their groups, tell each student to share their reasoning why a particular question does not belong and together find at least one reason each question doesn’t belong.
Student Facing
Which inequality doesn’t belong?
- \(\frac{5}{4} < 2\)
- \(8.5 > 0.95\)
- \(8.5 < 7\)
- \(10.00 < 100\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask each group to share one reason why a particular image does not belong. Record and display the responses for all to see. After each response, ask the class if they agree or disagree. Since there is no single correct answer to the question of which one does not belong, attend to students’ explanations and ensure the reasons given are correct. During the discussion, ask students to explain the meaning of any terminology they use, such as “greater than” or “less than.” Also, press students on unsubstantiated claims.
3.2: Comparing Temperatures (10 minutes)
Activity
The purpose of the task is for students to compare signed numbers in a real-world context and then use inequality signs accurately with negative numbers (MP2). The context should help students understand “less than” or “greater than” language. Students evaluate and critique another's reasoning (MP3).
Launch
Allow students 5–6 minutes quiet work time followed by whole-class discussion.
Supports accessibility for: Visual-spatial processing; Organization
Student Facing
Here are the low temperatures, in degrees Celsius, for a week in Anchorage, Alaska.
| day | Mon | Tues | Weds | Thurs | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| temperature | 5 | -1 | -5.5 | -2 | 3 | 4 | 0 |
- Plot the temperatures on a number line. Which day of the week had the lowest low temperature?
-
The lowest temperature ever recorded in the United States was -62 degrees Celsius, in Prospect Creek Camp, Alaska. The average temperature on Mars is about -55 degrees Celsius.
- Which is warmer, the coldest temperature recorded in the USA, or the average temperature on Mars? Explain how you know.
- Write an inequality to show your answer.
-
On a winter day the low temperature in Anchorage, Alaska, was -21 degrees Celsius and the low temperature in Minneapolis, Minnesota, was -14 degrees Celsius.
Jada said, “I know that 14 is less than 21, so -14 is also less than -21. This means that it was colder in Minneapolis than in Anchorage.”
Do you agree? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Another temperature scale frequently used in science is the Kelvin scale. In this scale, 0 is the lowest possible temperature of anything in the universe, and it is -273.15 degrees in the Celsius scale. Each \(1\text{ K}\) is the same as \(1^\circ\text{C}\), so \(10\text{ K}\) is the same as \(\text-263.15^\circ\text{C}\).
- Water boils at \(100^\circ \text{C}\). What is this temperature in \(\text{K}\)?
- Ammonia boils at \(\text-35.5^\circ \text{C}\). What is the boiling point of ammonia in \(\text{K}\)?
- Explain why only positive numbers (and 0) are needed to record temperature in \(\text{K}\).
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty comparing numbers on the negative side of the number line. Have students plot the numbers on a number line in order to sequence them from least to greatest. Make it evident that temperatures become warmer (i.e., greater) as they move from left to right on the number line.
Activity Synthesis
Ask students to explain how they could tell which of the two negative numbers was greater in problem 2. After gathering 1 or 2 responses, display the following image for all to see:
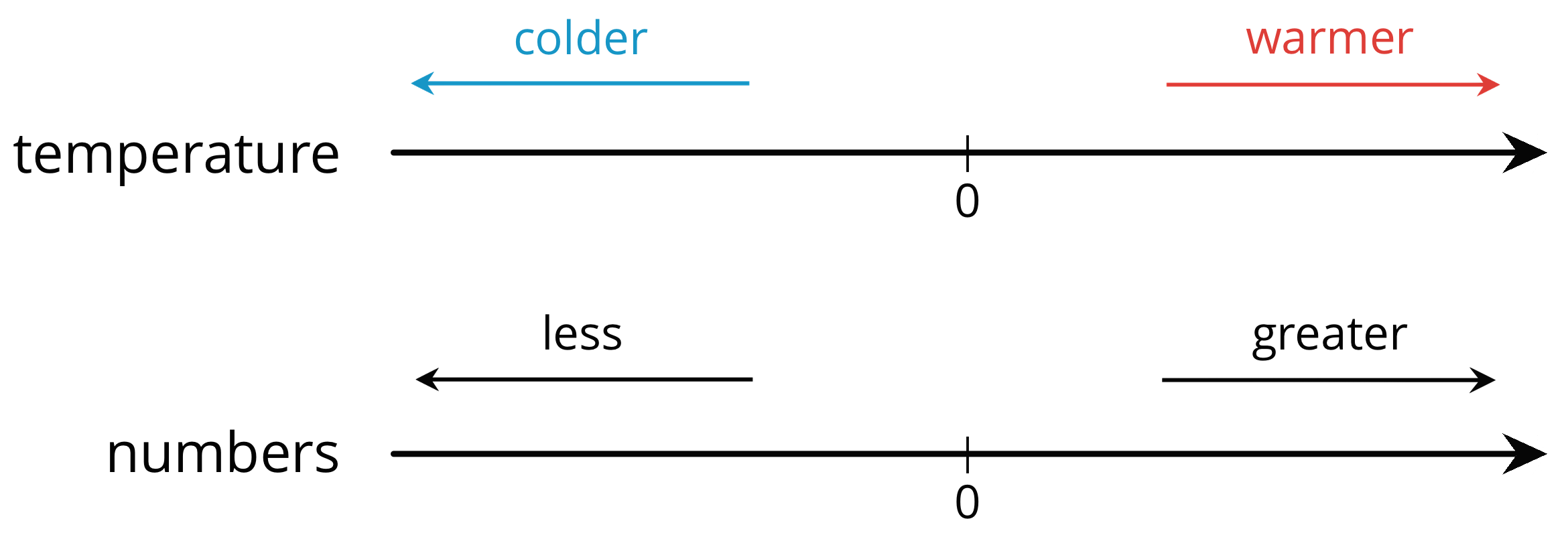
Explain to students that as we go to the right on the number line, we can think of the temperature as getting hotter, and as we go to the left, we can think of the temperature as getting colder. Numbers don’t always describe temperature, though. So we use the word “greater” to describe a number that is farther to the right, and “less” to describe numbers that are farther to the left. For example, we would write \(6 > \text-50\) and say “6 is greater than -50 because it is farther to the right on the number line.” Equivalently, we could write \(\text-50 < 6\) and say “-50 is less than 6 because -50 is farther to the left on the number line.”
Ask students to make up their own list of negative numbers and plot on a number line. Then ask them to write several inequality statements with their numbers. As time allows, have students share one inequality statement with the class to see if all agree that it is true. If time allows, have students swap their list with a partner to plot and check their partner’s number lines and inequality statements.
Design Principle(s): Optimize output (for comparison); Maximize meta-awareness
3.3: Rational Numbers on a Number Line (15 minutes)
Activity
The purpose of this task is for students to understand that for a given number, numbers to the left are always less than the number, and numbers to the right are always greater than the number. The precise use of the term “absolute value” is not expected at this time.
Launch
Allow 10 minutes quiet work time followed by whole-class discussion.
Students using the digital materials can graph the points and check them with the applet. Marks at each half, quarter, and eighth of a unit can be shown to help plot the points or to self-check for accuracy.
Supports accessibility for: Conceptual processing; Organization
Student Facing
-
Plot the numbers -2, 4, -7, and 10 on the number line. Label each point with its numeric value.
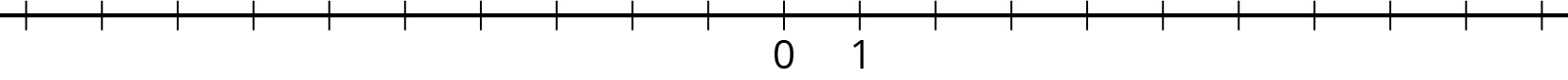
-
Decide whether each inequality statement is true or false. Be prepared to explain your reasoning.
- \(\text-2 < 4\)
- \(\text-2 < \text-7\)
- \(4 > \text-7\)
- \(\text-7 > 10\)
Drag each point to its proper place on the number line. Use your observations to help answer the questions that follow.
-
Andre says that \(\frac14\) is less than \(\text{-}\frac {3}{4}\) because, of the two numbers, \(\frac14\) is closer to 0. Do you agree? Explain your reasoning.
- Answer each question. Be prepared to explain how you know.
-
Which number is greater: \(\frac14\) or \(\frac54\)?
-
Which number is farther from 0: \(\frac14\) or \(\frac54\)?
-
Which number is greater: \(\text{-}\frac {3}{4}\) or \(\frac58\)?
-
Which number is farther from 0: \(\text{-}\frac {3}{4}\) or \(\frac58\)?
-
Is the number that is farther from 0 always the greater number? Explain your reasoning.
-
Student Response
For access, consult one of our IM Certified Partners.
Launch
Allow 10 minutes quiet work time followed by whole-class discussion.
Students using the digital materials can graph the points and check them with the applet. Marks at each half, quarter, and eighth of a unit can be shown to help plot the points or to self-check for accuracy.
Supports accessibility for: Conceptual processing; Organization
Student Facing
-
Plot the numbers -2, 4, -7, and 10 on the number line. Label each point with its numeric value.
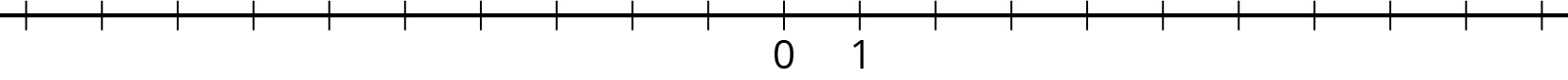
-
Decide whether each inequality statement is true or false. Be prepared to explain your reasoning.
- \(\text-2 < 4\)
- \(\text-2 < \text-7\)
- \(4 > \text-7\)
- \(\text-7 > 10\)
- Andre says that \(\frac14\) is less than \(\text{-}\frac {3}{4}\) because, of the two numbers, \(\frac14\) is closer to 0. Do you agree? Explain your reasoning.
-
Answer each question. Be prepared to explain how you know.
- Which number is greater: \(\frac14\) or \(\frac54\)?
- Which is farther from 0: \(\frac14\) or \(\frac54\)?
- Which number is greater: \(\text{-}\frac {3}{4}\) or \(\frac58\)?
- Which is farther from 0: \(\text{-}\frac {3}{4}\) or \(\frac58\)?
- Is the number that is farther from 0 always the greater number? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty comparing numbers on the negative side of the number line. Have students plot the numbers on a number line from least to greatest. It may be helpful to provide an example that students can use as a visual aid while they are working independently.
Some students may have difficulty comparing fractions in question 4. Remind them that comparing fractions is easier using a common denominator. Suggest that they subdivide the interval from 0 to 1 into fourths or eighths.
Activity Synthesis
The key takeaway from the discussion is that now that we have numbers on both sides of 0, distance from 0 isn’t enough to compare two numbers. Instead, we call numbers farther to the left on the number line “less” and numbers farther to the right “greater.” Display the following number line for all to see:

One inequality at a time, ask students to indicate whether they think each of the following is true or false:
- \(\frac54 > \text{-}\frac {3}{2}\) (true)
- \(\frac54\) is farther from 0 than \(\text{-}\frac {3}{2}\) (false)
- \(\text{-}\frac {3}{2} < \text{-}\frac {3}{4}\) (true)
- \(\text{-}\frac {3}{2}\) is farther from 0 than \(\text{-}\frac {3}{4}\) (true)
Invite students to share their reasoning. Here are some sentence frames that might be helpful:
- “__ is greater (less) than __ because __.”
- “__ is farther from 0 than __ because __.”
Design Principle(s): Optimize output (for explanation); Support sense-making
Lesson Synthesis
Lesson Synthesis
Introduce the word sign to mean whether a number is positive or negative and give a few examples like “The sign of -3 is negative. The sign of 5 is positive.” Explain that 0 has no sign because it is neither positive nor negative. Then display the number line for all to see.
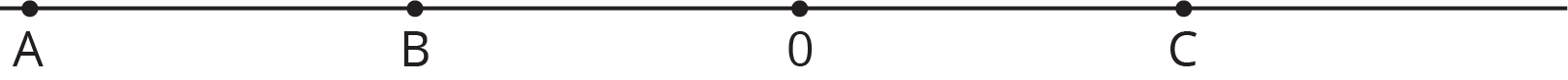
- What is the sign of A? B? C? Which number is closest to 0? (negative; negative; positive; B and C both look equally close but it is hard to be sure)
- Is A greater than B? How can we write an inequality statement comparing A and B? (no; \(A < B\))
- Is A less than C? How can we write an inequality statement comparing A and C? (yes; \(A < C\))
- Is B equal to C? Write a statement that correctly compares B and C. (no, \(B < C\) or \(C > B\))
- If we plot two numbers on the number line, how can we tell which one is greater? (We call the one to the right “greater”)
3.4: Cool-down - Making More Comparisons (10 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We use the words greater than and less than to compare numbers on the number line. For example, the numbers -2.7, 0.8, and -1.3, are shown on the number line.

Because -2.7 is to the left of -1.3, we say that -2.7 is less than -1.3. We write:
\(\displaystyle \text-2.7 <\text -1.3\)
In general, any number that is to the left of a number \(n\) is less than \(n\).
We can see that -1.3 is greater than -2.7 because -1.3 is to the right of -2.7. We write:
\(\displaystyle \text-1.3 >\text -2.7\)
In general, any number that is to the right of a number \(n\) is greater than \(n\)
We can also see that \(0.8 > \text-1.3\) and \(0.8 > \text-2.7\). In general, any positive number is greater than any negative number.