Lesson 2
Points on the Number Line
2.1: A Point on the Number Line (5 minutes)
Warm-up
The purpose of this activity is to prime students for locating negative fractions on a number line. Students discern the value of a number by analyzing its position relative to landmarks on the number line. In this case, students estimate that the point is halfway between 2 and 3 and use their understanding about fractions and decimals to identify numbers equal or close to 2.5. In later activities, students do the same process when describing negative rational numbers, except with those numbers increasing in magnitude going from right to left.
Notice students who argue that 2.49 is correct or incorrect.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet think time and then 2 minutes for partner discussion.
Student Facing
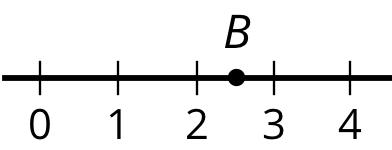
Which of the following numbers could be \(B\)?
2.5
\(\frac25\)
\(\frac{5}{2}\)
\(\frac{25}{10}\)
2.49
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of this discussion is for students to understand that they can use landmarks on the number line (in this case, 2 and 3) and their knowledge of fractions to identify equivalent expressions of a number on the number line. Ask students:
- “Were there any responses you could tell right away were not correct? How?” (Sample response: \(\frac25\) is less than 1, but \(B\) is between 2 and 3.)
- “Were there any responses you had to think harder about? How did you decide those ones?” (Sample response: \(\frac{25}{10}\) seemed too large at first because the numbers are bigger, but after thinking, I saw it is equivalent to \(\frac52\), which I already knew to be correct.)
If time allows, select students to share their thinking about whether 2.49 could represent \(B\).
2.2: What’s the Temperature? (10 minutes)
Activity
The purpose of this task is to use the previously introduced context of temperature to build understanding of the negative side of the number line, both by reading values and assigning values to equally spaced divisions. Non-integer negative numbers are also used. Students reason abstractly and quantitatively as they interpret positive and negative numbers in context (MP2).
Notice the arguments students make to decide whether Elena or Jada are correct in question 2. Some students may defend Elena because they see the liquid is above -2 and conclude that the temperature is -2.5 degrees. Other students will defend Jada by noting the temperature is halfway between -1 and -2 degrees, concluding that it must be -1.5 degrees.
Launch
Allow students 5–6 minutes quiet work time followed by whole-class discussion.
Supports accessibility for: Conceptual processing; Memory
Student Facing
-
Here are five thermometers. The first four thermometers show temperatures in Celsius. Write the temperatures in the blanks.
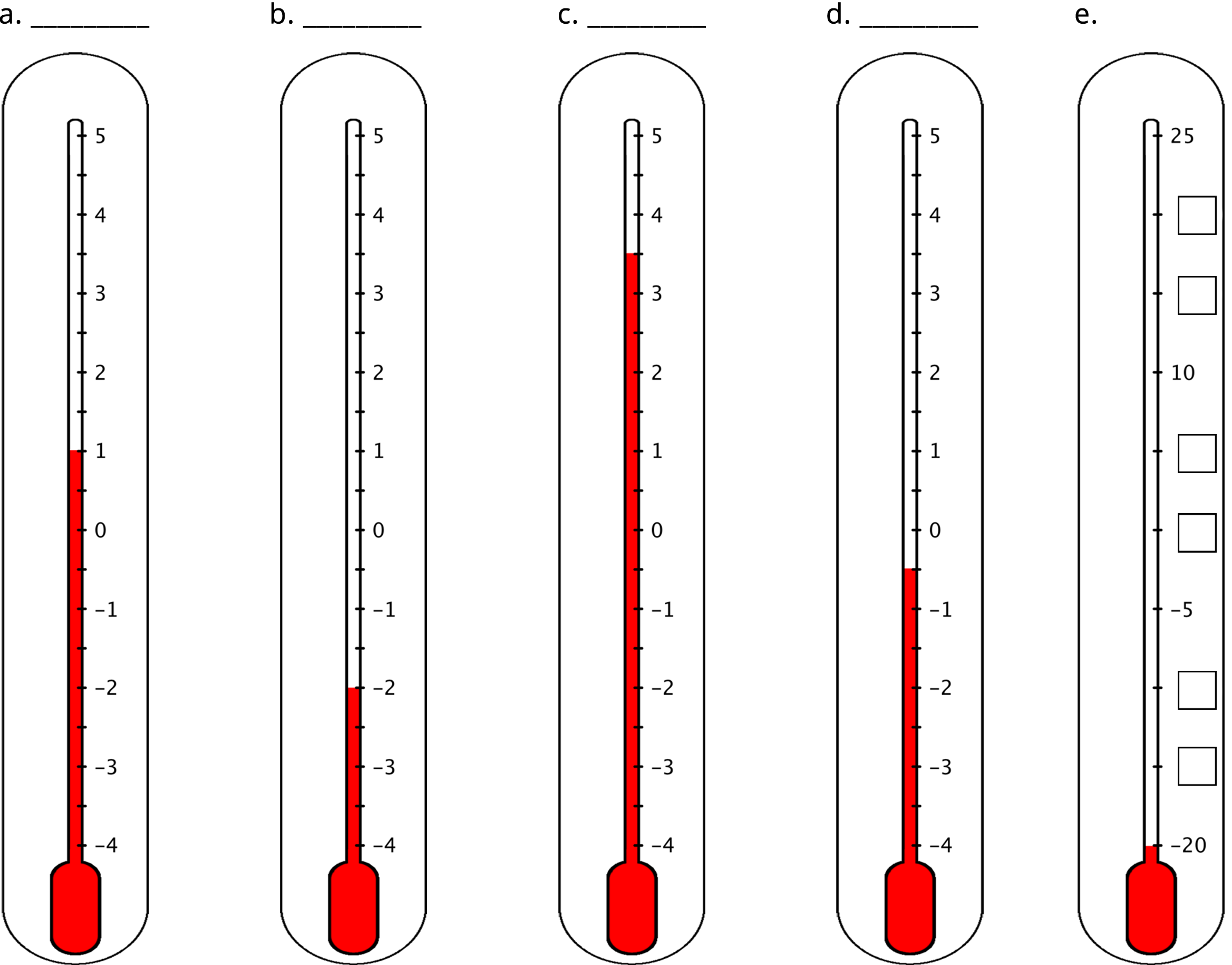
The last thermometer is missing some numbers. Write them in the boxes.
-
Elena says that the thermometer shown here reads \(\text-2.5^\circ \text{C}\) because the line of the liquid is above \(\text-2^\circ \text{C}\). Jada says that it is \(\text-1.5^\circ \text{C}\). Do you agree with either one of them? Explain your reasoning.

- One morning, the temperature in Phoenix, Arizona, was \(8^\circ \text{C}\) and the temperature in Portland, Maine, was \(12^\circ \text{C}\) cooler. What was the temperature in Portland?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty identifying the non-integer temperatures on the thermometers. This difficulty arises when students are unable to identify the scale on a number line. This may be significantly more challenging on the negative side of the number line as students are accustomed to the numbers increasing in magnitude on the positive side as you go up. This issue is addressed in task item number 2. It may be helpful to draw attention to the tick mark between 1 and 2 and its label. This previews the idea of opposites addressed in the next activity.
Activity Synthesis
The purpose of the discussion is to use temperature to explore the concept of negative numbers and introduce the vocabulary of rational numbers. Select students to share their reasoning as to whether they agreed with Jada or Elena in question 2. If not mentioned by students, connect this question to the warm-up by pointing out that the temperature is halfway between -1 and -2 on the number line, and so it must be -1.5 degrees.
Tell students that rational numbers are like fractions except they can also be negative. So rational numbers are all fractions and their opposites. The term “RATIOnal number” comes from the fact that ratios and fractions are closely related ideas. Display some examples of rational numbers like 4, -3.8, \(\text-\frac{4}{3}\), and \(\frac12\) for all to see. Ask students whether they agree 4 and 3.8 are fractions. Tell them these might not look like fractions, but they actually are fractions because they can be written as \(\frac{16}{4}\) and \(\frac{38}{10}\). All rational numbers can be plotted as points on the number line and can be positive, zero, or negative just like temperature.
Design Principle(s): Optimize output (for explanation)
2.3: Folded Number Lines (20 minutes)
Activity
The purpose of this task is both to build an understanding of the symmetry across zero on the number line and to start introducing the notion that we can compare the distance from zero, or the absolute value, of numbers (MP7). Though this activity does not explicitly introduce the vocabulary of absolute value, it seeds the idea that a positive and a negative number can each have the same absolute value.
This is also the first time students work with negative numbers on a horizontal number line. If students have difficulty, remind them of the previous activities where they worked on a vertical number line. It might be helpful to have a vertical number line to display in order to compare and connect.
Launch
Provide access to tracing paper and rulers marked by centimeters. If the tracing paper is less than 20 cm wide, instruct students to make their number lines from -7 to 7 instead of -10 to 10 or instruct them to make their number line on the diagonal of the tracing paper. Allow 10 minutes for students to construct their folded number line and answer question 2. Check student work on question 2 and allow 5 more minutes for all to complete question 3, followed by whole-class discussion.
Supports accessibility for: Visual-spatial processing; Fine-motor skills
Student Facing
Your teacher will give you a sheet of tracing paper on which to draw a number line.
-
Follow the steps to make your own number line.
- Use a straightedge or a ruler to draw a horizontal line. Mark the middle point of the line and label it 0.
- To the right of 0, draw tick marks that are 1 centimeter apart. Label the tick marks 1, 2, 3. . . 10. This represents the positive side of your number line.
- Fold your paper so that a vertical crease goes through 0 and the two sides of the number line match up perfectly.
- Use the fold to help you trace the tick marks that you already drew onto the opposite side of the number line. Unfold and label the tick marks -1, -2, -3. . . -10. This represents the negative side of your number line.
-
Use your number line to answer these questions:
- Which number is the same distance away from zero as is the number 4?
- Which number is the same distance away from zero as is the number -7?
- Two numbers that are the same distance from zero on the number line are called opposites. Find another pair of opposites on the number line.
- Determine how far away the number 5 is from 0. Then, choose a positive number and a negative number that is each farther away from zero than is the number 5.
- Determine how far away the number -2 is from 0. Then, choose a positive number and a negative number that is each farther away from zero than is the number -2.
Pause here so your teacher can review your work.
-
Here is a number line with some points labeled with letters. Determine the location of points \(P\), \(X\), and \(Y\).
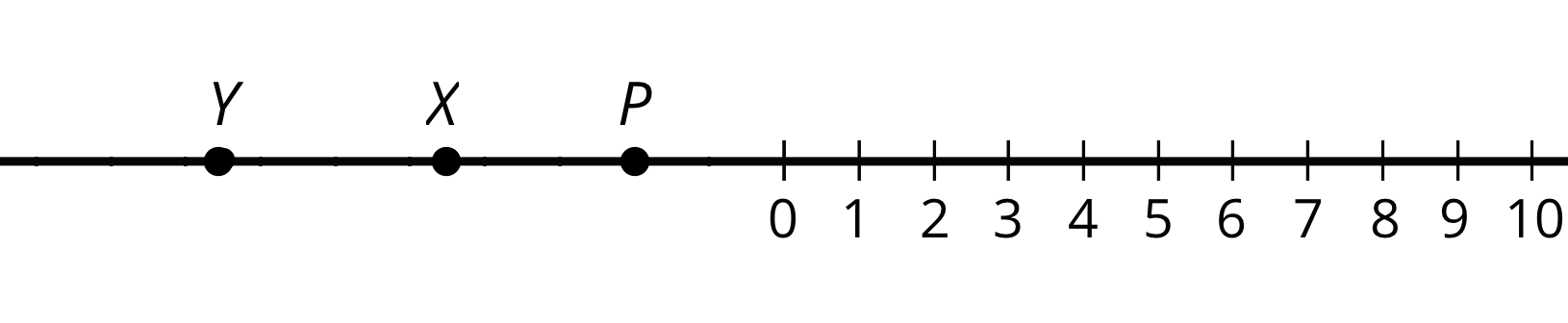
If you get stuck, trace the number line and points onto a sheet of tracing paper, fold it so that a vertical crease goes through 0, and use the folded number line to help you find the unknown values.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
At noon, the temperatures in Portland, Maine, and Phoenix, Arizona, had opposite values. The temperature in Portland was \(18^\circ \text{C}\) lower than in Phoenix. What was the temperature in each city? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty creating a number line. This includes creating equal interval tick marks. Also, students may label the space between the tick marks rather than the tick marks. Have students compare their number line to a peer’s or the previous activities in which a number line was used.
Activity Synthesis
With the new language of opposites, return to the definition of a rational number. We can now think of a rational number as a fraction or the opposite of a fraction. So 6, -6, \(\frac27\), \(\text-\frac27\), 5.8, and -5.8 are all examples of rational numbers. In future grades, students will encounter numbers that are not rational.
The main goal of the discussion is to check that students understand what it means for numbers to be opposites, and to take that a step further in thinking about opposites of opposites. During discussion, it may be useful to provide these sentence frames:
- “The opposite of __ is __.”
- “The opposite of the opposite of __ is __.”
Ask students to identify and name a point on their folded number line and find the opposite of that number. Challenge students to find fractions like \(\frac{5}{2}\) and their opposites on the number line. Then ask them to find the opposite of the opposite. Do this for positive and negative numbers, including numbers written as fractions and decimals. Connect those sentence frames to equations. For example, the opposite of -4 is 4, so \(\text-(\text-4) = 4\). Point out that the opposite of the opposite of a number is always the number itself. We can write, for example, \(\text-(\text-\frac23)=\frac23\) to express that the opposite of the opposite of \(\frac23\) is itself and verify this fact using the number line.
Design Principle(s): Support sense-making; Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
To help students solidify plotting rational numbers in the correct order on both sides of zero and that opposites are the same distance from zero, have them use their folded number lines or draw a new number line to plot some or all of the numbers below:
- Two opposite numbers are 4 units away from each other. What are the numbers? (-2 and 2)
- Two opposite numbers are 7 units away from each other. What are the numbers?(-3.5 and 3.5)
- Two opposite numbers are 10.8 units away from each other. What are the numbers? (-5.4 and 5.4)
- Think about two numbers that are opposites and 106 units away from each other. Describe what they would look like on a large number line. What are the numbers? (Since they are opposites, they are the same distance from 0. So each would be half of 106 units away from 0, which makes the numbers -53 and 53.)
Students should have each successive positive number to the right of the one before it, while the negative numbers move to the left of the one before.
Tell students that they have spent most of their mathematical careers studying positive numbers called fractions. Now that we can find their opposites, we are studying rational numbers, which are fractions and their opposites. The “ratio” in “rational number” comes from the fact that ratios and fractions are closely related.
2.4: Cool-down - Positive, Negative, and Opposite (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here is a number line labeled with positive and negative numbers. The number 4 is positive, so its location is 4 units to the right of 0 on the number line. The number -1.1 is negative, so its location is 1.1 units to the left of 0 on the number line.

We say that the opposite of 8.3 is -8.3, and that the opposite of \(\frac {\text{-}3}{2}\) is \(\frac32\). Any pair of numbers that are equally far from 0 are called opposites.
Points \(A\) and \(B\) are opposites because they are both 2.5 units away from 0, even though \(A\) is to the left of 0 and \(B\) is to the right of 0.
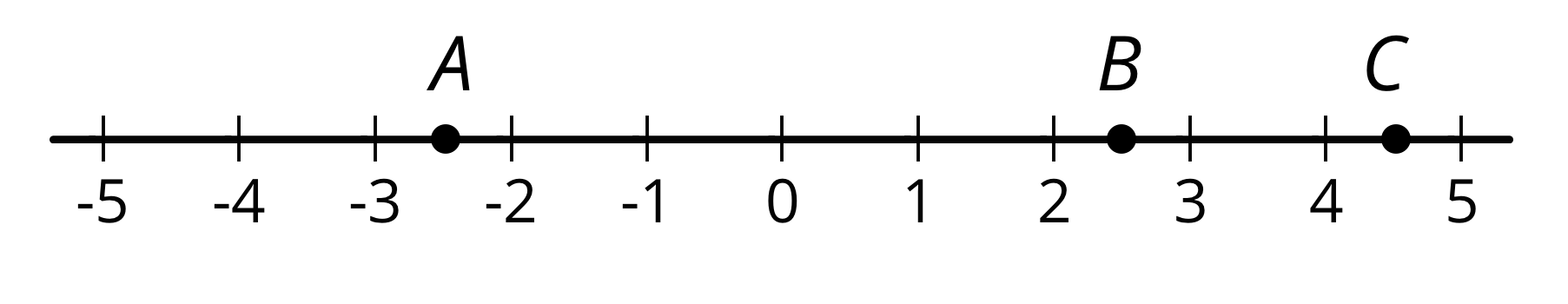
A positive number has a negative number for its opposite. A negative number has a positive number for its opposite. The opposite of 0 is itself.
You have worked with positive numbers for many years. All of the positive numbers you have seen—whole and non-whole numbers—can be thought of as fractions and can be located on a the number line.
To locate a non-whole number on a number line, we can divide the distance between two whole numbers into fractional parts and then count the number of parts. For example, 2.7 can be written as \(2 \frac {7}{10}\). The segment between 2 and 3 can be partitioned into 10 equal parts or 10 tenths. From 2, we can count 7 of the tenths to locate 2.7 on the number line.
All of the fractions and their opposites are what we call rational numbers. For example, 4, -1.1, 8.3, -8.3, \(\frac {\text{-}3}{2}\), and \(\frac32\) are all rational numbers.