Lesson 12
Constructing the Coordinate Plane
12.1: English Winter (5 minutes)
Warm-up
The purpose of this warm-up is for students to reason about the need for quadrants beyond the first quadrant in the coordinate plane when representing data within a situation's context. When choosing an appropriate set of axes, students should also notice that the scale of the axes is important for the given data. Both of these ideas will be important for students' reasoning in upcoming activities.
While option B is the preferred response, it is more important that students explain and support whatever choice they make.
Launch
Give students 2 minutes of quiet work time followed by a whole-class discussion. If needed, clarify that the term "noon" refers to 12 p.m.
Student Facing
The following data were collected over one December afternoon in England.
| time after noon (hours) |
temperature (\(^\circ \text{C}\)) |
|---|---|
| 0 | 5 |
| 1 | 3 |
| 2 | 4 |
| 3 | 2 |
| 4 | 1 |
| 5 | -2 |
| 6 | -3 |
| 7 | -4 |
| 8 | -4 |
- Which set of axes would you choose to represent these data? Explain your reasoning.
- Explain why the other two sets of axes did not seem as appropriate as the one you chose.


Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Poll the class on which set of axes they chose to represent the data. Ask selected students to explain why they chose one set of axes and did not choose the other two. Record and display the responses for all to see. If possible, display and reference the three sets of axes as students explain their reasoning.
If there is time, ask students what kind of data would make the other sets of axes appropriate choices. For example, set A would be appropriate if the temperatures were all positive and set C would be appropriate if the data were collected at 10 hour intervals and happened to be close to multiples of 10.
12.2: Axes Drawing Decisions (25 minutes)
Activity
The purpose of this activity is for students to draw their own axes for different sets of coordinates. They must decide which of the four quadrants they need to use and how to scale the axes. Some students may use logic such as “the largest/smallest point is this, so my axes must go at least that far.” Identify these strategies for the discussion. Monitor for differences in scales and axes where the points were still able to be plotted correctly to highlight during discussion.
Launch
Arrange students in groups of 2. Allow 10 minutes for students to construct their graphs and discuss them with their partners. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Design Principle(s): Maximize meta-awareness
Student Facing
-
Here are three sets of coordinates. For each set, draw and label an appropriate pair of axes and plot the points.
-
\((1, 2), (3, \text-4), (\text-5, \text-2), (0, 2.5)\)

-
\((50, 50), (0, 0), (\text-10, \text-30), (\text-35, 40)\)

-
\(\left(\frac14, \frac34\right), \left(\frac {\text{-}5}{4}, \frac12\right), \left(\text-1\frac14, \frac {\text{-}3}{4}\right), \left(\frac14, \frac {\text{-}1}{2}\right)\)

-
-
Discuss with a partner:
- How are the axes and labels of your three drawings different?
- How did the coordinates affect the way you drew the axes and label the numbers?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Make sure that students label distances on their axes consistently. For example, if the first tick mark after 0 is 3, then the next must be 6 in order for the spacing to be consistent.
Activity Synthesis
The key takeaway from this discussion is that defining axes and scale is a process of reasoning, not an exact science. Ask students to share their strategies about how to place and scale their axes. First, display previously selected student responses that capture the same data on their axes, but with slightly different origins or scales. Ask students which axes they think better represent the data. If not mentioned by students, point out that axes with a lot of empty space probably could benefit from either a different scale or a different origin. Select previously identified students to demonstrate a reliable strategy for finding the needed maximum or minimum. Link back to the warm-up when talking about how to scale the axes: if there are larger numbers, then a bigger scale makes more sense. Also draw attention to the fractional coordinates and how using decimal equivalents might make it easier to scale.
12.3: Positively A-maze-ing (10 minutes)
Optional activity
The purpose of this task is for students to locate and express coordinates in all four quadrants as they navigate around a maze. Students plan their route through the maze and strategically choose coordinates to correctly execute their plans (MP1).
This activity was inspired by one created by Nathan Kraft https://teacher.desmos.com/activitybuilder/custom/563c039dccdd442e107a0ce2.
Launch
Give students 8 minutes quiet work time followed by a brief whole-class discussion.
If using digital materials, students will navigate around a maze using a digital applet.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
Here is a maze on a coordinate plane. The black point in the center is (0, 0). The side of each grid square is 2 units long.
- Enter the above maze at the location marked with a green segment. Draw line segments to show your way through and out of the maze. Label each turning point with a letter. Then, list all the letters and write their coordinates.
- Choose any 2 turning points that share the same line segment. What is the same about their coordinates? Explain why they share that feature.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Give students 8 minutes quiet work time followed by a brief whole-class discussion.
If using digital materials, students will navigate around a maze using a digital applet.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
Here is a maze on a coordinate plane. The black point in the center is (0, 0). The side of each grid square is 2 units long.
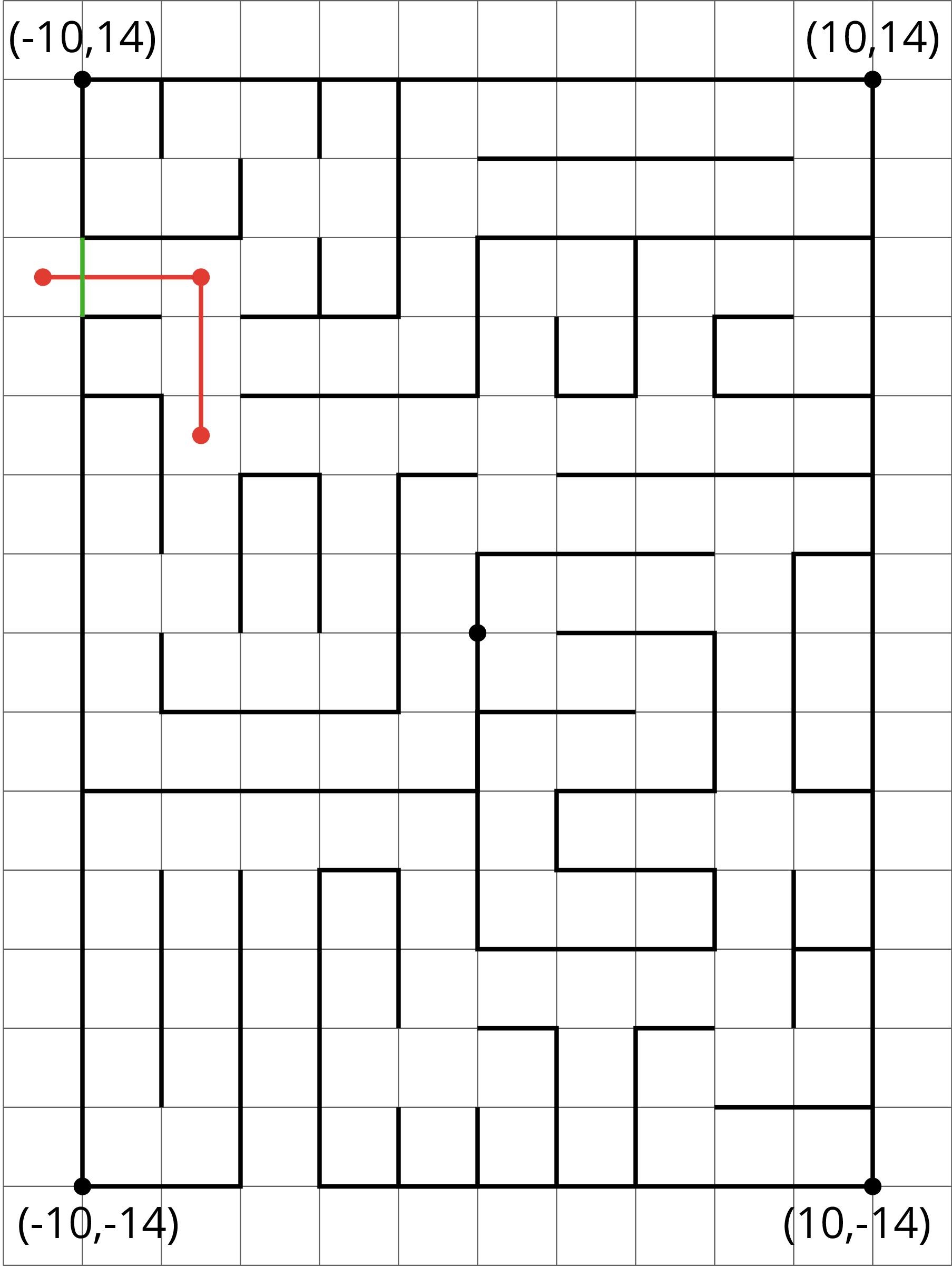
-
Enter the above maze at the location marked with a green segment. Draw line segments to show your way through and out of the maze. Label each turning point with a letter. Then, list all the letters and write their coordinates.
- Choose any 2 turning points that share the same line segment. What is the same about their coordinates? Explain why they share that feature.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
To get from the point \((2,1)\) to \((\text-4,3)\) you can go two units up and six units to the left, for a total distance of eight units. This is called the “taxicab distance,” because a taxi driver would have to drive eight blocks to get between those two points on a map.

Find as many points as you can that have a taxicab distance of eight units away from \((2,1)\). What shape do these points make?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might disregard the fact that the side of each square grid is 2 units and just count boxes. Redirect students' attention to the relevant instruction, and ask how they will address it.
Activity Synthesis
Ask students to share how they planned which points to plot and how they determined the coordinates for each point with the given information. Invite students to share their responses for question 2 to review the idea that points on a horizontal line share the same \(y\)-coordinate and points on the same vertical line share the same \(x\)-coordinate. Explain that in modern navigation, directions are precisely given in terms of coordinates. Navigation programs process coordinate data and translate it into a visual display for the driver, for example. Precise coordinates are also used to navigate through virtual space in computer simulations.
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, students placed and scaled axes to accommodate a variety of points with rational coordinates. To get students thinking about proper scaling, it may be helpful to start with two points plotted with axes that have been scaled improperly. Display an empty grid where both axes are labeled by 100 units from -500 to 500 and attempt to plot the points \((\text-2, 3)\) and \((5, 7)\). Emphasize that it is difficult to communicate information on a coordinate plane if the axes are labeled poorly. Here are some questions to consolidate what students have learned:
- When plotting \((\text-2, 3)\) and \((5, 7)\), how many units across would you make the \(x\)- and \(y\)-axes? How would you label the axes? (The \(x\)-axis needs to be at least 7 units across to go from -2 to 5. The \(y\)-axis needs to include values from 3 to 7, but in order to meet the \(x\)-axis, it should go at least from 0 to 7. It might look nicer to give some space in either direction, for example going from -4 to 7 in the \(x\) direction and -1 to 8 in the \(y\) direction. In this case, the grid lines could be labeled by 1 unit.)
- When plotting \((1.75, \text-0.5)\) and \((\text-2.25, 1.5)\), how many units across would you make the \(x\)- and \(y\)-axes? How would you label the axes? (The coordinates all look like multiples of 0.25, so the grid lines could be labeled by multiples of 0.25 units. The \(x\)-axis could go from -2.5 to 2 and the \(y\)-axis could go from -0.75 to 1.75.)
- When plotting \((\text-3, 40)\) and \((4,\text-60)\), how many units across would you make the \(x\)- and \(y\)-axes? How would you label the axes? (The \(x\) axis could be labeled by 1 unit and the \(y\) axis could be labeled by 10 units. The \(x\)-axis could go from -5 to 5 and the \(y\)-axis could go from -70 to 50.)
It may be helpful to display an empty grid to place and label the axes and plot the points for each example.
12.4: Cool-down - What Went Wrong: Graphing Edition (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The coordinate plane can be used to show information involving pairs of numbers.
When using the coordinate plane, we should pay close attention to what each axis represents and what scale each uses.
Suppose we want to plot the following data about the temperatures in Minneapolis one evening.
| time (hours from midnight) |
temperature (degrees C) |
|---|---|
| -4 | 3 |
| -1 | -2 |
| 0 | -4 |
| 3 | -8 |
We can decide that the \(x\)-axis represents number of hours in relation to midnight and the \(y\)-axis represents temperatures in degrees Celsius.
- In this case, \(x\)-values less than 0 represent hours before midnight, and \(x\)-values greater than 0 represent hours after midnight.
- On the \(y\)-axis, the values represents temperatures above and below the freezing point of 0 degrees Celsius.
The data involve whole numbers, so it is appropriate that the each square on the grid represents a whole number.
- On the left of the origin, the \(x\)-axis needs to go as far as -4 or less (farther to the left). On the right, it needs to go to 3 or greater.
- Below the origin, the \(y\)-axis has to go as far as -8 or lower. Above the origin, it needs to go to 3 or higher.
Here is a graph of the data with the axes labeled appropriately.

On this coordinate plane, a point at \((0, 0)\) would mean a temperature of 0 degrees Celsius at midnight. The point at \((\text-4, 3)\) means a temperature of 3 degrees Celsius at 4 hours before midnight (or 8 p.m.).