Lesson 16
Common Factors
16.1: Figures Made of Squares (5 minutes)
Warm-up
The purpose of this warm-up is for students to notice factors and common factors of 6 and 10 based on rectangles that can be made with the corresponding number of squares. Students may notice that the height of each pair of images changes, but they might not connect this to factors. The whole-class discussion should focus on how the images reflect factors of 6 and 10.
Launch
Tell students you will show them four pairs of images and their job is to find something that is similar and different about the pairs of images. Tell them to give a signal when they have at least one thing that is similar and one thing that is different. Give students 1 minute of quiet think time followed by a whole-class discussion.
Student Facing
How are the pairs of figures alike? How are they different?
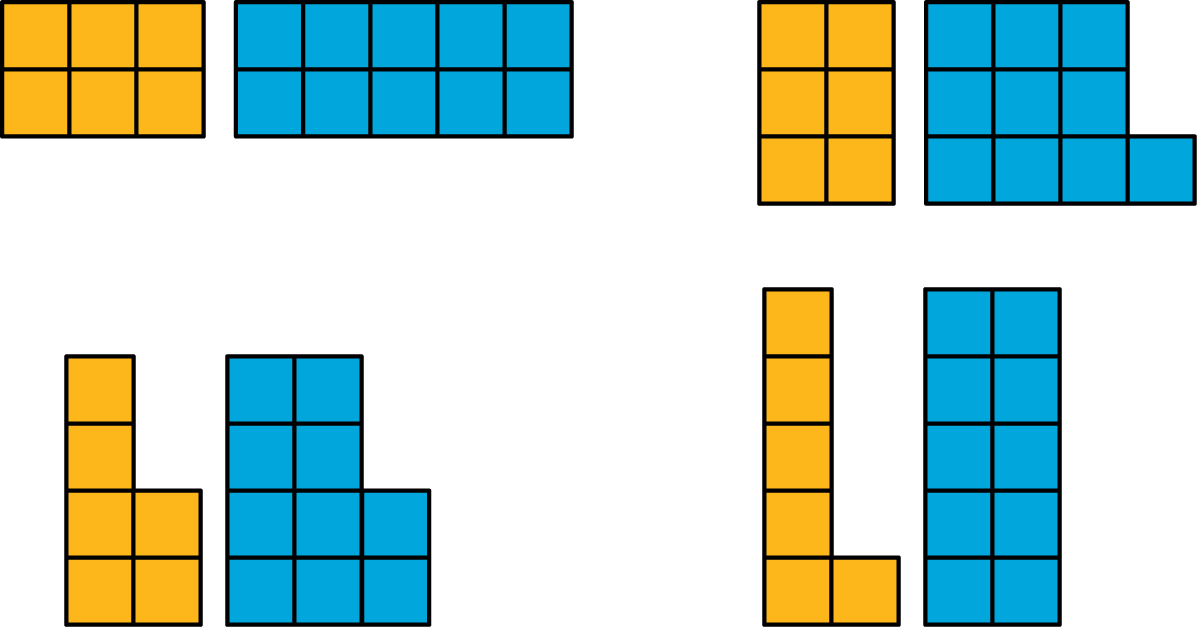
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things that are alike and different among the pairs of images. Record and display their responses for all to see. If possible, reference the images as the students share and record their responses on the images where appropriate.
If the following two ideas do not come up in the conversation, ask students these questions:
- “2 and 3 are both factors of 6. How is this reflected in the diagram?”
- “2 is a factor of both 6 and 10. How is this reflected in the diagram?”
- “4 is not a factor of either 6 or 10. How is this reflected in the diagram?”
End the discussion defining the term factor as one of two or more numbers, that when multiplied together result in a given product. In this particular case, a factor is the height that will make a rectangle have a given area.
16.2: Diego’s Bake Sale (15 minutes)
Activity
Students begin to think about common factors and the greatest common factor in the context of finding ways to group equal amounts of baked goods into bags. Students find all common factors of 2 whole numbers, one representing the number of brownies and another representing cookies. They then compare these factors to determine the greatest common factor.
Monitor for strategies and representations students use to make sure they account for all possible combinations. Some students may organize their work by number of bags, checking each time if the total number can be divided into those bags evenly without remainder. Other students may notice that combinations come in pairs. For example, 4 bags of 12 brownies can be paired with 12 bags of 4 brownies.
Launch
Arrange students in groups of 2. Give students 10 minutes work time followed by whole-class discussion. Encourage students to check in with their partner after each question to make sure they get every possible combination of bags.
Supports accessibility for: Conceptual processing
Design Principle(s): Support sense-making
Student Facing
Diego is preparing brownies and cookies for a bake sale. He would like to make equal-size bags for selling all of the 48 brownies and 64 cookies that he has. Organize your answer to each question so that it can be followed by others.
-
How can Diego package all the 48 brownies so that each bag has the same number of them? How many bags can he make, and how many brownies will be in each bag? Find all the possible ways to package the brownies.
-
How can Diego package all the 64 cookies so that each bag has the same number of them? How many bags can he make, and how many cookies will be in each bag? Find all the possible ways to package the cookies.
- How can Diego package all the 48 brownies and 64 cookies so that each bag has the same combination of items? How many bags can he make, and how many of each will be in each bag? Find all the possible ways to package both items.
- What is the largest number of combination bags that Diego can make with no left over? Explain to your partner how you know that it is the largest possible number of bags.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might not find all combinations of factor pairs for each number. If this is the case, ask them to use snap cubes and prompt them to find more combinations. For example, “Is there a way to place 64 snap cubes into 4 groups with no snap cubes left over? How many are in each group?”
Activity Synthesis
For questions 1 and 2, invite students to share how they organized the different combinations of bags, and highlight their different strategies. Sequence responses by first selecting students who found all combinations using pictorial representations, then students who made an organized list or table, and finally students who were able to highlight the fact that factors come in pairs (i.e. the number of bags and the number of brownies can always be reversed). During this discussion, ask students how they know that they have found all possible bag combinations for each number. Confirm that there should be 10 different bag arrangements for the brownies and 7 different bag arrangements for the chocolate chip cookies.
For questions 3 and 4, ask students to compare answers with a partner. Did they find all the combinations? Confirm that there are 5 different bag arrangements, and the greatest number of bags that can be made is 16. Select a group that used snap cubes to share what this arrangement looks like when represented with the two different colors. If possible, create a visual representation of this arrangement that can be displayed for all to see throughout the rest of the unit.
16.3: Greatest Common Factor (15 minutes)
Activity
In the last activity, students worked with the concept of common factors in the context of distributing two kinds of baked goods equally. In this activity, students explore common factors of numbers more generally and are introduced to the term greatest common factor. The final question connects the concept of greatest common factor to geometry. They describe what the greatest common factor is and how it applies to a geometric context.
Launch
Arrange students in groups of 2. Ask students to discuss what they think a common factor of two numbers is with a partner and select for 1--2 groups to share their thinking. Give 10 minutes of quiet work time followed by whole-class discussion.
Supports accessibility for: Organization; Attention
Design Principle(s): Cultivate conversation; Support sense-making
Student Facing
- The greatest common factor of 30 and 18 is 6. What do you think the term “greatest common factor” means?
- Find all of the factors of 21 and 6. Then, identify the greatest common factor of 21 and 6.
- Find all of the factors of 28 and 12. Then, identify the greatest common factor of 28 and 12.
-
A rectangular bulletin board is 12 inches tall and 27 inches wide. Elena plans to cover it with squares of colored paper that are all the same size. The paper squares come in different sizes; all of them have whole-number inches for their side lengths.
-
What is the side length of the largest square that Elena could use to cover the bulletin board completely without gaps and overlaps? Explain or show your reasoning.
- How is the solution to this problem related to greatest common factor?
-
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A school has 1,000 lockers, all lined up in a hallway. Each locker is closed. Then . . .
- One student goes down the hall and opens each locker.
- A second student goes down the hall and closes every second locker: lockers 2, 4, 6, and so on.
- A third student goes down the hall and changes every third locker. If a locker is open, he closes it. If a locker is closed, he opens it.
- A fourth student goes down the hall and changes every fourth locker.
This process continues up to the thousandth student! At the end of the process, which lockers will be open? (Hint: you may want to try this problem with a smaller number of lockers first.)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not list all of the factors of a number. Prompt these students to try to find more factors. If additional support is needed, provide graph paper and ask the student if it's possible to make a rectangle area equal to the number with a height of 1, 2, 3, 4, etc. until they are convinced they have all the factors.
Activity Synthesis
Ask students to share their thinking to question 4. Record and display their responses for all to see. Consider asking how their responses would change if the bulletin board was 18 inches tall and 63 inches wide instead. Encourage students to use the terms “common factor” and “greatest common factor” in their explanations.
Lesson Synthesis
Lesson Synthesis
In this lesson, students learned about common factors of 2 whole numbers, as well as the greatest common factor. Discuss:
- “What are some situations when finding greatest common factor is helpful?” (When forming the largest amount of equal mixed groups with no items left over, or when determining the largest side length of a square that can be used to tile a rectangle)
- “Explain what greatest common factor means.” (It is the largest factor that numbers share.)
- “How can we can determine the greatest common factor?” (List the factors of each number, circle the ones that are the same, and then find the largest number that is the same.)
16.4: Cool-down - In Your Own Words (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A factor of a whole number \(n\) is a whole number that divides \(n\) evenly without a remainder. For example, 1, 2, 3, 4, 6, and 12 are all factors of 12 because each of them divides 12 evenly and without a remainder.
A common factor of two whole numbers is a factor that they have in common. For example, 1, 3, 5, and 15 are factors of 45; they are also factors of 60. We call 1, 3, 5, and 15 common factors of 45 and 60.
The greatest common factor (sometimes written as GCF) of two whole numbers is the greatest of all of the common factors. For example, 15 is the greatest common factor for 45 and 60.
One way to find the greatest common factor of two whole numbers is to list all of the factors for each, and then look for the greatest factor they have in common. Let’s try to find the greatest common factor of 18 and 24. First, we list all the factors of each number.
-
Factors of 18: 1, 2, 3, 6, 9,18
-
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors are 1, 2, 3, and 6. Of these, 6 is the greatest one, so 6 is the greatest common factor of 18 and 24.