Lesson 4
Ordering Rational Numbers
4.1: How Do They Compare? (10 minutes)
Warm-up
The purpose of this warm-up is for students to review strategies for comparing whole numbers, decimal numbers, and fractions as well as the use of inequality symbols. The numbers in each pair have been purposefully chosen based on misunderstandings students typically have when comparing. Since there are many pairs of numbers to compare, it may not be possible to share all of the students’ strategies for each pair. Consider sharing only one strategy for each pair if all of the students agree and more than one if there is a disagreement among the students.
Launch
Give students 3 minutes of quiet work time followed by a whole-class discussion.
Student Facing
Use the symbols >, <, or = to compare each pair of numbers. Be prepared to explain your reasoning.
- 12 _____ 19
- 212 _____ 190
- 15 _____ 1.5
- 9.02 _____ 9.2
- 6.050 _____ 6.05
- 0.4 _____ \(\frac{9}{40}\)
- \(\frac{19}{24}\) _____ \(\frac{19}{21}\)
- \(\frac{16}{17}\) _____ \(\frac{11}{12}\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not remember the inequality symbols that represent the phrases: greater than, less than, and equal to. Show these students each of the inequality symbols in an example that they can refer back to as they work.
Activity Synthesis
For each pair of numbers, ask one or two students to share their reasoning. Record and display their reasoning for all to see. If the whole class agrees, move on to the next question, but if there is a disagreement, ask students to explain their thinking until an agreement is reached. If possible, spend more time on the questions with numbers expressed with decimals and fractions.
4.2: Ordering Rational Number Cards (15 minutes)
Activity
In this activity, students order rational numbers from least to greatest in 2 steps. They first order positive rational numbers, and then negative ones. The numbers are written as fractions, decimals, and integers. By manipulating physical cards, students get a tangible sense of how rational numbers relate to each other.
Notice conversations students have when deciding how to place fractions and decimals, especially on the negative side of the number line. Pay attention to proper use and understanding of “less” or “greater,” and improper use of “bigger” or “smaller.” One strategy to look for is fitting new numbers between known numbers (e.g., \(\text-\frac98\) is between -1 and -2).
Launch
Arrange students in groups of 2. Distribute the first set of cards to each group. Give students 5 minutes to order the first set of cards, taking turns to place each number. When a group finishes ordering, check their ordering before giving them the second set of cards. To speed up the checking process, consider referring groups finishing the first set to compare their ordering to a group you have already checked. Give students 5 minutes to order the second set of cards followed by whole-class discussion. When collecting the cards, ask groups to separate the negative set of numbers and randomize each set for the next class.
Supports accessibility for: Conceptual processing; Organization
Student Facing
Your teacher will give you a set of number cards. Order them from least to greatest.
Your teacher will give you a second set of number cards. Add these to the correct places in the ordered set.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may place negative numbers in order of increasing absolute value on the left side of 0. Ask these students to draw a number line that goes 5 units right and 5 units left of 0. Point out that negative numbers progress as -1, -2, -3, -4, -5 as they move outward from 0.
Activity Synthesis
The purpose of the discussion is to solidify students’ understanding of the order of rational numbers. Select previously identified students to share how they decided how to place numbers like \(\text-\frac98\), \(\frac98\), \(\frac83\), and \(\text-22\frac12\). Here are some questions to consider:
- Which numbers were hardest to place and which were the least difficult?
- How does placing negative numbers compare to placing positive numbers?
- How did you use numbers you had already placed to reason about where to place new numbers?
Design Principle(s): Support sense-making
4.3: Comparing Points on A Line (15 minutes)
Activity
Students practice using relational language “greater than” and “less than” to describe order and position on number line.
Launch
Arrange students in groups of 2. Give students 7 minutes of quiet work time for both problems before 3–5 minutes for partner discussion, followed by whole-class discussion.
Supports accessibility for: Visual-spatial processing; Organization
Design Principle(s): Optimize output (for justification)
Student Facing
-
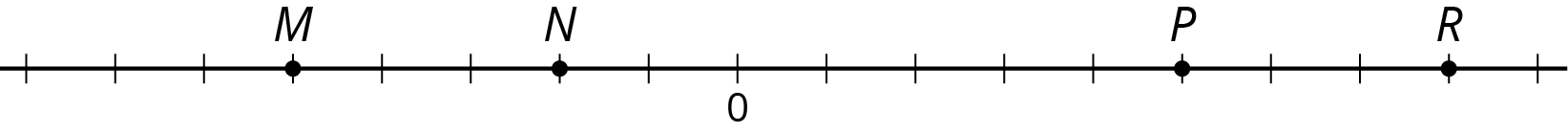
Use each of the following terms at least once to describe or compare the values of points \(M\), \(N\), \(P\), \(R\).
- greater than
- less than
- opposite of (or opposites)
- negative number
-
Tell what the value of each point would be if:
- \(P\) is \(2\frac12\)
- \(N\) is -0.4
- \(R\) is 200
- \(M\) is -15
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The list of fractions between 0 and 1 with denominators between 1 and 3 looks like this:
\( \frac{0}{1}, \, \frac{1}{1},\, \frac{1}{2},\, \frac{1}{3},\, \frac{2}{3}\)
We can put them in order like this: \( \frac{0}{1} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{1}{1}\)
Now let’s expand the list to include fractions with denominators of 4. We won’t include \(\frac{2}{4}\), because \(\frac{1}{2}\) is already on the list.
\( \frac{0}{1} <\frac{1}{4} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{1}{1}\)
- Expand the list again to include fractions that have denominators of 5.
- Expand the list you made to include fractions have have denominators of 6.
- When you add a new fraction to the list, you put it in between two “neighbors.” Go back and look at your work. Do you see a relationship between a new fraction and its two neighbors?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose for discussion is to give students the opportunity to use precise language as they compare the relative positions of rational numbers. Give students 3–5 minutes to discuss their responses with a partner before whole-class discussion. Ask students to share their partner’s reasoning, especially if it was different than their own. Here are some questions to consider for whole-class discussion:
- “Did you ever have a different answer than your partner? If so, were you both correct? If not, how did you work to reach agreement?”
- “How did your partner decide the value of each unit on the number line in problem 2? Did you think of it a different way?”
- “How can we tell if two numbers are opposites?” (They are the same distance from 0.)
- “How can we tell if one number is greater or less than another number?” (Numbers toward the right are considered greater, and numbers toward the left are considered less.)
Lesson Synthesis
Lesson Synthesis
Ask students to summarize the ideas they have developed in the last few lessons about plotting and comparing rational numbers. Here are some questions to consider:
- “What are some situations where negative numbers make sense? What do the words ‘positive,’ ‘negative,’ and 0 mean in those situations?” (Elevation: 0 represents sea level, negative represents below sea level, and positive represents above sea level. Temperature: \(0^\circ \text{C}\) represents the standard freezing point of water, positive represents temperatures warmer than freezing, and negative represents temperatures below freezing.)
- “What about on the number line? What do ‘positive’ and ‘negative’ mean on the number line? Is 0 positive or negative?” (Negative numbers are numbers left of 0 on the number line, and positive numbers are to the right of 0. The number 0 is neither positive nor negative.)
- “What are some ideas you have about ‘opposites?’ What is the opposite of 0?” (Opposites are numbers that are the same distance from 0. They come in pairs—one positive, one negative—except for 0, which is its own opposite.)
- “How can you tell if one number is greater than or less than another? How do you write it?” (Given two rational numbers, the number toward the right on the number line is considered “greater,” and the number toward the left is considered “less.” We use the \(<\) and \(>\) symbols to indicate “less than” and “greater than,” respectively.)
4.4: Cool-down - Getting Them in Order (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
To order rational numbers from least to greatest, we list them in the order they appear on the number line from left to right. For example, we can see that the numbers
-2.7, -1.3, 0.8
are listed from least to greatest because of the order they appear on the number line.
