Lesson 4

Ordering Rational Numbers

Let’s order rational numbers.

4.1: How Do They Compare?

Use the symbols >, <, or = to compare each pair of numbers. Be prepared to explain your reasoning.

  • 12 _____ 19
  • 212 _____ 190
  • 15 _____ 1.5
  • 9.02 _____ 9.2
  • 6.050 _____ 6.05
  • 0.4 _____ \(\frac{9}{40}\)
  • \(\frac{19}{24}\) _____ \(\frac{19}{21}\)
  • \(\frac{16}{17}\) _____ \(\frac{11}{12}\)

4.2: Ordering Rational Number Cards

Your teacher will give you a set of number cards. Order them from least to greatest.

Your teacher will give you a second set of number cards. Add these to the correct places in the ordered set.

4.3: Comparing Points on A Line

  1.  
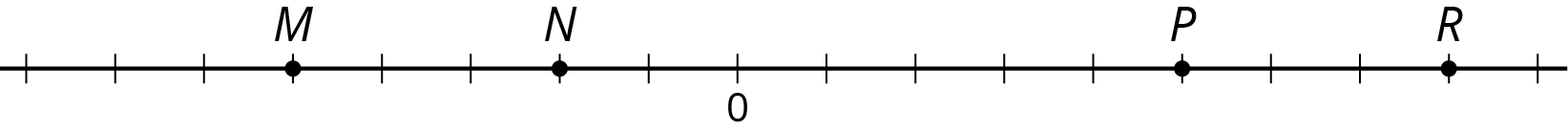
    Number line, evenly spaced tick marks labeled blank, blank, blank, M, blank, blank, N, blank, 0, blank, blank, blank, blank, P, blank, blank, R, blank.

    Use each of the following terms at least once to describe or compare the values of points \(M\), \(N\), \(P\), \(R\).

    • greater than
    • less than
    • opposite of (or opposites)
    • negative number

  2. Tell what the value of each point would be if:

    1. \(P\) is \(2\frac12\)
    2. \(N\) is -0.4
    3. \(R\) is 200
    4. \(M\) is -15


The list of fractions between 0 and 1 with denominators between 1 and 3 looks like this:

\( \frac{0}{1}, \, \frac{1}{1},\, \frac{1}{2},\, \frac{1}{3},\, \frac{2}{3}\)

We can put them in order like this: \( \frac{0}{1} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{1}{1}\)

Now let’s expand the list to include fractions with denominators of 4. We won’t include \(\frac{2}{4}\), because \(\frac{1}{2}\) is already on the list.

\( \frac{0}{1} <\frac{1}{4} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{1}{1}\)

  1. Expand the list again to include fractions that have denominators of 5.
  2. Expand the list you made to include fractions have have denominators of 6.
  3. When you add a new fraction to the list, you put it in between two “neighbors.” Go back and look at your work. Do you see a relationship between a new fraction and its two neighbors?

Summary

To order rational numbers from least to greatest, we list them in the order they appear on the number line from left to right. For example, we can see that the numbers

-2.7, -1.3, 0.8

are listed from least to greatest because of the order they appear on the number line.

Number line, negative 3 to 3 by ones. Above the line, points are indicated at negative 2 point 7, negative 1 point 3, zero point 8.

Glossary Entries

  • negative number

    A negative number is a number that is less than zero. On a horizontal number line, negative numbers are usually shown to the left of 0.

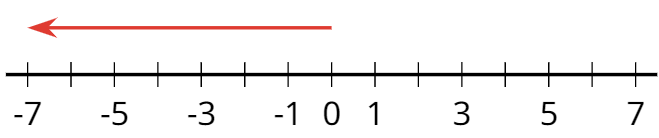
    number line with arrow that extends from 0 to -7
  • opposite

    Two numbers are opposites if they are the same distance from 0 and on different sides of the number line.

    For example, 4 is the opposite of -4, and -4 is the opposite of 4. They are both the same distance from 0. One is negative, and the other is positive.

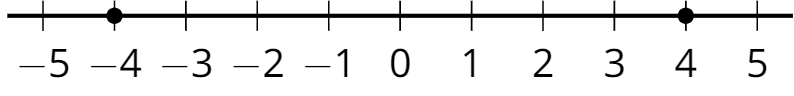
    Number line that extends from -5 to 5, with points at -4 and 4.
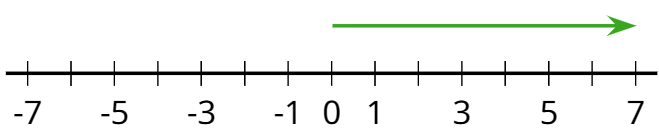
  • positive number

    A positive number is a number that is greater than zero. On a horizontal number line, positive numbers are usually shown to the right of 0.

    Number line with green arrow extending from 0 to 7
  • rational number

    A rational number is a fraction or the opposite of a fraction.

    For example, 8 and -8 are rational numbers because they can be written as \(\frac81\) and \(\text-\frac81\).

    Also, 0.75 and -0.75 are rational numbers because they can be written as \(\frac{75}{100}\) and \(\text-\frac{75}{100}\).

  • sign

    The sign of any number other than 0 is either positive or negative.

    For example, the sign of 6 is positive. The sign of -6 is negative. Zero does not have a sign, because it is not positive or negative.