Lesson 3

Comparing Positive and Negative Numbers

Let’s compare numbers on the number line.

3.1: Which One Doesn’t Belong: Inequalities

Which inequality doesn’t belong?

  • \(\frac{5}{4} < 2\)
  • \(8.5 > 0.95\)
  • \(8.5 < 7\)
  • \(10.00 < 100\)

 

3.2: Comparing Temperatures

Here are the low temperatures, in degrees Celsius, for a week in Anchorage, Alaska.

day Mon Tues Weds Thurs Fri Sat Sun
temperature 5 -1 -5.5 -2 3 4 0
  1. Plot the temperatures on a number line. Which day of the week had the lowest low temperature?

  2. The lowest temperature ever recorded in the United States was -62 degrees Celsius, in Prospect Creek Camp, Alaska. The average temperature on Mars is about -55 degrees Celsius.

    1. Which is warmer, the coldest temperature recorded in the USA, or the average temperature on Mars? Explain how you know.
    2. Write an inequality to show your answer.

  3. On a winter day the low temperature in Anchorage, Alaska, was -21 degrees Celsius and the low temperature in Minneapolis, Minnesota, was -14 degrees Celsius.

    Jada said, “I know that 14 is less than 21, so -14 is also less than -21. This means that it was colder in Minneapolis than in Anchorage.”

    Do you agree? Explain your reasoning.



Another temperature scale frequently used in science is the Kelvin scale. In this scale, 0 is the lowest possible temperature of anything in the universe, and it is -273.15 degrees in the Celsius scale. Each \(1\text{ K}\) is the same as \(1^\circ\text{C}\), so \(10\text{ K}\) is the same as \(\text-263.15^\circ\text{C}\).

  1. Water boils at \(100^\circ \text{C}\). What is this temperature in \(\text{K}\)?
  2. Ammonia boils at \(\text-35.5^\circ \text{C}\). What is the boiling point of ammonia in \(\text{K}\)?
  3. Explain why only positive numbers (and 0) are needed to record temperature in \(\text{K}\).

3.3: Rational Numbers on a Number Line

  1. Plot the numbers -2, 4, -7, and 10 on the number line. Label each point with its numeric value.

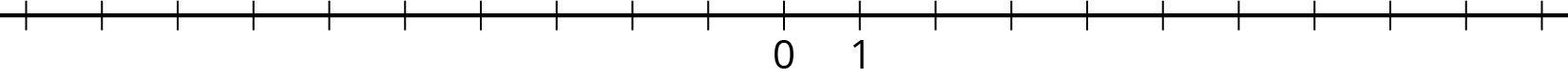
    Number line, 21 evenly spaced tick marks, middle tick mark labeled 0, next labeled 1, the rest blank.

  2. Decide whether each inequality statement is true or false. Be prepared to explain your reasoning.

    1. \(\text-2 < 4\)
    2. \(\text-2 < \text-7\)
    3. \(4 > \text-7\)
    4. \(\text-7 > 10\)

    Drag each point to its proper place on the number line. Use your observations to help answer the questions that follow.

  3. Andre says that \(\frac14\) is less than \(\text{-}\frac {3}{4}\) because, of the two numbers, \(\frac14\) is closer to 0. Do you agree? Explain your reasoning.

  4. Answer each question. Be prepared to explain how you know.

    1. Which number is greater: \(\frac14\) or \(\frac54\)?

    2. Which number is farther from 0: \(\frac14\) or \(\frac54\)?

    3. Which number is greater: \(\text{-}\frac {3}{4}\) or \(\frac58\)?

    4. Which number is farther from 0: \(\text{-}\frac {3}{4}\) or \(\frac58\)?

    5. Is the number that is farther from 0 always the greater number? Explain your reasoning.

Summary

We use the words greater than and less than to compare numbers on the number line. For example, the numbers -2.7, 0.8, and -1.3, are shown on the number line.

Number line, negative 3 to 3 by ones. Above the line, points are indicated at negative 2 point 7, negative 1 point 3, zero point 8.

Because -2.7 is to the left of -1.3, we say that -2.7 is less than -1.3. We write:

\(\displaystyle \text-2.7 <\text -1.3\)

In general, any number that is to the left of a number \(n\) is less than \(n\).

We can see that -1.3 is greater than -2.7 because -1.3 is to the right of -2.7. We write:

\(\displaystyle \text-1.3 >\text -2.7\)

In general, any number that is to the right of a number \(n\) is greater than \(n\)

We can also see that \(0.8 > \text-1.3\) and \(0.8 > \text-2.7\). In general, any positive number is greater than any negative number.

Glossary Entries

  • negative number

    A negative number is a number that is less than zero. On a horizontal number line, negative numbers are usually shown to the left of 0.

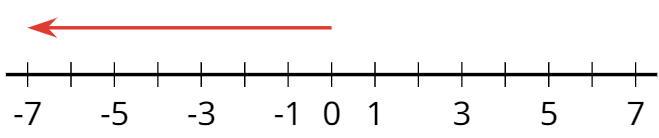
    number line with arrow that extends from 0 to -7
  • opposite

    Two numbers are opposites if they are the same distance from 0 and on different sides of the number line.

    For example, 4 is the opposite of -4, and -4 is the opposite of 4. They are both the same distance from 0. One is negative, and the other is positive.

    Number line that extends from -5 to 5, with points at -4 and 4.
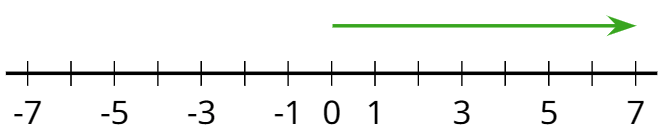
  • positive number

    A positive number is a number that is greater than zero. On a horizontal number line, positive numbers are usually shown to the right of 0.

    Number line with green arrow extending from 0 to 7
  • rational number

    A rational number is a fraction or the opposite of a fraction.

    For example, 8 and -8 are rational numbers because they can be written as \(\frac81\) and \(\text-\frac81\).

    Also, 0.75 and -0.75 are rational numbers because they can be written as \(\frac{75}{100}\) and \(\text-\frac{75}{100}\).

  • sign

    The sign of any number other than 0 is either positive or negative.

    For example, the sign of 6 is positive. The sign of -6 is negative. Zero does not have a sign, because it is not positive or negative.