Lesson 16

Common Factors

Let’s use factors to solve problems.

16.1: Figures Made of Squares

How are the pairs of figures alike? How are they different?

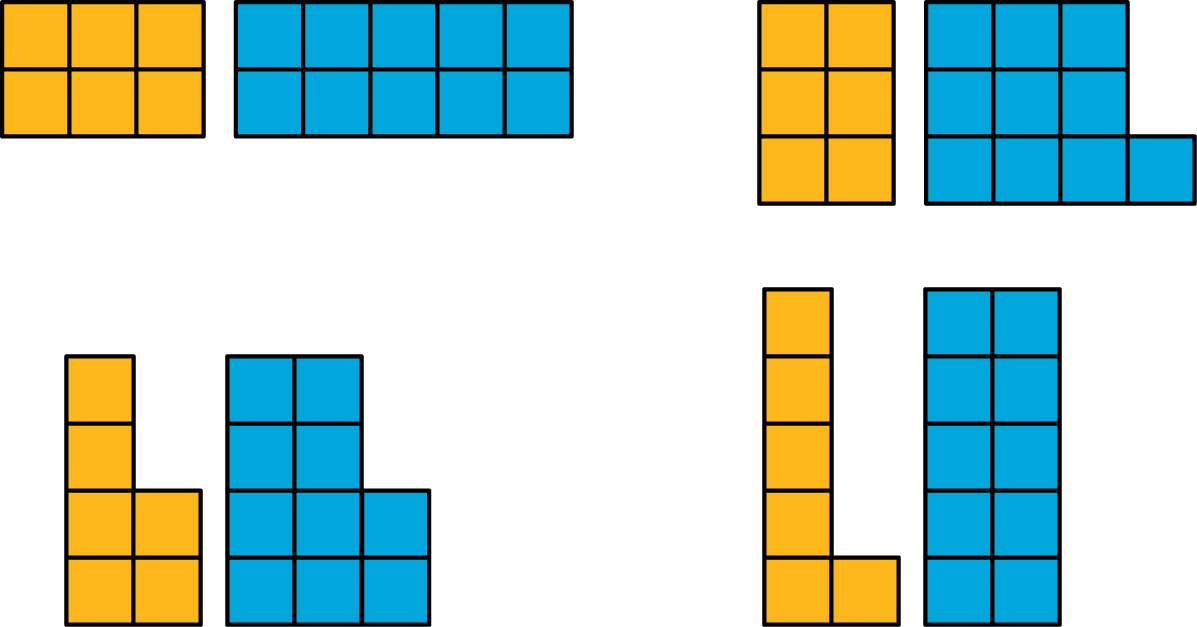
A collection of colored squares, arranged various way.  Please ask for additional help.

 

16.2: Diego’s Bake Sale

Diego is preparing brownies and cookies for a bake sale. He would like to make equal-size bags for selling all of the 48 brownies and 64 cookies that he has. Organize your answer to each question so that it can be followed by others.

  1. How can Diego package all the 48 brownies so that each bag has the same number of them? How many bags can he make, and how many brownies will be in each bag? Find all the possible ways to package the brownies. 

  2. How can Diego package all the 64 cookies so that each bag has the same number of them? How many bags can he make, and how many cookies will be in each bag? Find all the possible ways to package the cookies. 

  3. How can Diego package all the 48 brownies and 64 cookies so that each bag has the same combination of items? How many bags can he make, and how many of each will be in each bag? Find all the possible ways to package both items. 
  4. What is the largest number of combination bags that Diego can make with no left over? Explain to your partner how you know that it is the largest possible number of bags.

16.3: Greatest Common Factor

  1. The greatest common factor of 30 and 18 is 6. What do you think the term “greatest common factor” means?
  2. Find all of the factors of 21 and 6. Then, identify the greatest common factor of 21 and 6.
  3. Find all of the factors of 28 and 12. Then, identify the greatest common factor of 28 and 12.

  4. A rectangular bulletin board is 12 inches tall and 27 inches wide. Elena plans to cover it with squares of colored paper that are all the same size. The paper squares come in different sizes; all of them have whole-number inches for their side lengths.

    1. What is the side length of the largest square that Elena could use to cover the bulletin board completely without gaps and overlaps? Explain or show your reasoning.

    2. How is the solution to this problem related to greatest common factor?


A school has 1,000 lockers, all lined up in a hallway. Each locker is closed. Then . . .

  • One student goes down the hall and opens each locker.
  • A second student goes down the hall and closes every second locker: lockers 2, 4, 6, and so on.
  • A third student goes down the hall and changes every third locker. If a locker is open, he closes it. If a locker is closed, he opens it.
  • A fourth student goes down the hall and changes every fourth locker.

This process continues up to the thousandth student! At the end of the process, which lockers will be open? (Hint: you may want to try this problem with a smaller number of lockers first.)

Summary

A factor of a whole number \(n\) is a whole number that divides \(n\) evenly without a remainder. For example, 1, 2, 3, 4, 6, and 12 are all factors of 12 because each of them divides 12 evenly and without a remainder.

A common factor of two whole numbers is a factor that they have in common. For example, 1, 3, 5, and 15 are factors of 45; they are also factors of 60. We call 1, 3, 5, and 15 common factors of 45 and 60.

The greatest common factor (sometimes written as GCF) of two whole numbers is the greatest of all of the common factors. For example, 15 is the greatest common factor for 45 and 60. 

One way to find the greatest common factor of two whole numbers is to list all of the factors for each, and then look for the greatest factor they have in common. Let’s try to find the greatest common factor of 18 and 24. First, we list all the factors of each number.

  • Factors of 18: 1, 2, 3, 6, 9,18

  • Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24

The common factors are 1, 2, 3, and 6. Of these, 6 is the greatest one, so 6 is the greatest common factor of 18 and 24.

Glossary Entries

  • common factor

    A common factor of two numbers is a number that divides evenly into both numbers. For example, 5 is a common factor of 15 and 20, because \(15 \div 5 = 3\) and \(20 \div 5 = 4\). Both of the quotients, 3 and 4, are whole numbers.

    • The factors of 15 are 1, 3, 5, and 15.
    • The factors of 20 are 1, 2, 4, 5, 10, and 20.
  • greatest common factor

    The greatest common factor of two numbers is the largest number that divides evenly into both numbers. Sometimes we call this the GCF. For example, 15 is the greatest common factor of 45 and 60.

    • The factors of 45 are 1, 3, 5, 9, 15, and 45.
    • The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.