Lesson 5
More Estimating Probabilities
Let’s estimate some probabilities.
5.1: Is it Likely?
- If the weather forecast calls for a 20% chance of light rain tomorrow, would you say that it is likely to rain tomorrow?
- If the probability of a tornado today is \(\frac{1}{10}\), would you say that there will likely be a tornado today?
- If the probability of snow this week is 0.85, would you say that it is likely to snow this week?
5.2: Making My Head Spin
Work with your group to decide which person will use each spinner. Make sure each person selects a different spinner.
Answer the first set of questions on your own.
Spinner A
Spinner B
Spinner C
Spinner D
- Spin your spinner 10 times and record your outcomes.
- Did you get all of the different possible outcomes in your 10 spins?
-
What fraction of your 10 spins landed on 3?
Work with your group to answer the next set of questions.
- Share your outcomes with your group and record their outcomes.
- Outcomes for spinner A:
- Outcomes for spinner B:
- Outcomes for spinner C:
- Outcomes for spinner D:
- Do any of the spinners have the same sample space? If so, do they have the same probabilities for each number to result?
- For each spinner, what is the probability that it ends on the number 3? Explain or show your reasoning.
- For each spinner, what is the probability that it lands on something other than the number 3? Explain or show your reasoning.
- Noah put spinner D on top of his closed binder and spun it 10 times. It never landed on the number 1. How might you explain why this happened?
- Han put spinner C on the floor and spun it 10 times. It never landed on the number 3, so he says that the probability of getting a 3 is 0. How might you explain why this happened?
Design a spinner that has a \(\frac{2}{3}\) probability of landing on the number 3. Explain how you could precisely draw this spinner.
5.3: How Much Green?
Your teacher will give you a bag of blocks that are different colors. Do not look into the bag or take out more than 1 block at a time. Repeat these steps until everyone in your group has had 4 turns.
- Take one block out of the bag and record whether or not it is green.
- Put the block back into the bag, and shake the bag to mix up the blocks.
- Pass the bag to the next person in the group.
- What do you think is the probability of taking out a green block from this bag? Explain or show your reasoning.
- How could you get a better estimate without opening the bag?
Summary
Suppose a bag contains 5 blocks. If we select a block at random from the bag, then the probability of getting any one of the blocks is \(\frac15\).
Now suppose a bag contains 5 blocks. Some of the blocks have a star, and some have a moon. If we select a block from the bag, then we will either get a star block or a moon block. The probability of getting a star block depends on how many there are in the bag.
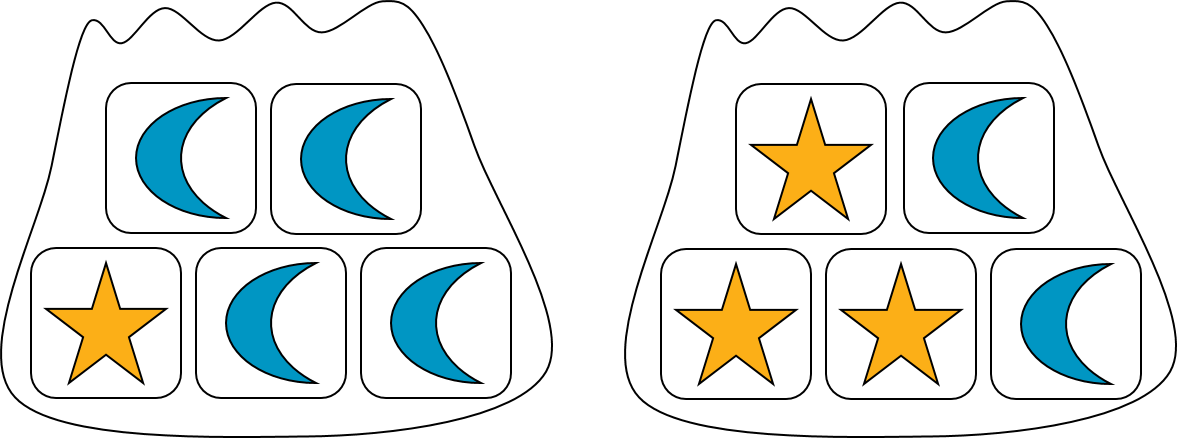
In this example, the probability of selecting a star block at random from the first bag is \(\frac15\), because it contains only 1 star block. (The probability of getting a moon block is \(\frac45\).) The probability of selecting a star block at random from the second bag is \(\frac35\), because it contains 3 star blocks. (The probability of getting a moon block from this bag is \(\frac25\).)
This shows that two experiments can have the same sample space, but different probabilities for each outcome.
Video Summary
Glossary Entries
- chance experiment
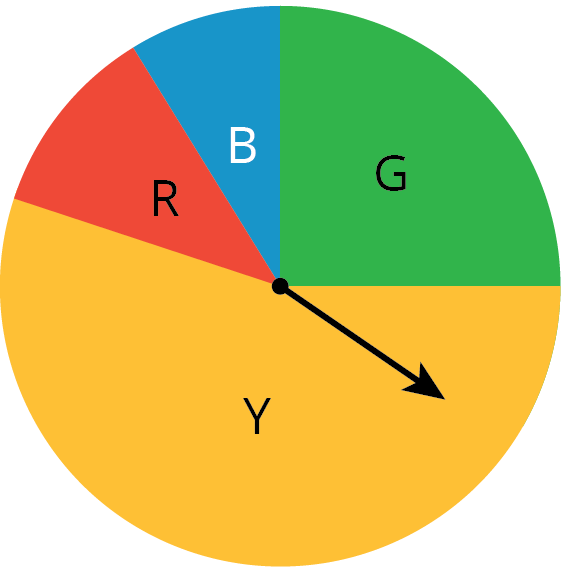
A chance experiment is something you can do over and over again, and you don’t know what will happen each time.
For example, each time you spin the spinner, it could land on red, yellow, blue, or green.
- event
An event is a set of one or more outcomes in a chance experiment. For example, if we roll a number cube, there are six possible outcomes.
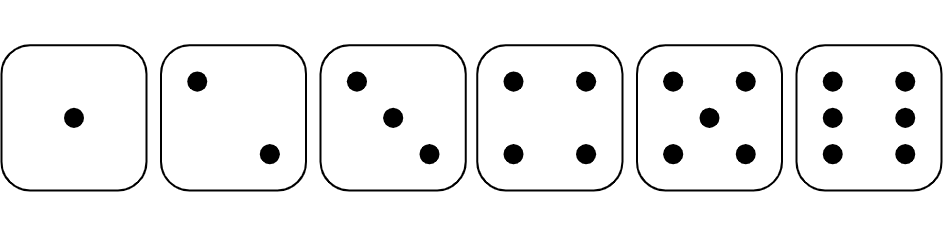
Examples of events are “rolling a number less than 3,” “rolling an even number,” or “rolling a 5.”
- outcome
An outcome of a chance experiment is one of the things that can happen when you do the experiment. For example, the possible outcomes of tossing a coin are heads and tails.
- probability
The probability of an event is a number that tells how likely it is to happen. A probability of 1 means the event will always happen. A probability of 0 means the event will never happen.
For example, the probability of selecting a moon block at random from this bag is \(\frac45\).

- random
Outcomes of a chance experiment are random if they are all equally likely to happen.
- sample space
The sample space is the list of every possible outcome for a chance experiment.
For example, the sample space for tossing two coins is:
heads-heads tails-heads heads-tails tails-tails