Lesson 16
Estimating Population Proportions
Let’s estimate population proportions using samples.
16.1: Getting to School
A teacher asked all the students in one class how many minutes it takes them to get to school. Here is a list of their responses:
- 20
- 10
- 15
- 8
- 5
- 15
- 10
- 5
- 20
- 5
- 15
- 10
- 3
- 10
- 18
- 5
- 25
- 5
- 5
- 12
- 10
- 30
- 5
- 10
-
What fraction of the students in this class say:
- it takes them 5 minutes to get to school?
- it takes them more than 10 minutes to get to school?
-
If the whole school has 720 students, can you use this data to estimate how many of them would say that it takes them more than 10 minutes to get to school?
Be prepared to explain your reasoning.
16.2: Reaction Times
The track coach at a high school needs a student whose reaction time is less than 0.4 seconds to help out at track meets. All the twelfth graders in the school measured their reaction times. Your teacher will give you a bag of papers that list their results.
- Work with your partner to select a random sample of 20 reaction times, and record them in the table.
- What proportion of your sample is less than 0.4 seconds?
- Estimate the proportion of all twelfth graders at this school who have a reaction time of less than 0.4 seconds. Explain your reasoning.
- There are 120 twelfth graders at this school. Estimate how many of them have a reaction time of less than 0.4 seconds.
-
Suppose another group in your class comes up with a different estimate than yours for the previous question.
-
What is another estimate that would be reasonable?
-
What is an estimate you would consider unreasonable?
-
16.3: A New Comic Book Hero
Here are the results of a survey of 20 people who read The Adventures of Super Sam regarding what special ability they think the new hero should have.

| response | what new ability? |
|---|---|
| 1 | fly |
| 2 | freeze |
| 3 | freeze |
| 4 | fly |
| 5 | fly |
| 6 | freeze |
| 7 | fly |
| 8 | super strength |
| 9 | freeze |
| 10 | fly |
| response | what new ability? |
|---|---|
| 11 | freeze |
| 12 | freeze |
| 13 | fly |
| 14 | invisibility |
| 15 | freeze |
| 16 | fly |
| 17 | freeze |
| 18 | fly |
| 19 | super strength |
| 20 | freeze |
- What proportion of this sample want the new hero to have the ability to fly?
-
If there are 2,024 dedicated readers of The Adventures of Super Sam, estimate the number of readers who want the new hero to fly.
Two other comic books did a similar survey of their readers.
- In a survey of people who read Beyond Human, 42 out of 60 people want a new hero to be able to fly.
- In a survey of people who read Mysterious Planets, 14 out of 40 people want a new hero to be able to fly.
- Do you think the proportion of all readers who want a new hero that can fly are nearly the same for the three different comic books? Explain your reasoning.
-
If you were in charge of these three comics, would you give the ability to fly to any of the new heroes? Explain your reasoning using the proportions you calculated.
16.4: Flying to the Shelves
The authors of The Adventures of Super Sam chose 50 different random samples of readers. Each sample was of size 20. They looked at the sample proportions who prefer the new hero to fly.
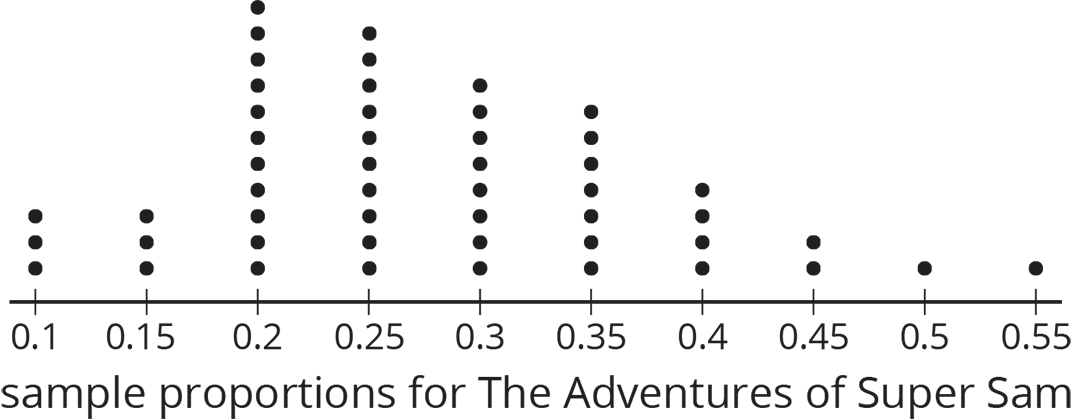
- What is a good estimate of the proportion of all readers who want the new hero to be able to fly?
- Are most of the sample proportions within 0.1 of your estimate for the population proportion?
-
If the authors of The Adventures of Super Sam give the new hero the ability to fly, will that please most of the readers? Explain your reasoning.
The authors of the other comic book series created similar dot plots.


-
For each of these series, estimate the proportion of all readers who want the new hero to fly.
- Beyond Human:
- Mysterious Planets:
- Should the authors of either of these series give their new hero the ability to fly?
- Why might it be more difficult for the authors of Mysterious Planets to make the decision than the authors of the other series?
Draw an example of a dot plot with at least 20 dots that represent the sample proportions for different random samples that would indicate that the population proportion is above 0.6, but there is a lot of uncertainty about that estimate.
Summary
Sometimes a data set consists of information that fits into specific categories. For example, we could survey students about whether they have a pet cat or dog. The categories for these data would be {neither, dog only, cat only, both}. Suppose we surveyed 10 students. Here is a table showing possible results:
| option | number of responses |
|---|---|
| neither dog nor cat | 2 |
| dog only | 4 |
| cat only | 1 |
| both dog and cat | 3 |
In this sample, 3 of the students said they have both a dog and a cat. We can say that the proportion of these students who have a both a dog and a cat is \(\frac{3}{10}\) or 0.3. If this sample is representative of all 720 students at the school, we can predict that about \(\frac{3}{10}\) of 720, or about 216 students at the school have both a dog and a cat.
In general, a proportion is a number from 0 to 1 that represents the fraction of the data that belongs to a given category.
Glossary Entries
- interquartile range (IQR)
The interquartile range is one way to measure how spread out a data set is. We sometimes call this the IQR. To find the interquartile range we subtract the first quartile from the third quartile.
For example, the IQR of this data set is 20 because \(50-30=20\).
22 29 30 31 32 43 44 45 50 50 59 Q1 Q2 Q3 - proportion
A proportion of a data set is the fraction of the data in a given category.
For example, a class has 20 students. There are 2 left-handed students and 18 right-handed students in the class. The proportion of students who are left-handed is \(\frac{2}{20}\), or 0.1.