Lesson 6
Scaling and Area
Lesson Narrative
This lesson is optional. In this lesson, students are introduced to how the area of a scaled copy relates to the area of the original shape. Students build on their grade 6 work with exponents to recognize that the area increases by the square of the scale factor by which the sides increased. Students will continue to work with the area of scaled shapes later in this unit and in later units in this course. Although the lesson is optional, it will be particularly helpful for students to have already had this introduction when they study the area of circles in a later unit.
In two of the activities in this lesson, students build scaled copies using pattern blocks as units of area. This work with manipulatives helps accustom students to a pattern that many find counterintuitive at first (MP8). (It is a common but false assumption that the area of scaled copies increases by the same scale factor as the sides.) After that, students calculate the area of scaled copies of parallelograms and triangles to apply the patterns they discovered in the hands-on activities (MP7).
Learning Goals
Teacher Facing
- Calculate and compare (orally and in writing) the areas of multiple scaled copies of the same shape.
- Generalize (orally) that the area of a scaled copy is the product of the area of the original figure and the “square” of the scale factor.
- Recognize that a two-dimensional attribute, like area, scales at a different rate than one-dimensional attributes, like length and distance.
Student Facing
Let's build scaled shapes and investigate their areas.
Required Materials
Required Preparation
Prepare to distribute the pattern blocks, at least 16 blue rhombuses, 16 green triangles, 10 red trapezoids, and 7 yellow hexagons per group of 3–4 students.
Copy and cut up the Area of Scaled Parallelograms and Triangles blackline master so each group of 2 students can get 1 of the 2 shapes.
Learning Targets
Student Facing
- I can describe how the area of a scaled copy is related to the area of the original figure and the scale factor that was used.
CCSS Standards
Glossary Entries
-
area
Area is the number of square units that cover a two-dimensional region, without any gaps or overlaps.
For example, the area of region A is 8 square units. The area of the shaded region of B is \(\frac12\) square unit.
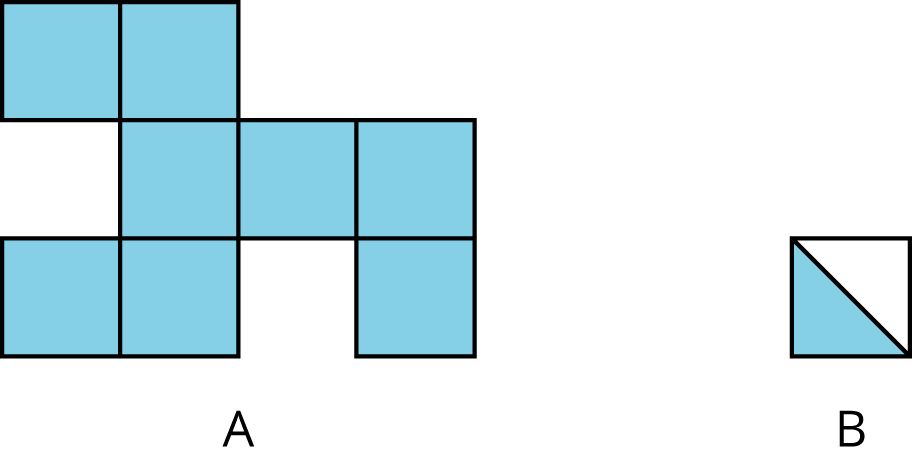
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |