Lesson 6
Scaling and Area
6.1: Scaling a Pattern Block (10 minutes)
Warm-up
By now, students understand that lengths in a scaled copy are related to the original lengths by the scale factor. Here they see that the area of a scaled copy is related to the original area by the square of the scale factor.
Students build scaled copies of a single pattern block, using blocks of the same shape to do so. They determine how many blocks are needed to create a copy at each specified scale factor. Each pattern block serves as an informal unit of area. Because each original shape has an area of 1 block, the \(\text{(scale factor)}^2\) pattern for the area of a scaled copy is easier to recognize.
Students use the same set of scale factors to build copies of three different shapes (a rhombus, a triangle, and a hexagon). They notice regularity in their repeated reasoning and use their observations to predict the number of blocks needed to build other scaled copies (MP8).
Launch
Arrange students in groups of 3–4. Distribute pattern blocks and ask students to use them to build scaled copies of each shape as described in the task. Each group would need at most 16 blocks each of the green triangle, the blue rhombus, and the red trapezoid. If there are not enough for each group to have a full set with 16 each of the green, blue, and red blocks, consider rotating the blocks of each color through the groups, or having students start with 10 blocks of each and ask for more as needed.
Give students 6–7 minutes to collaborate on the task and follow with a whole-class discussion. Make sure all students understand that “twice as long” means “2 times as long.”
Using real pattern blocks is preferred, but the Digital Activity can replace the manipulatives if they are unavailable.
Student Facing
Use the applets to explore the pattern blocks. Work with your group to build the scaled copies described in each question.

- How many blue rhombus blocks does it take to build a scaled copy of Figure A:
-
Where each side is twice as long?
-
Where each side is 3 times as long?
-
Where each side is 4 times as long?
-
- How many green triangle blocks does it take to build a scaled copy of Figure B:
-
Where each side is twice as long?
-
Where each side is 3 times as long?
-
Using a scale factor of 4?
-
- How many red trapezoid blocks does it take to build a scaled copy of Figure C:
-
Using a scale factor of 2?
-
Using a scale factor of 3?
-
Using a scale factor of 4?
-
- Make a prediction: How many blocks would it take to build scaled copies of these shapes using a scale factor of 5? Using a scale factor of 6? Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 3–4. Distribute pattern blocks and ask students to use them to build scaled copies of each shape as described in the task. Each group would need at most 16 blocks each of the green triangle, the blue rhombus, and the red trapezoid. If there are not enough for each group to have a full set with 16 each of the green, blue, and red blocks, consider rotating the blocks of each color through the groups, or having students start with 10 blocks of each and ask for more as needed.
Give students 6–7 minutes to collaborate on the task and follow with a whole-class discussion. Make sure all students understand that “twice as long” means “2 times as long.”
Using real pattern blocks is preferred, but the Digital Activity can replace the manipulatives if they are unavailable.
Student Facing
Your teacher will give you some pattern blocks. Work with your group to build the scaled copies described in each question.

-
How many blue rhombus blocks does it take to build a scaled copy of Figure A:
-
Where each side is twice as long?
-
Where each side is 3 times as long?
-
Where each side is 4 times as long?
-
-
How many green triangle blocks does it take to build a scaled copy of Figure B:
-
Where each side is twice as long?
-
Where each side is 3 times as long?
-
Using a scale factor of 4?
-
-
How many red trapezoid blocks does it take to build a scaled copy of Figure C:
-
Using a scale factor of 2?
-
Using a scale factor of 3?
-
Using a scale factor of 4?
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may come up with one of these arrangements for the first question, because they assume the answer will take 2 blocks to build:

You could use one pattern block to demonstrate measuring the lengths of the sides of their shape, to show them which side they have not doubled.
Students may also come up with:

for tripling the trapezoid, because they triple the height of the scaled copy but they do not triple the length. You could use the process described above to show that not all side lengths have tripled.
Activity Synthesis
Display a table with only the column headings filled in. For the first four rows, ask different students to share how many blocks it took them to build each shape and record their answers in the table.
| scale factor | number of blocks to build Figure A | number of blocks to build Figure B | number of blocks to build Figure C |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 10 | |||
| \(s\) | |||
| \(\frac{1}{2}\) |
To help student notice, extend, and generalize the pattern in the table, guide a discussion using questions such as these:
- In the table, how is the number of blocks related to the scale factor? Is there a pattern?
- How many blocks are needed to build scaled copies using scale factors of 5 or 10? How do you know?
- How many blocks are needed to build a scaled copy using any scale factor \(s\)?
- If we want a scaled copy where each side is half as long, how much of a block would it take? How do you know? Does the same rule still apply?
If not brought up by students, highlight the fact that the number of blocks it took to build each scaled shape equals the scale factor times itself, regardless of the shape (look at the table row for \(s\)). This rule applies to any factor, including those that are less than 1.
6.2: Scaling More Pattern Blocks (10 minutes)
Optional activity
This activity extends the conceptual work of the previous one by adding a layer of complexity. Here, the original shapes are comprised of more than 1 block, so the number of blocks needed to build their scaled copies is not simply \(\text{(scale factor)}^2\), but rather \(n \times \text{(scale factor)}^2\), where \(n\) is the number of blocks in the original shape. Students begin to think about how the scaled area relates to the original area, which is no longer 1 area unit. They notice that the pattern \(\text{(scale factor)}^2\) presents itself in the factor by which the original number of blocks has changed, rather than in the total number of blocks in the copy.
As in the previous task, students observe regularity in repeated reasoning (MP8), noticing that regardless of the shapes, starting with \(n\) pattern blocks and scaling by \(s\) uses \(ns^2\) pattern blocks.
Also as in the previous task, the shape composed of trapezoids might be more challenging to scale than those composed of rhombuses and triangles. Prepare to support students scaling the red shape by offering some direction or additional time, if feasible.
As students work, monitor for groups who notice that the pattern of squared scale factors still occurs here, and that it is apparent if the original number of blocks is taken into account. Select them to share during class discussion.
Launch
Keep students in the same groups, or form combined groups if there are not enough blocks. Assign one shape for each group to build (or let groups choose a shape, as long as all 3 shapes are equally represented). To build a copy of each given shape using a scale factor of 2, groups will need 12 blue rhombuses, 8 red trapezoids, or 16 green triangles. To completely build a copy of each given shape with a scale factor of 3, they would need 27 blue rhombuses, 18 red trapezoids, and 36 green triangles; however, the task prompts them to stop building when they know what the answer will be.
Give students 6–7 minutes to build their shapes and complete the task. Remind them to use the same blocks as those in the original shape and to check the side lengths of each built shape to make sure they are properly scaled.
Using real pattern blocks is preferred, but the Digital Activity can replace the manipulatives if they are unavailable.
Supports accessibility for: Organization; Attention
Student Facing
Your teacher will assign your group one of these figures, each made with original-size blocks.
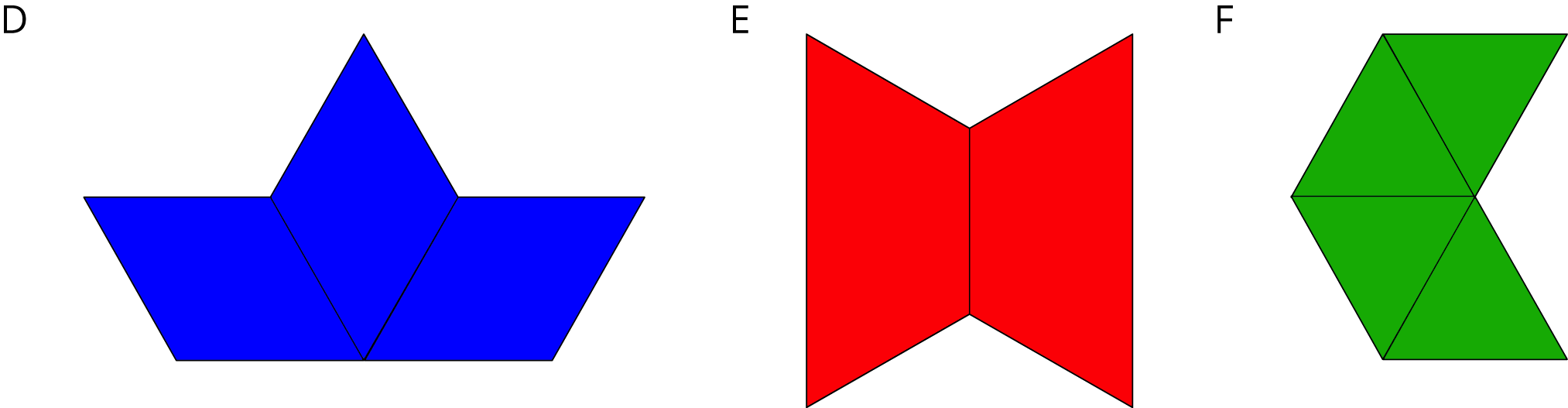
-
In the applet, move the slider to see a scaled copy of your assigned shape, using a scale factor of 2. Use the original-size blocks to build a figure to match it. How many blocks did it take?
-
Your classmate thinks that the scaled copies in the previous problem will each take 4 blocks to build. Do you agree or disagree? Explain you reasoning.
-
Move the slider to see a scaled copy of your assigned shape using a scale factor of 3. Start building a figure with the original-size blocks to match it. Stop when you can tell for sure how many blocks it would take. Record your answer.
-
Predict: How many blocks would it take to build scaled copies using scale factors 4, 5, and 6? Explain or show your reasoning.
-
How is the pattern in this activity the same as the pattern you saw in the previous activity? How is it different?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Keep students in the same groups, or form combined groups if there are not enough blocks. Assign one shape for each group to build (or let groups choose a shape, as long as all 3 shapes are equally represented). To build a copy of each given shape using a scale factor of 2, groups will need 12 blue rhombuses, 8 red trapezoids, or 16 green triangles. To completely build a copy of each given shape with a scale factor of 3, they would need 27 blue rhombuses, 18 red trapezoids, and 36 green triangles; however, the task prompts them to stop building when they know what the answer will be.
Give students 6–7 minutes to build their shapes and complete the task. Remind them to use the same blocks as those in the original shape and to check the side lengths of each built shape to make sure they are properly scaled.
Using real pattern blocks is preferred, but the Digital Activity can replace the manipulatives if they are unavailable.
Supports accessibility for: Organization; Attention
Student Facing
Your teacher will assign your group one of these figures.

-
Build a scaled copy of your assigned shape using a scale factor of 2. Use the same shape blocks as in the original figure. How many blocks did it take?
-
Your classmate thinks that the scaled copies in the previous problem will each take 4 blocks to build. Do you agree or disagree? Explain you reasoning.
-
Start building a scaled copy of your assigned figure using a scale factor of 3. Stop when you can tell for sure how many blocks it would take. Record your answer.
-
How many blocks would it take to build scaled copies of your figure using scale factors 4, 5, and 6? Explain or show your reasoning.
-
How is the pattern in this activity the same as the pattern you saw in the previous activity? How is it different?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
-
How many blocks do you think it would take to build a scaled copy of one yellow hexagon where each side is twice as long? Three times as long?
-
Figure out a way to build these scaled copies.
-
Do you see a pattern for the number of blocks used to build these scaled copies? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may forget to check that the lengths of all sides of their shape have been scaled and end with an inaccurate count of the pattern blocks. Remind them that all segments must be scaled by the same factor.
Activity Synthesis
The goal of this discussion is to ensure that students understand that the pattern for the number of blocks in the scaled copies depends both on the scale factor and on the number of blocks in the pattern.
Display a table with only the column headings filled in. Poll the class on how many blocks it took them to build each scaled copy using the factors of 2 and 3. Record their answers in the table.
| scale factor | number of blocks to build Figure D | number of blocks to build Figure E | number of blocks to build Figure F |
|---|---|---|---|
| 1 | 3 | 2 | 4 |
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| \(s\) |
Consider displaying the built shapes or pictures of them for all to see.



Invite selected students to share the pattern that their groups noticed and used to predict the number of blocks needed for copies with scale factors 4, 5, and 6. Record their predictions in the table. Discuss:
- How does the pattern for the number of blocks in this activity compare to the pattern in the previous activity? Are they related? How?
- For each figure, how many blocks does it take to build a copy using any scale factor \(s\)?
Design Principle(s): Optimize output (for explanation)
6.3: Area of Scaled Parallelograms and Triangles (15 minutes)
Optional activity
In this activity, students transfer what they learned with the pattern blocks to calculate the area of other scaled shapes (MP8). In groups of 2, students draw scaled copies of either a parallelogram or a triangle and calculate the areas. Then, each group compares their results with those of a group that worked on the other shape. They find that the scaled areas of two shapes are the same (even though the starting shapes are different and have different measurements) and attribute this to the fact that the two shapes had the same original area and were scaled using the same scale factors.

While students are not asked to reason about scaled areas by tiling (as they had done in the previous activities), each scaled copy can be tiled to illustrate how length measurements have scaled and how the original area has changed. Some students may choose to draw scaled copies and think about scaled areas this way.

As students find the areas of copies with scale factors 5 and \(\frac35\) without drawing (for the last question), monitor for these methods, depending on their understanding of or comfort with the \(\text{(scale factor)}^2\) pattern:
- Scaling the original base and height and then multiplying to find the area
- Multiplying the original area by the square of the scale factor
Select students using each approach. Invite them to share their reasoning, sequenced in this order, during the discussion.
You will need the Area of Scaled Parallelograms and Triangles blackline master for this activity.
Launch
Arrange students in groups of 2. Provide access to geometry toolkits.
Distribute slips showing the parallelogram to half the groups and the triangle to the others. Give students 1 minute of quiet work time for the first question, and then time to complete the rest of the task with their partner.
Supports accessibility for: Social-emotional skills; Conceptual processing
Student Facing
- Your teacher will give you a figure with measurements in centimeters. What is the area of your figure? How do you know?
- Work with your partner to draw scaled copies of your figure, using each scale factor in the table. Complete the table with the measurements of your scaled copies.
scale factor base (cm) height (cm) area (cm2) 1 2 3 \(\frac{1}{2}\) \(\frac{1}{3}\) - Compare your results with a group that worked with a different figure. What is the same about your answers? What is different?
- If you drew scaled copies of your figure with the following scale factors, what would their areas be? Discuss your thinking. If you disagree, work to reach an agreement. Be prepared to explain your reasoning.
scale factor area (cm2) 5 \(\frac{3}{5}\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not remember how to calculate the area of parallelograms and triangles. Make sure that they have the correct area of 10 square units for their original shape before they calculate the area of their scaled copies.
When drawing their scaled copies, some students might not focus on making corresponding angles equal. As long as they scale the base and height of their polygon correctly, this will not impact their area calculations. If time permits, however, prompt them to check their angles using tracing paper or a protractor.
Some students might focus unnecessarily on measuring other side lengths of their polygon, instead of attending only to base and height. If time is limited, encourage them to scale the base and height carefully and check or measure the angles instead.
Activity Synthesis
Invite selected students to share their solutions. Then focus class discussion on two themes: how the values in the tables for the two shapes compare, and how students determined the scaled areas for the scale factors 5 and \(\frac35\). Ask questions such as:
- What did you notice when you compared your answerswithanother group that worked with the other figure? (When the scale factors are the same, the scaled areas are the same, though the bases and heights are different.)
- How did you find the scaled areas for scale factors of 5 and \(\frac35\)? (By scaling the original base and height and multiplying the scaled measurements; by multiplying the original area by \(\text{(scale factor)}^2\).)
- How is the process for finding scaled area here the same as and different than that in the previous activities with pattern blocks? (The area units are different; the pattern of squaring the scale factor is the same.)
Highlight the connection between the two ways of finding scaled areas. Point out that when we multiply the base and height each by the scale factor and then multiply the results, we are essentially multiplying the original lengths by the scale factor two times. The effect of this process is the same as multiplying the original area by \(\text{(scale factor)}^2\).
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
- If all the dimensions of a scaled copy are twice as long as in the original shape, will the area of the scaled copy be twice as large? (No)
- Why not? (Both the length and the width get multiplied by 2, so the area gets multiplied by 4.)
- If the scale factor is 5, how many times larger will the scaled copy’s area be? (25 times larger)
6.4: Cool-down - Enlarged Areas (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Scaling affects lengths and areas differently. When we make a scaled copy, all original lengths are multiplied by the scale factor. If we make a copy of a rectangle with side lengths 2 units and 4 units using a scale factor of 3, the side lengths of the copy will be 6 units and 12 units, because \(2\boldcdot 3 = 6\) and \(4\boldcdot 3 = 12\).
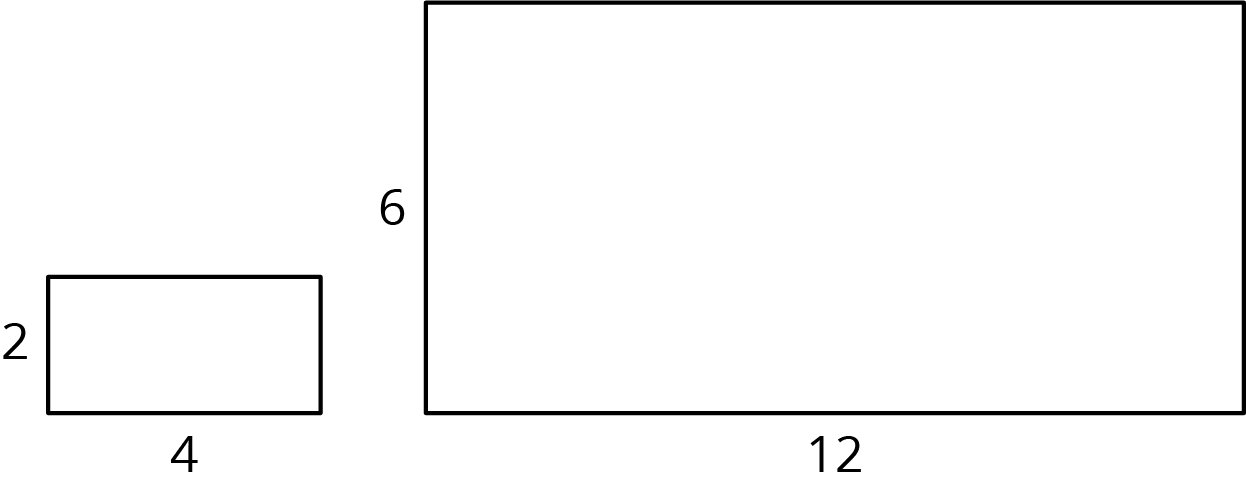
The area of the copy, however, changes by a factor of (scale factor)2. If each side length of the copy is 3 times longer than the original side length, then the area of the copy will be 9 times the area of the original, because \(3\boldcdot 3\), or \(3^2\), equals 9.
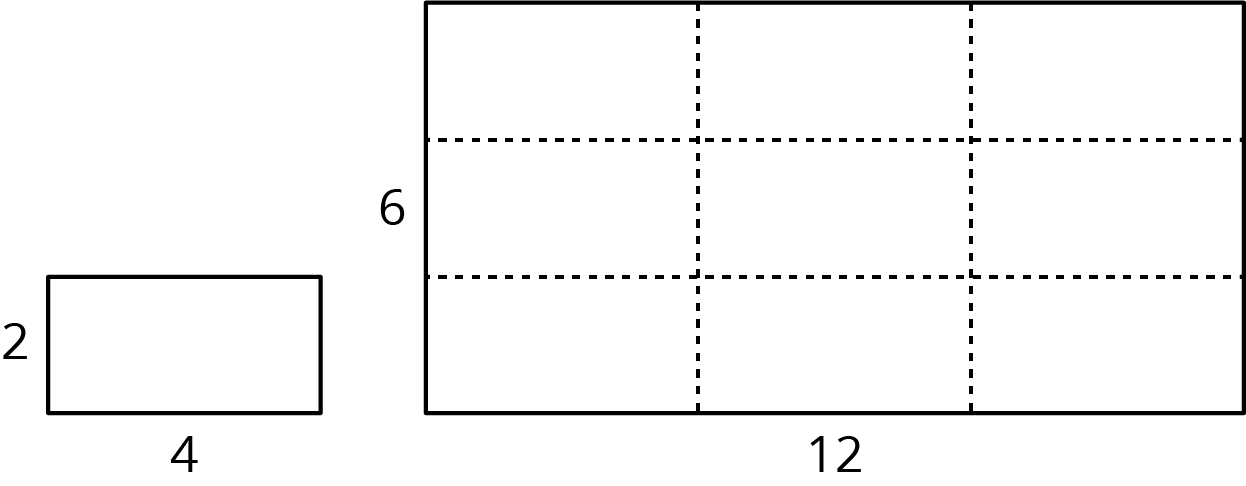
In this example, the area of the original rectangle is 8 units2 and the area of the scaled copy is 72 units2, because \(9\boldcdot 8 = 72\). We can see that the large rectangle is covered by 9 copies of the small rectangle, without gaps or overlaps. We can also verify this by multiplying the side lengths of the large rectangle: \(6\boldcdot 12=72\).
Lengths are one-dimensional, so in a scaled copy, they change by the scale factor. Area is two-dimensional, so it changes by the square of the scale factor. We can see this is true for a rectangle with length \(l\) and width \(w\). If we scale the rectangle by a scale factor of \(s\), we get a rectangle with length \(s\boldcdot l\) and width \(s\boldcdot w\). The area of the scaled rectangle is \(A = (s\boldcdot l) \boldcdot (s\boldcdot w)\), so \(A= (s^2) \boldcdot (l \boldcdot w)\). The fact that the area is multiplied by the square of the scale factor is true for scaled copies of other two-dimensional figures too, not just for rectangles.