Lesson 5
The Size of the Scale Factor
5.1: Number Talk: Missing Factor (10 minutes)
Warm-up
This number talk encourages students to use structure and the relationship between multiplication and division to mentally solve problems involving fractions. It prompts students to think about how the size of factors impacts the size of the product. It reviews the idea of reciprocal factors in preparation for the work in the lesson.
Launch
Ask students what operation is meant when a number and a variable are placed right next to each other in an equation. (Multiplication)
Display one problem at a time. Give students 1 minute of quiet think time per problem and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Solve each equation mentally.
\(16x=176\)
\(16x=8\)
\(16x=1\)
\(\frac15x=1\)
\(\frac25x=1\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might think that a product cannot be less than one of the factors, not realizing that one of the factors can be a fraction. Use examples involving smaller and familiar numbers to remind them that it is possible. Ask, for example, “What times 10 is 5?”
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see. To involve more students in the conversation, consider asking:
- Who can restate ___’s reasoning in a different way?
- Did anyone solve the problem the same way but would explain it differently?
- Did anyone solve the problem in a different way?
- Does anyone want to add on to _____’s strategy?
- Do you agree or disagree? Why?
Highlight that multiplying a factor by a fraction less than 1 results in a product that is less than one of the factors, and that two factors that multiply to be 1 are reciprocals.
Design Principle(s): Optimize output (for explanation)
5.2: Card Sort: Scaled Copies (15 minutes)
Activity
Students have studied many examples of scaled copies and know that corresponding lengths in a figure and its scaled copy are related by the same scale factor. The purpose of this activity is for students to examine how the size of the scale factor is related to the original figure and the scaled copy. The activity serves several purposes:
- To reinforce students’ awareness of scale factors
- To draw attention to how scaled copies behave when the scale factor is 1, less than 1, and greater than 1; and
- To help students notice that reciprocal scale factors reverse the scaling.
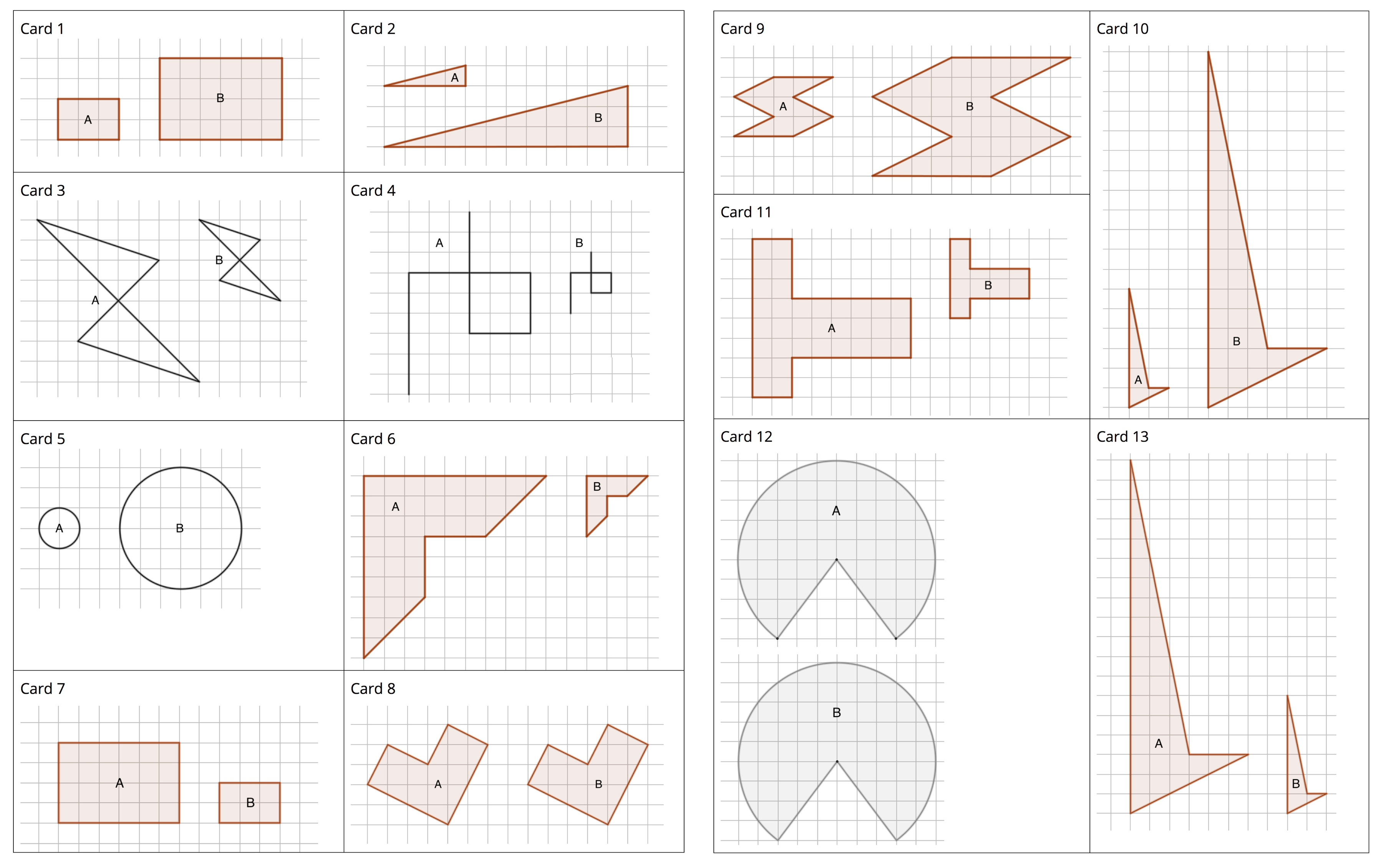
Monitor for students who group the cards in terms of:
- Specific scale factors (e.g., 2, 3, \(\frac12\), etc.)
- Ranges of scale factors producing certain effects (e.g., factors producing larger, unchanged, or smaller copies)
- Reciprocal scale factors (e.g., one factor scales Figure A to B, and its reciprocal reverses the scaling)
Select groups who use each of these approaches (and any others) and ask them to share during the discussion.
Launch
Arrange students in groups of 3–4. Distribute one set of slips to each group. Give students 7–8 minutes of group work time, followed by whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Your teacher will give you a set of cards. On each card, Figure A is the original and Figure B is a scaled copy.
-
Sort the cards based on their scale factors. Be prepared to explain your reasoning.
-
Examine cards 10 and 13 more closely. What do you notice about the shapes and sizes of the figures? What do you notice about the scale factors?
-
Examine cards 8 and 12 more closely. What do you notice about the figures? What do you notice about the scale factors?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Triangle B is a scaled copy of Triangle A with scale factor \(\frac12\).
- How many times bigger are the side lengths of Triangle B when compared with Triangle A?
- Imagine you scale Triangle B by a scale factor of \(\frac12\) to get Triangle C. How many times bigger will the side lengths of Triangle C be when compared with Triangle A?
- Triangle B has been scaled once. Triangle C has been scaled twice. Imagine you scale triangle A \(n\) times to get Triangle N, always using a scale factor of \(\frac12\). How many times bigger will the side lengths of Triangle N be when compared with Triangle A?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may sort by the types of figures rather than by how the second figure in each pair is scaled from the first. Remind students to sort based on how Figure A is scaled to create Figure B.
Students may think of the change in lengths between Figures A and B in terms of addition or subtraction, rather than multiplication or division. Remind students of an earlier lesson in which they explored the effect of subtracting the same length from each side of a polygon in order to scale it. What happened to the copy? (It did not end up being a polygon and was not a scaled copy of the original one.)
Students may be unclear as to how to describe how much larger or smaller a figure is, or may not recall the meaning of scale factor. Have them compare the lengths of each side of the figure. What is the common factor by which each side is multiplied?
Activity Synthesis
Select groups to explain their sorting decisions following the sequence listed in the Activity Narrative. If no groups sorted in terms of ranges of scale factors (less than 1, exactly 1, and greater than 1) or reciprocal scaling, ask:
- What can we say about the scale factors that produce larger copies? Smaller copies? Same-size copies?
- Some cards had the same pair of figures on them, just in a reversed order (i.e., pairs #1 and 7, #10 and 13). What do you notice about their scale factors?
Highlight the two main ideas of the lesson: 1) the effects of scale factors that are greater than 1, exactly 1, and less than 1; and 2) the reversibility of scaling. Point out that if Figure B is a scaled copy of Figure A, then A is also a scaled copy of B. In other words, A and B are scaled copies of one another, and their scale factors are reciprocals.
Suggest students add these observations to their answer for the last question.
Design Principle(s): Maximize meta-awareness
5.3: Scaling A Puzzle (15 minutes)
Optional activity
This activity gives students a chance to apply what they know about scale factors, lengths, and angles and create scaled copies without the support of a grid. Students work in groups of 3 to complete a jigsaw puzzle, each group member scaling 2 non-adjacent pieces of a 6-piece puzzle with a scale factor of \(\frac12\). The group then assembles the scaled pieces and examines the accuracy of their scaled puzzle. Consider having students use a color in place of the cross hatching.
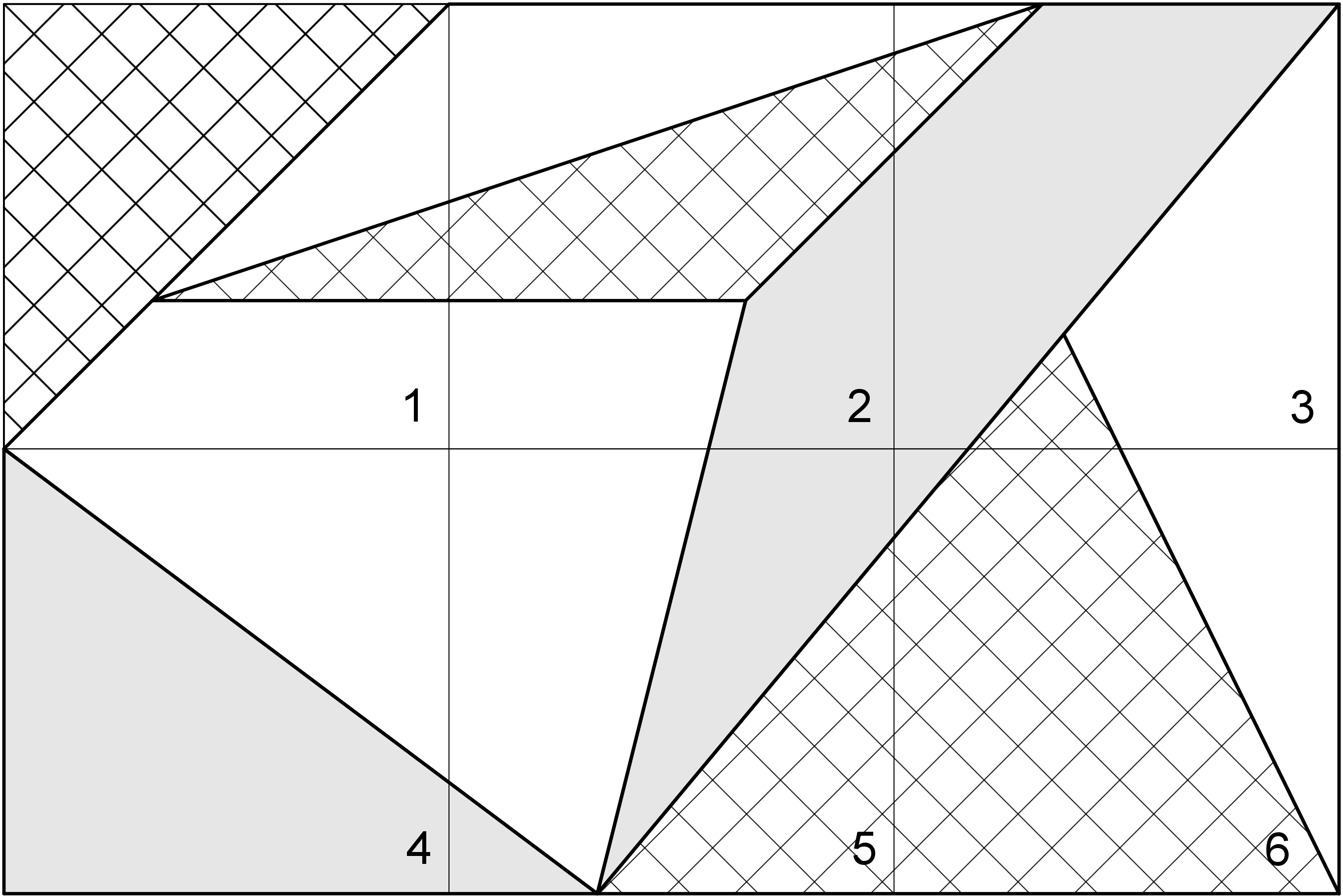

As students work, notice how they measure distances and whether they consider angles. Depending on how students determine scaled distances, they may not need to transfer angles. Look out for students who measure only the lengths of drawn segments rather than distances, e.g., between the corner of a square and where a segment begins. Suggest that they consider other measurements that might help them locate the beginning and end of a segment.
You will need the Scaling a Puzzle blackline master for this activity.
Launch
Arrange students in groups of 3. Give pre-cut puzzle squares 1 and 5 to one student in the group, squares 2 and 6 to a second student, and squares 3 and 4 to the third. After students have answered the first question, give each student 2 blank squares cut from the second section of the blackline master, whose sides are half of the side length of the puzzle squares. Provide access to geometry toolkits.
Supports accessibility for: Visual-spatial processing; Conceptual processing; Fine-motor skills
Student Facing
Your teacher will give you 2 pieces of a 6-piece puzzle.
- If you drew scaled copies of your puzzle pieces using a scale factor of \(\frac12\), would they be larger or smaller than the original pieces? How do you know?
- Create a scaled copy of each puzzle piece on a blank square, with a scale factor of \(\frac12\).
- When everyone in your group is finished, put all 6 of the original puzzle pieces together like this:
- Revise any of the scaled copies that may have been drawn incorrectly.
- If you were to lose one of the pieces of the original puzzle, but still had the scaled copy, how could you recreate the lost piece?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may incorporate the scale factor when scaling line segments but neglect to do so when scaling distances between two points not connected by a segment. Remind them that all distances are scaled by the same factor.
Students may not remember to verify that the angles in their copies must remain the same as the original. Ask them to notice the angles and recall what happens to angles when a figure is a scaled copy.
Activity Synthesis
Much of the conversations about creating accurate scaled copies will have taken place among partners, but consider coming together as a class to reflect on the different ways students worked. Ask questions such as:
- How is this task more challenging than creating scaled copies of polygons on a grid?
- Besides distances or lengths, what helped you create an accurate copy?
- How did you know or decide which distances to measure?
- Before your drawings were assembled, how did you check if they were correct?
Student responses to these questions may differ: for example, for piece 6, the two lines can be drawn by measuring distances on the border of the puzzle piece; the angles work out correctly automatically. For piece 2, however, to get the three lines that meet in a point in the middle of the piece just right, students can either measure angles, or extend those line segments until they meet the border of the piece (and then measure distances).
5.4: Missing Figure, Factor, or Copy (10 minutes)
Optional activity
In this activity, students investigate different aspects of the figure, scaled copy, and scale factor trio. Given any two of these three, we can find the third. Students work with these different scenarios on a grid, dealing with scale factors greater than 1, less than 1, and equal to 1. In addition, they create a scaled copy of a non-polygonal figure off of a grid.
Both on and off of a grid, students need to decide what tools to use (MP5) in order to measure angles and side lengths in order to produce the scaled copies.
Launch
Arrange students in groups of 2. Provide access to geometry toolkits. Give students 3–4 minutes of quiet work time, followed by 2 minutes of group discussion and then whole-class discussion.
Student Facing
-
What is the scale factor from the original triangle to its copy? Explain or show your reasoning.
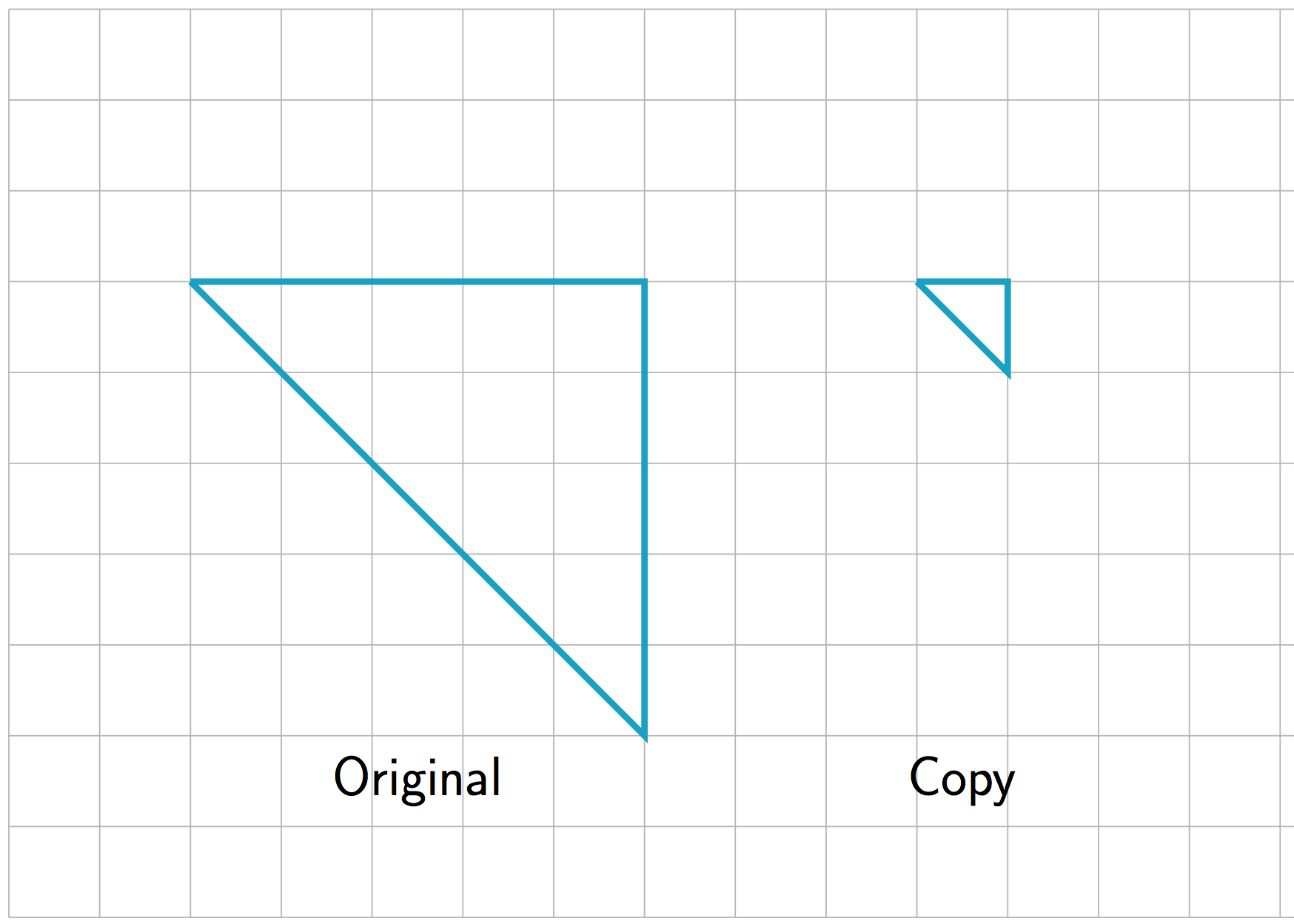
-
The scale factor from the original trapezoid to its copy is 2. Draw the scaled copy.
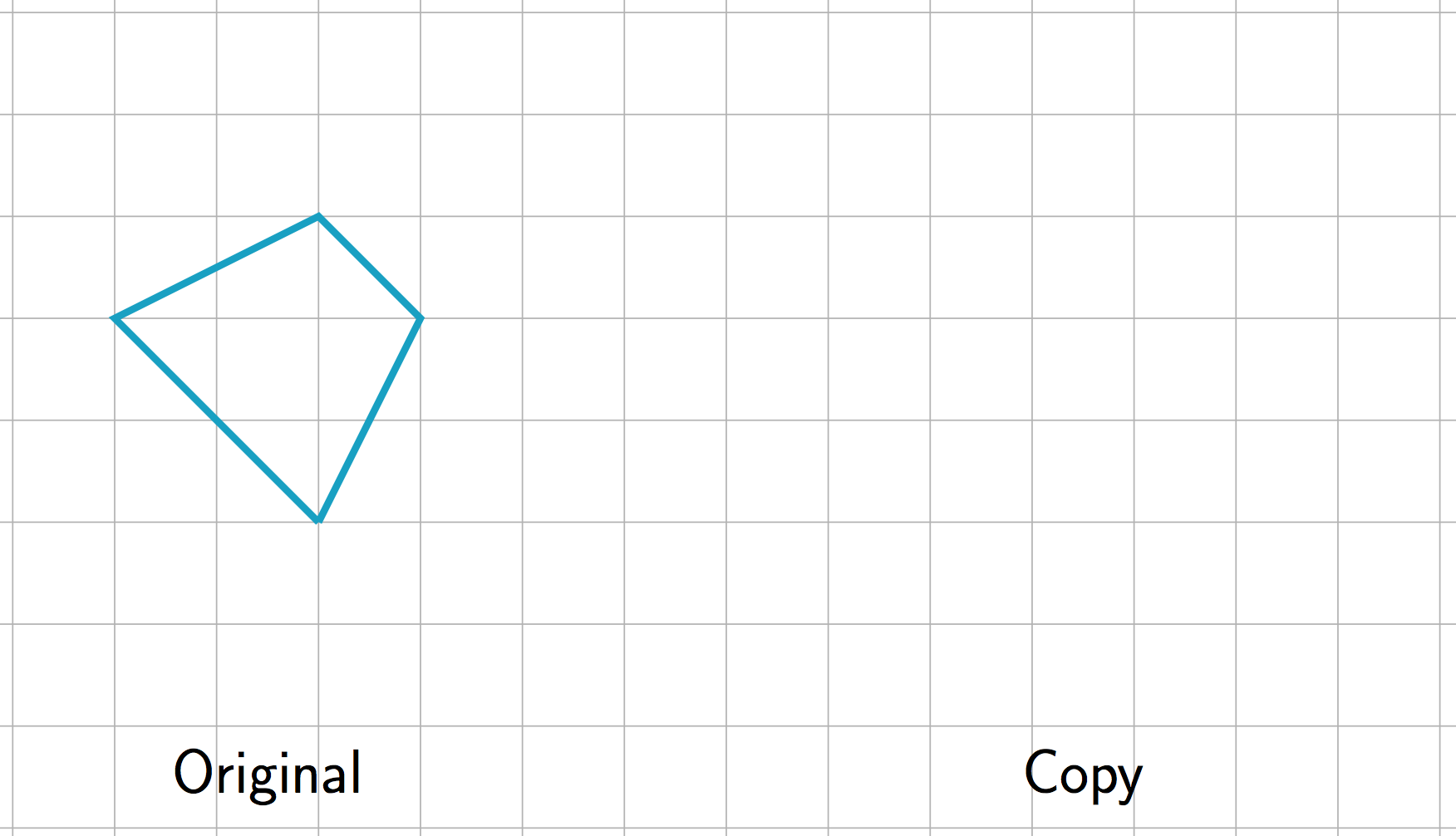
- The scale factor from the original figure to its copy is \(\frac32\). Draw the original figure.
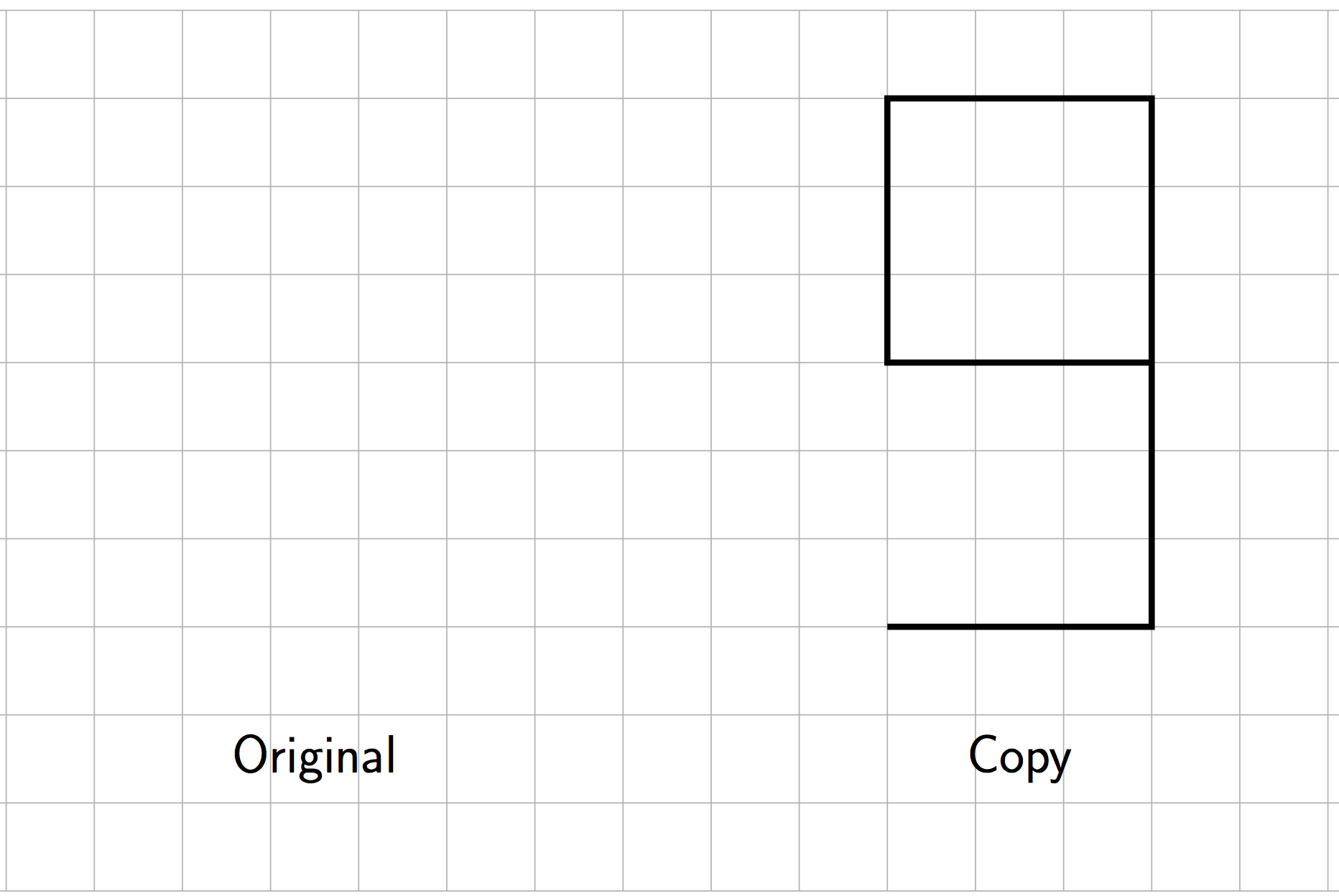
- What is the scale factor from the original figure to the copy? Explain how you know.

- The scale factor from the original figure to its scaled copy is 3. Draw the scaled copy.

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is to ensure that students understand the connections between the original figure, scaled copy, and scale
factor—given any two of the the three, they should understand a method for finding the third.
Ask students how they solved the first three questions. Which one was most challenging? Why? Individual responses will likely vary here, but the question with the missing original figure deserves special attention. This requires going backward since we have the scaled copy and the scale factor. This scenario also reinforces that the way to “undo” the scale factor of \(\frac{3}{2}\) that has been applied to produce the copy is to apply a scale factor
of \(\frac{2}{3}\).
For the last problem, ask students how they used the segment lengths and angles of the original figure. They may have sketched the copy without checking angles. Ask them why measuring angles is important.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
- What happens to the copy when it is created with a scale factor greater than 1? Less than 1? Exactly 1?
- How can we reverse the scaling to get back to the original figure when we have a scaled copy?
When the scale factor is greater than 1, the scaled copy is larger than the original. When it is less than 1, the copy is smaller than the original. A scale factor of exactly 1 produces a same-size copy.
Scaling can be reversed by using reciprocal factors. If we scale Figure A by a factor of 4 to obtain Figure B, we can scale B back to A using a factor of \(\frac14\). This means that if B is a scaled copy of A, A is also a scaled copy of B; they are scaled copies of each other.
5.5: Cool-down - Scaling a Rectangle (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The size of the scale factor affects the size of the copy. When a figure is scaled by a scale factor greater than 1, the copy is larger than the original. When the scale factor is less than 1, the copy is smaller. When the scale factor is exactly 1, the copy is the same size as the original.
Triangle \(DEF\) is a larger scaled copy of triangle \(ABC\), because the scale factor from \(ABC\) to \(DEF\) is \(\frac32\). Triangle \(ABC\) is a smaller scaled copy of triangle \(DEF\), because the scale factor from \(DEF\) to \(ABC\) is \(\frac23\).
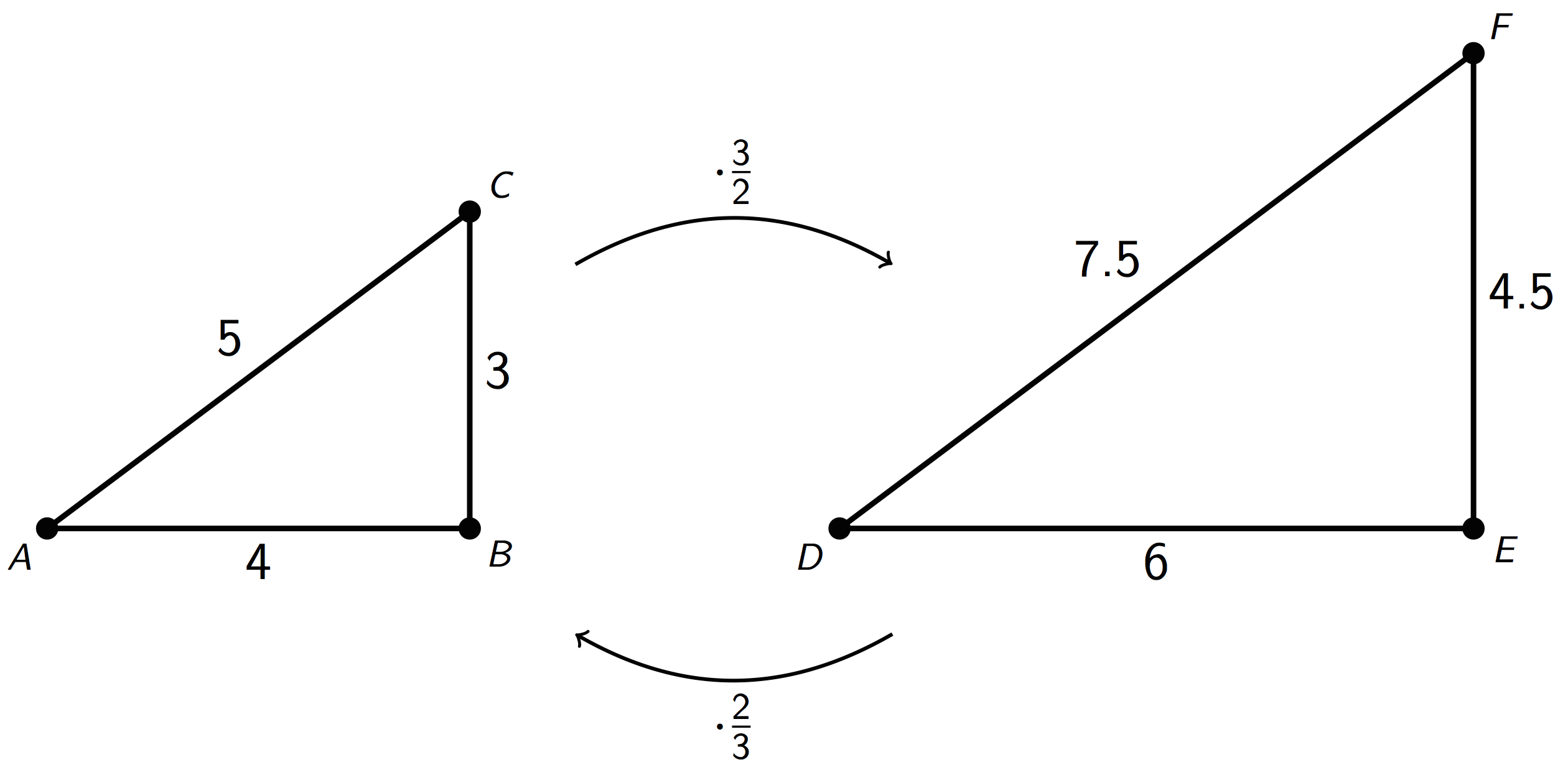
This means that triangles \(ABC\) and \(DEF\) are scaled copies of each other. It also shows that scaling can be reversed using reciprocal scale factors, such as \(\frac23\) and \(\frac32\).
In other words, if we scale Figure A using a scale factor of 4 to create Figure B, we can scale Figure B using the reciprocal scale factor, \(\frac14\), to create Figure A.