Lesson 2
Corresponding Parts and Scale Factors
2.1: Number Talk: Multiplying by a Unit Fraction (5 minutes)
Warm-up
This number talk allows students to review multiplication strategies, refreshing the idea that multiplying by a unit fraction is the same as dividing by its whole number reciprocal. It encourages students to use the structure of base ten numbers and the properties of operations to find the product of two whole numbers (MP7). For example, a student might find \(72 \boldcdot \frac{1}{9}\) (or \(72 \div 9\)) and then shift the decimal one place to the right in order to evaluate \((7.2) \boldcdot \frac{1}{9}\). Each problem was chosen to elicit different approaches, so as students share theirs, ask how the factors in each problem impacted their strategies.
Before students begin, consider establishing a small, discreet hand signal (such as a thumbs-up) students can display to indicate they have an answer that they can support by reasoning. Discreet signaling is a quick way for teachers to gather feedback about timing. It also keeps students from being distracted or rushed by raised hands around the class.
Launch
Display one problem at a time. Give students up to 1 minute of quiet think time per problem and ask them to give a signal when they have an answer and a strategy. Follow with a brief whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find each product mentally.
\(\frac14 \boldcdot 32\)
\((7.2) \boldcdot \frac19\)
\(\frac14 \boldcdot (5.6)\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see. If students express strategies in terms of division, ask if that strategy would work for any multiplication problem involving fractions. Highlight that these problems only involve unit fractions and division by the denominator is a strategy that works when multiplying by a unit fraction.
To involve more students in the conversation, consider asking:
- Who can restate ___’s reasoning in a different way?
- Did anyone solve the problem the same way but would explain it differently?
- Did anyone solve the problem in a different way?
- Does anyone want to add on to _____’s strategy?
- Do you agree or disagree? Why?
Design Principle(s): Optimize output (for explanation)
2.2: Corresponding Parts (15 minutes)
Activity
This activity introduces important language students will apply to describe scaled copies. In particular, it introduces the important idea of corresponding parts. Students have previously analyzed corresponding sides in figures. Here they will begin to examine angles explicitly as well, understanding that corresponding angles in a figure and its scaled copy have the same measure.
Launch
Tell students that in this lesson, they will look more closely at copies of figures and describe specific parts in them.
Display the designs (the three images in the activity statement) and the following descriptions for all to see. Ask students what they notice and what they wonder. After discussion, explain that the original design and its two copies have parts that correspond to one another. Point out some of their corresponding parts:
- The X-pattern going across each figure
- The curved outline of each figure
- The points \(K\) in the original sign, \(A\) in Copy 1, and \(U\) in Copy 2
Arrange students in groups of 2 and provide access to their geometry toolkits (especially tracing paper). Give students 2–3 minutes to complete the first two questions and another 2 minutes to discuss their responses with their partner. Ask students to pause their work for a quick class discussion afterwards.
Have a few students name a set of corresponding points, segments, and angles.
Then, ask students to indicate whether they think either copy is a scaled copy. Invite a couple of students to share their reasoning. When the class reaches an agreement that Copy 1 is a scaled copy and Copy 2 is not, ask students to complete the remaining questions individually and to use tracing paper as a tool.
Consider demonstrating to the class how to use tracing paper to compare angles. Tell or show students that the line segments forming an angle could be extended for easier tracing and comparison.
For classrooms using the digital version of the activity, the applet has a moveable angle tool to compare the angles in the copies with the angles in the original.
Supports accessibility for: Memory; Language
Design Principle(s): Optimize output (for explanation)
Student Facing
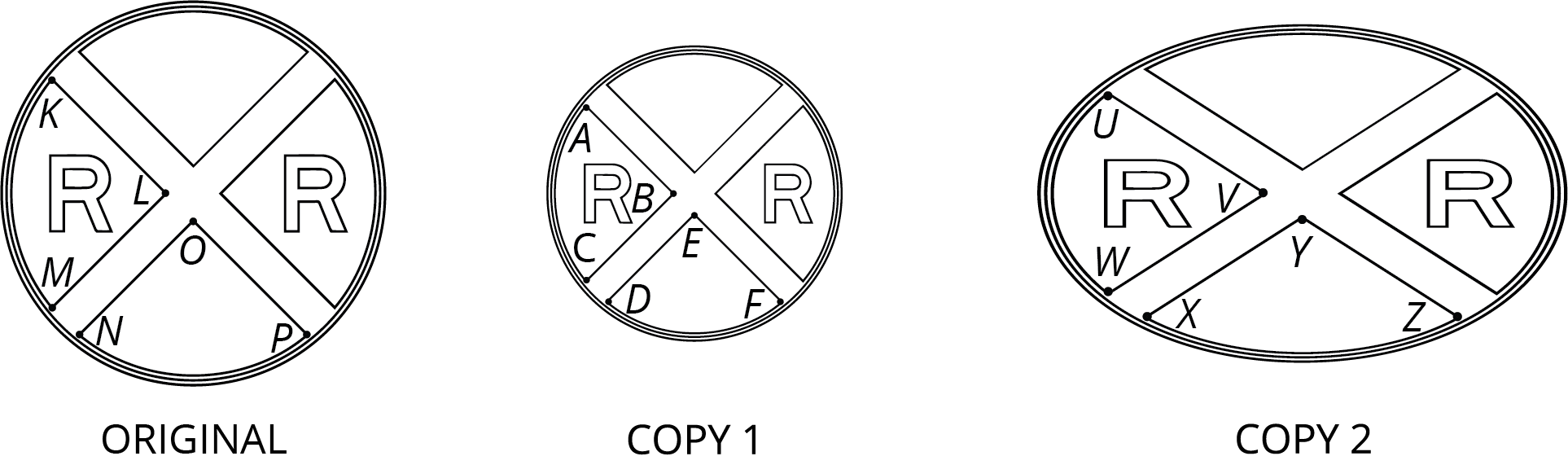
One road sign for railroad crossings is a circle with a large X in the middle and two R’s—with one on each side. Here is a picture with some points labeled and two copies of the picture. Drag and turn the moveable angle tool to compare the angles in the copies with the angles in the original.
- Complete this table to show corresponding parts in the three pictures.
original Copy 1 Copy 2 point \(L\) segment \(LM\) segment \(ED\) point \(X\) angle \(KLM\) angle \(XYZ\) - Is either copy a scaled copy of the original road sign? Explain your reasoning.
- Use the moveable angle tool to compare angle \(KLM\) with its corresponding angles in Copy 1 and Copy 2. What do you notice?
- Use the moveable angle tool to compare angle \(NOP\) with its corresponding angles in Copy 1 and Copy 2. What do you notice?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Tell students that in this lesson, they will look more closely at copies of figures and describe specific parts in them.
Display the designs (the three images in the activity statement) and the following descriptions for all to see. Ask students what they notice and what they wonder. After discussion, explain that the original design and its two copies have parts that correspond to one another. Point out some of their corresponding parts:
- The X-pattern going across each figure
- The curved outline of each figure
- The points \(K\) in the original sign, \(A\) in Copy 1, and \(U\) in Copy 2
Arrange students in groups of 2 and provide access to their geometry toolkits (especially tracing paper). Give students 2–3 minutes to complete the first two questions and another 2 minutes to discuss their responses with their partner. Ask students to pause their work for a quick class discussion afterwards.
Have a few students name a set of corresponding points, segments, and angles.
Then, ask students to indicate whether they think either copy is a scaled copy. Invite a couple of students to share their reasoning. When the class reaches an agreement that Copy 1 is a scaled copy and Copy 2 is not, ask students to complete the remaining questions individually and to use tracing paper as a tool.
Consider demonstrating to the class how to use tracing paper to compare angles. Tell or show students that the line segments forming an angle could be extended for easier tracing and comparison.
For classrooms using the digital version of the activity, the applet has a moveable angle tool to compare the angles in the copies with the angles in the original.
Supports accessibility for: Memory; Language
Design Principle(s): Optimize output (for explanation)
Student Facing
Here is a figure and two copies, each with some points labeled.
-
Complete this table to show corresponding parts in the three figures.
original copy 1 copy 2 point \(P\) segment \(LM\) segment \(EF\) point \(W\) angle \(KLM\) angle \(XYZ\) - Is either copy a scaled copy of the original figure? Explain your reasoning.
- Use tracing paper to compare angle \(KLM\) with its corresponding angles in Copy 1 and Copy 2. What do you notice?
- Use tracing paper to compare angle \(NOP\) with its corresponding angles in Copy 1 and Copy 2. What do you notice?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select a few students to share their observations about angles. Discuss the size of corresponding angles in figures that are scaled copies and those that are not. Ask questions such as:
- In the scaled copy, Copy 1, did the size of any angle change compared to its corresponding angle in the original sign? (No)
- In Copy 2, did the size of any angle change relative to its corresponding angle in the original sign? (Yes) Which ones? (Angle \(UVW\) has a different measure than angle \(KLM\), for example.)
- What can you say about corresponding angles in two figures that are scaled copies of one another? (They have the same measure.)
- What can you say about corresponding angles in two figures that are not scaled copies? (They might not have the same measure.)
2.3: Scaled Triangles (15 minutes)
Activity
In this activity, students continue to practice identifying corresponding parts of scaled copies. By organizing corresponding lengths in a table, students see that there is a single factor that relates each length in the original triangle to its corresponding length in a copy (MP8). They learn that this number is called a scale factor.
As students work on the first question, listen to how they reason about which triangles are scaled copies. Identify groups who use side lengths and angles as the basis for deciding. (Students are not expected to reason formally yet, but should begin to look to lengths and angles for clues.)
As students identify corresponding sides and their measures in the second and third questions, look out for confusion about corresponding parts. Notice how students decide which sides of the right triangles correspond.
If students still have access to tracing paper, monitor for students who use this tool strategically (MP5).
Launch
Arrange students into groups of 4. Assign each student one of the following pairs of triangles in the first question.
- A and E
- B and F
- C and G
- D and H
Give students 2 minutes of quiet think time to determine if their assigned triangles are scaled copies of the original triangle. Give another 2–3 minutes to discuss their responses and complete the first question in groups.
Discuss briefly as a class which triangles are scaled copies and select a couple of groups who reasoned in terms of lengths and angles to explain their reasoning. Some guiding questions:
- What information did you use to tell scaled copies from those that are not?
- How were you able to tell right away that some figures are not scaled copies?
Give students quiet work time to complete the rest of the task after the class recognizes that A, C, F, and H are not scaled copies.
Student Facing
Here is Triangle O, followed by a number of other triangles.

Your teacher will assign you two of the triangles to look at.
- For each of your assigned triangles, is it a scaled copy of Triangle O? Be prepared to explain your reasoning.
- As a group, identify all the scaled copies of Triangle O in the collection. Discuss your thinking. If you disagree, work to reach an agreement.
- List all the triangles that are scaled copies in the table. Record the side lengths that correspond to the side lengths of Triangle O listed in each column.
Triangle O 3 4 5 - Explain or show how each copy has been scaled from the original (Triangle O).
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Choose one of the triangles that is not a scaled copy of Triangle O. Describe how you could change at least one side to make a scaled copy, while leaving at least one side unchanged.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think that Triangle F is a scaled copy because just like the 3-4-5 triangle, the sides are also three consecutive whole numbers. Point out that corresponding angles are not equal.
Activity Synthesis
Display the image of all triangles and invite a couple of students to share how they knew which sides of the triangles correspond. Then, display a completed table in the third question for all to see. Ask each group to present its observations about one triangle and how the triangle has been scaled from the original. Encourage the use of “corresponding” in their explanations. As students present, record or illustrate their reasoning on the table, e.g., by drawing arrows between rows and annotating with the operation students are describing, as shown here.

Use the language that students use to describe the side lengths and the numerical relationships in the table to guide students toward scale factor. For example: “You explained that the lengths in Triangle F are all twice those in the original triangle, so we can write those as “2 times” the original numbers. Lengths in Triangle A are half of those in the original; we can write “\(\frac12\) times” the original numbers. We call those multipliers—the 2 and the \(\frac12\)-scale factors. We say that scaling Triangle O by a scale factor of 2 produces Triangle F, and that scaling Triangle O by \(\frac12\) produces Triangle A.”
Lesson Synthesis
Lesson Synthesis
- What do we mean by corresponding parts?
- What is a scale factor? How does it work?
Students can use informal language to describe corresponding parts, and recognize a scale factor as a common ratio between the lengths of corresponding side lengths. In the figure, triangle \(DEF\) is a scaled copy of triangle \(ABC\). We call parts that have the same position within each figure corresponding parts. For example, we refer to vertex \(E\) in triangle \(DEF\) and vertex \(B\) in triangle \(ABC\) as corresponding points; segment \(BC\) and segment \(EF\) as corresponding segments; and angle \(C\) (or angle \(BCA\)) and angle \(F\) (or angle \(EFD\)) as corresponding angles.
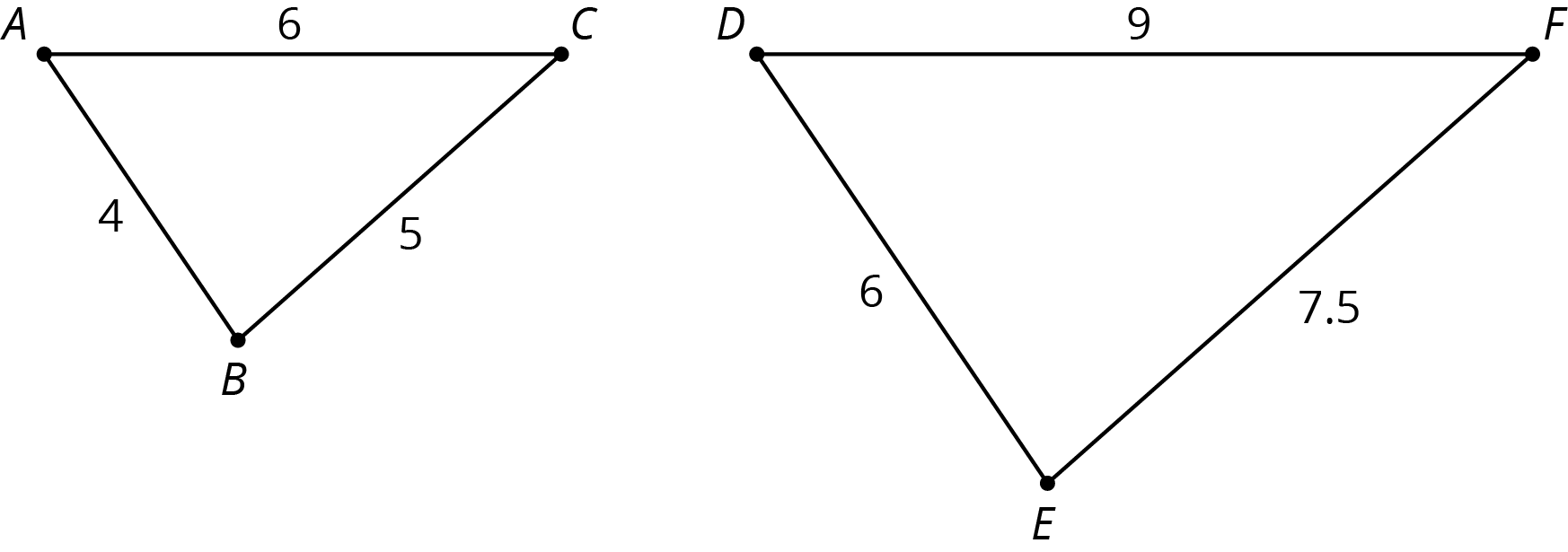
The segments in a scaled copy are always a certain number of times as long as the corresponding segments in the original figure. We call that number the scale factor. For example, the scale factor between \(ABC\) and its copy triangle \(DEF\) is \(\frac32\) or 1.5 because all lengths in triangle \(DEF\) are 1.5 times as long as the corresponding lengths in triangle \(ABC\).
2.4: Cool-down - Comparing Polygons $ABCD$ and $PQRS$ (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
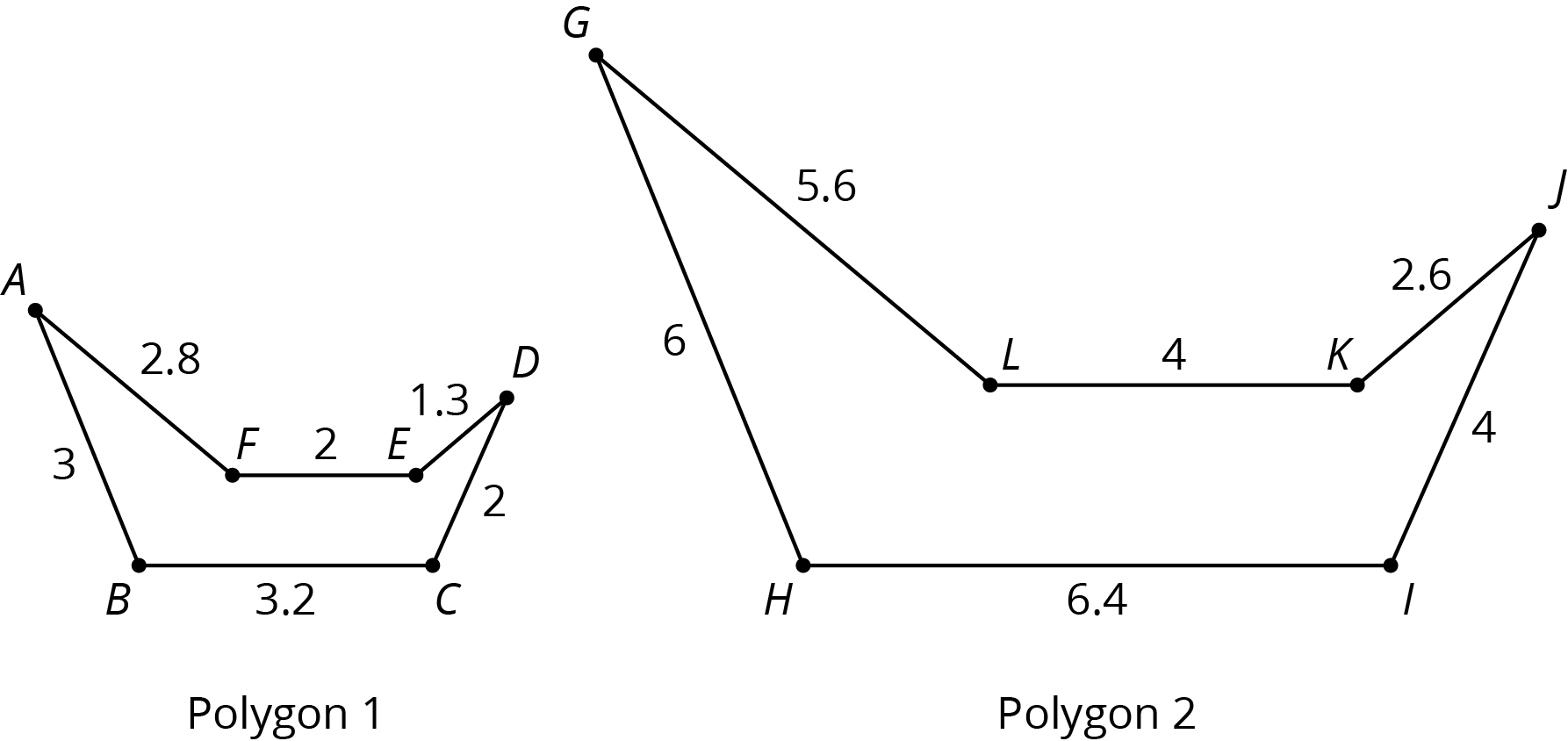
A figure and its scaled copy have corresponding parts, or parts that are in the same position in relation to the rest of each figure. These parts could be points, segments, or angles. For example, Polygon 2 is a scaled copy of Polygon 1.
-
Each point in Polygon 1 has a corresponding point in Polygon 2.
For example, point \(B\) corresponds to point \(H\) and point \(C\) corresponds to point \(I\). -
Each segment in Polygon 1 has a corresponding segment in Polygon 2.
For example, segment \(AF\) corresponds to segment \(GL\). -
Each angle in Polygon 1 also has a corresponding angle in Polygon 2.
For example, angle \(DEF\) corresponds to angle \(JKL\).
The scale factor between Polygon 1 and Polygon 2 is 2, because all of the lengths in Polygon 2 are 2 times the corresponding lengths in Polygon 1. The angle measures in Polygon 2 are the same as the corresponding angle measures in Polygon 1. For example, the measure of angle \(JKL\) is the same as the measure of angle \(DEF\).