Lesson 4
Scaled Relationships
4.1: Three Quadrilaterals (Part 1) (5 minutes)
Warm-up
This warm-up gives students a chance to practice identifying corresponding angles of scaled copies, measure angles using a protractor, and test their earlier conjecture that corresponding angles have the same measure.
Launch
Have students look at the figures in the activity, and ask “What do you notice? What do you wonder?” Call out in particular questions about the angles in the figures (e.g., whether corresponding ones have the same measure). Tell students that they will test their previous observation about the angles of scaled figures, this time by using protractors instead of tracing paper.
Provide access to protractors. Clear protractors with no holes and with radial lines printed on them are recommended here. Some angles may be challenging to measure because of the size of the polygons. If students find the sides of a polygon not long enough to accommodate angle measurements, suggest that they extend the lines, or demonstrate how to do so (especially if available protractors are opaque with holes in the middle).
Student Facing
Each of these polygons is a scaled copy of the others.

- Name two pairs of corresponding angles. What can you say about the sizes of these angles?
- Check your prediction by measuring at least one pair of corresponding angles using a protractor. Record your measurements to the nearest \(5^\circ\).
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may read the wrong number on the protractor, moving down from the \(180^\circ\) mark instead of up from the \(0^\circ\) mark, or reading the measurement outside of one of the lines forming the angle instead of between the two lines. Clarify the angle being measured, how to line up the protractor, or how to read the markings correctly.
Activity Synthesis
Select a few students to share their angle measurements and poll the class briefly for agreement and disagreement. Discuss major discrepancies, if any. Students should be able to confirm that all corresponding angles in the scaled polygons are equal.
If desired, ask students whether recording the angles to the nearest 1 degree would be appropriate: in general, the thickness of the line segments and the markings on the protractor limit accuracy, so reporting to the nearest 5 degrees is appropriate (as long as none of the angles are too close to halfway between two increments).
4.2: Three Quadrilaterals (Part 2) (10 minutes)
Activity
Students have seen that the lengths of corresponding segments in a figure and its scaled copy vary by the same scale factor. Here, they learn that in such a pair of figures, any corresponding distances—not limited to lengths of sides or segments—are related by the same scale factor. The side lengths of the polygons in this task cannot be easily determined, so students must look to other distances to compare.
Students must take care when they identify corresponding vertices and distances. As students work, urge them to attend to the order in which points or segments are listed.
If students are not sure what to make out of the values in the table (for the second question), encourage them to consider the corresponding distances of two figures at a time. For example, ask: What do you notice about the corresponding vertical distances in \(IJKL\) and \(EFGH\)? What about the corresponding horizontal distances in those two figures?
Launch
Arrange students in groups of 2. Ask if they can tell the lengths of segments \(GF\) or \(DC\) from the grid (without using rulers). Explain that they will explore another way to compare length measurements in scaled copies.
Give students 2–3 minutes of quiet work time for the first two questions, and 1 minute to discuss their responses with a partner before continuing on to the last question.
Student Facing
Each of these polygons is a scaled copy of the others. You already checked their corresponding angles.

- The side lengths of the polygons are hard to tell from the grid, but there are other corresponding distances that are easier to compare. Identify the distances in the other two polygons that correspond to \(DB\) and \(AC\), and record them in the table.
quadrilateral distance that
corresponds to \(DB\)distance that
corresponds to \(AC\)\(ABCD\) \(DB = 4\) \(AC = 6\) \(EFGH\) \(IJKL\) -
Look at the values in the table. What do you notice?
Pause here so your teacher can review your work.
-
The larger figure is a scaled copy of the smaller figure.
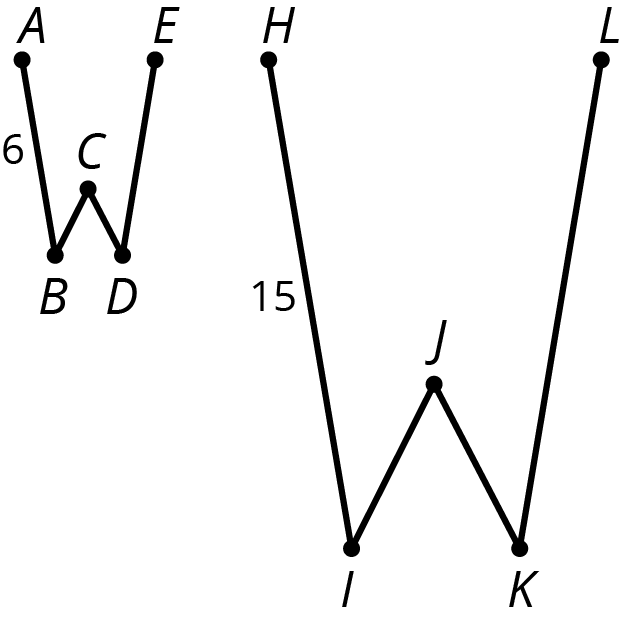
- If \(AE = 4\), how long is the corresponding distance in the second figure? Explain or show your reasoning.
- If \(IK = 5\), how long is the corresponding distance in the first figure? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may list the corresponding vertices for distances in the wrong order. For example, instead of writing \(IK\) as the distance corresponding to \(DB\), they may write \(KI\). Remind students of the corresponding points by asking, “Which vertex in \(IJKL\) corresponds to \(D\)? Which corresponds to \(B\)?” and have them match the order of the vertices accordingly.
Activity Synthesis
Display the completed tables for all to see. To highlight how all distances in a scaled copy (not just the side lengths of the figure) are related by the same scale factor, discuss:
- How does the vertical distance in \(ABCD\) compare to that in \(EFGH\)? How do the horizontal distances in the two polygons compare? Do the pairs of vertical and horizontal distances share the same scale factor?
- How do the vertical distances in \(EFGH\) and \(IJKL\) compare? What about the horizontal distances? Is there a common scale factor? What is that scale factor?
- What scale factor relates the corresponding lengths and distances in the two drawings of the letter W?
Supports accessibility for: Visual-spatial processing
Design Principle(s): Maximize meta-awareness
4.3: Scaled or Not Scaled? (10 minutes)
Activity
The purpose of this activity is for students to determine that figures are not scaled copies, even though they have either corresponding angles with equal measures or corresponding distances multiplied by the same scale factor. This shows that to determine one figure is a scaled copy of another, we have to check both the corresponding angles and the corresponding distances.
As students work, monitor for convincing arguments about why one polygon is or is not a scaled copy of the other. Ask them to present their cases during the whole-class discussion. As they present and analyze different arguments about the figures in the discussion, students will engage in MP3.
Launch
Keep students in the same groups. Provide access to geometry toolkits. Give students 6–7 minutes of quiet work time.
Supports accessibility for: Organization; Attention
Student Facing
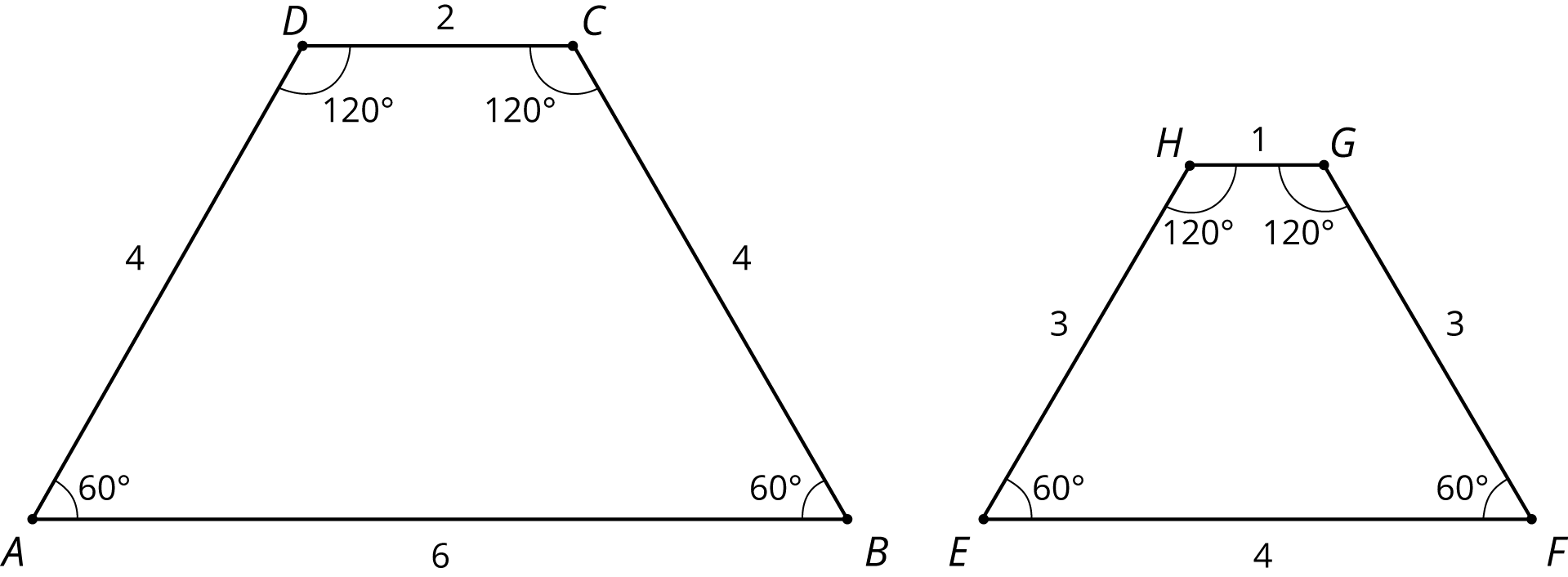
Here are two quadrilaterals.

- Mai says that Polygon \(ZSCH\) is a scaled copy of Polygon \(XJYN\), but Noah disagrees. Do you agree with either of them? Explain or show your reasoning.
- Record the corresponding distances in the table. What do you notice?
quadrilateral horizontal distance vertical distance \(XJYN\) \(XY = \phantom{33}\) \(JN = \phantom{33}\) \(ZSCH\) \(ZC = \phantom{33}\) \(SH = \phantom{33}\) - Measure at least three pairs of corresponding angles in \(XJYN\) and \(ZSCH\) using a protractor. Record your measurements to the nearest \(5^\circ\). What do you notice?
- Do these results change your answer to the first question? Explain.
-
Here are two more quadrilaterals.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
All side lengths of quadrilateral \(MNOP\) are 2, and all side lengths of quadrilateral \(QRST\) are 3. Does \(MNOP\) have to be a scaled copy of \(QRST\)? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may rely on the appearance of the figures rather than analyze given information to draw conclusions about scaling. Urge them to look for information about distances and angles (and to think about which tools could help them find such information) to support their argument.
Some students may struggle with comparing the corresponding angles in the first pair of figures. Remind students of the tools that are at their disposal, and that they could extend the sides of the polygons, if needed, to make it easier to measure the angles.
Activity Synthesis
The goal of this discussion is to make clear that angle measurements and distances are both important when deciding whether two polygons are scaled copies. To highlight the different arguments about whether one polygon is a scaled copy of another, consider debriefing with a role play. Ask four students to take on the roles of the four characters—Mai and Noah in the first question, and Kiran and Lin in the second—and make a brief argument about why they believe one figure is a scaled copy of the other in each case. Poll the class after each pair of cases are presented and find out with whom students agree.
Design Principle(s): Optimize output (for explanation)
4.4: Comparing Pictures of Birds (10 minutes)
Optional activity
In this activity, students use what they know about corresponding lengths and angles to show that one picture of a bird is not a scaled copy of the other. Unlike in previous tasks, minimal scaffolding is given here, so students need to decide what evidence is necessary to explain or show an absence of scaling. As students work, notice the different ways students use corresponding lengths and angles to think about scaling.
Identifying a specific measurement in one image and the corresponding measurements in the other (which show that one is not a scaled copy of the other) requires thinking about the structure of the pictures (MP7).
Monitor students for different approaches to show that one image is not a scaled copy of the other:
- Identifying corresponding angles in the two images which have different measures
- Identifying two pair of corresponding segments in the images with different scale factors
Select students who use these methods and ask them to present their approaches, in this sequence, during the discussion.
Launch
Arrange students in groups of 3–4. Provide access to geometry toolkits.
Give students 2 minutes of quiet work time followed by 1–2 minutes to discuss in groups how to find evidence that one picture is not a scaled copy of the other. Then, briefly discuss students’ ideas as a class. Consider listing the ideas for all to see and discussing which ones are likely to be most effective.
If students' ideas deviate from drawing corresponding points and segments and comparing distances and angles, guide them with some prompts. For example:
- Pick a point that can be easily referenced (e.g., the tip of one wing) on one picture. Ask for the corresponding point on the other.
- Ask if that pair of corresponding points could help them determine if one picture is scaled from the other. If not, ask what else might be needed.
- Add another point and a segment connecting the two points. Ask if or how the segment could help, and so on.
Student Facing
Here are two pictures of a bird. Find evidence that one picture is not a scaled copy of the other. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 3–4. Provide access to geometry toolkits.
Give students 2 minutes of quiet work time followed by 1–2 minutes to discuss in groups how to find evidence that one picture is not a scaled copy of the other. Then, briefly discuss students’ ideas as a class. Consider listing the ideas for all to see and discussing which ones are likely to be most effective.
If students' ideas deviate from drawing corresponding points and segments and comparing distances and angles, guide them with some prompts. For example:
- Pick a point that can be easily referenced (e.g., the tip of one wing) on one picture. Ask for the corresponding point on the other.
- Ask if that pair of corresponding points could help them determine if one picture is scaled from the other. If not, ask what else might be needed.
- Add another point and a segment connecting the two points. Ask if or how the segment could help, and so on.
Student Facing
Here are two pictures of a bird. Find evidence that one picture is not a scaled copy of the other. Be prepared to explain your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may draw two segments that do not share a point, or choose non-corresponding points and segments on the two figures. Refer students to earlier work involving polygons and point out pairs of distances that could be used for comparison and those that could not be. Remind them that we can only compare the corresponding parts, not just any two parts.
Activity Synthesis
Invite select students to share their reasoning. Ask how they knew that certain pairs of points in the images were corresponding points. Students could identify a unique feature such as the eyes or the tip of the wing. Make sure students understand that:
- Corresponding angles on an image and a scaled copy have the same measure
- Corresponding segments on an image and a scaled copy are related by the same scale factor
To conclude that an image is not a scaled copy of another, it is sufficient to find one pair of corresponding angle measures that are different or two pairs of corresponding segments with different scale factors.
Design Principle(s): Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
- Does a scale factor affect any other measurements other than segment lengths?
- How can we be sure that a figure is a scaled copy? What features do we check?
When a scaled copy is created from a figure, we know that:
- The distances between any two points in the original figure, even those not connected by segments, are scaled by the same scale factor.
- The corresponding angles in the original figure and scaled copies are congruent.
Polygons are a perfect context in which to apply these two ideas, being made up of line segments meeting at angles. So we can use these observations to check whether a polygon is actually a scaled copy of another. If all the corresponding angles are the same size and all corresponding distances are all scaled by the same factor, then we can conclude that it is a scaled copy of the other.
4.5: Cool-down - Corresponding Polygons (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When a figure is a scaled copy of another figure, we know that:
-
All distances in the copy can be found by multiplying the corresponding distances in the original figure by the same scale factor, whether or not the endpoints are connected by a segment.
For example, Polygon \(STUVWX\) is a scaled copy of Polygon \(ABCDEF\). The scale factor is 3. The distance from \(T\) to \(X\) is 6, which is three times the distance from \(B\) to \(F\).

- All angles in the copy have the same measure as the corresponding angles in the original figure, as in these triangles.
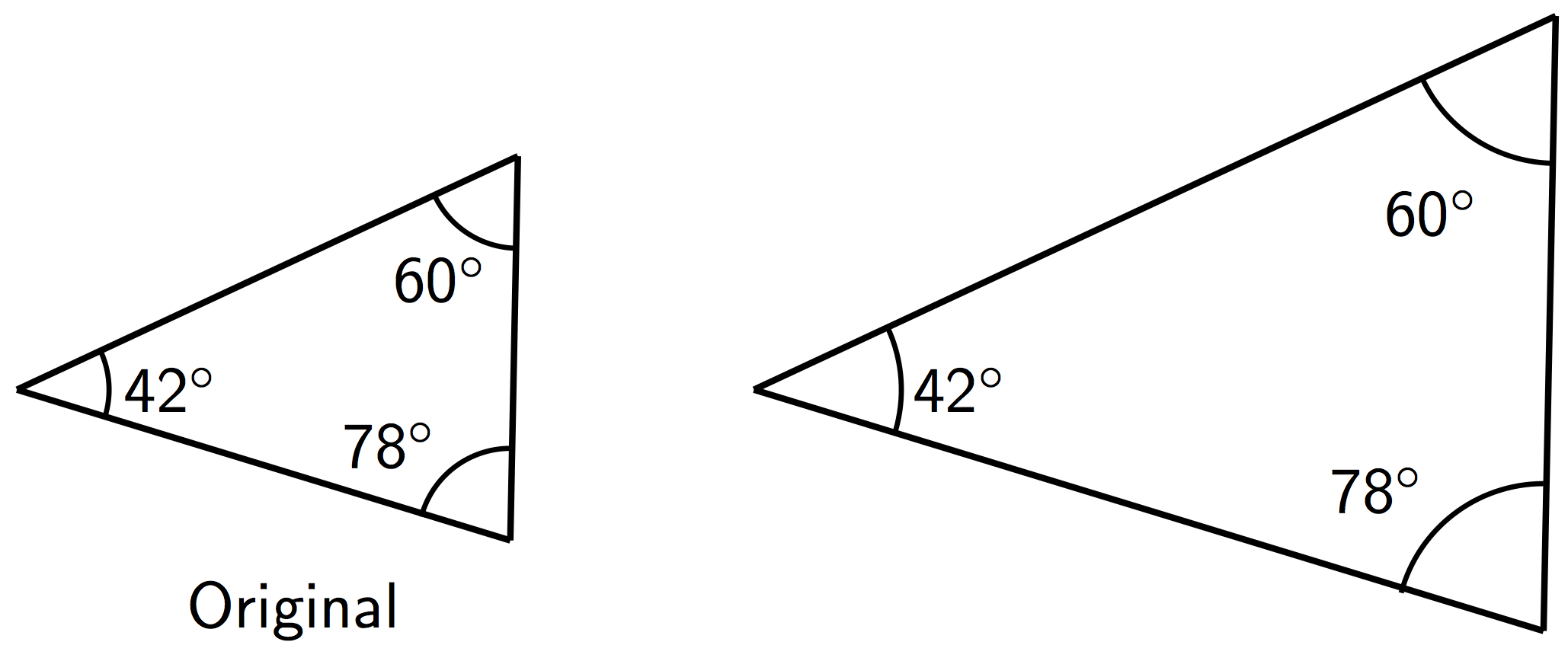
These observations can help explain why one figure is not a scaled copy of another.
For example, even though their corresponding angles have the same measure, the second rectangle is not a scaled copy of the first rectangle, because different pairs of corresponding lengths have different scale factors, \(2 \boldcdot \frac12 = 1\) but \(3 \boldcdot \frac23 = 2\).
